On the Relevance of Byzantine Robust Optimization Against Data Poisoning

The success of machine learning (ML) has been intimately linked with the availability of large amounts of data, typically collected from heterogeneous sources and processed on vast networks of computing devices (also called {\em workers}). Beyond accuracy, the use of ML in critical domains such as healthcare and autonomous driving calls for robustness against {\em data poisoning}and some {\em faulty workers}. The problem of {\em Byzantine ML} formalizes these robustness issues by considering a distributed ML environment in which workers (storing a portion of the global dataset) can deviate arbitrarily from the prescribed algorithm. Although the problem has attracted a lot of attention from a theoretical point of view, its practical importance for addressing realistic faults (where the behavior of any worker is locally constrained) remains unclear. It has been argued that the seemingly weaker threat model where only workers' local datasets get poisoned is more reasonable. We prove that, while tolerating a wider range of faulty behaviors, Byzantine ML yields solutions that are, in a precise sense, optimal even under the weaker data poisoning threat model. Then, we study a generic data poisoning model wherein some workers have {\em fully-poisonous local data}, i.e., their datasets are entirely corruptible, and the remainders have {\em partially-poisonous local data}, i.e., only a fraction of their local datasets is corruptible. We prove that Byzantine-robust schemes yield optimal solutions against both these forms of data poisoning, and that the former is more harmful when workers have {\em heterogeneous} local data.

Tackling Byzantine Clients in Federated Learning

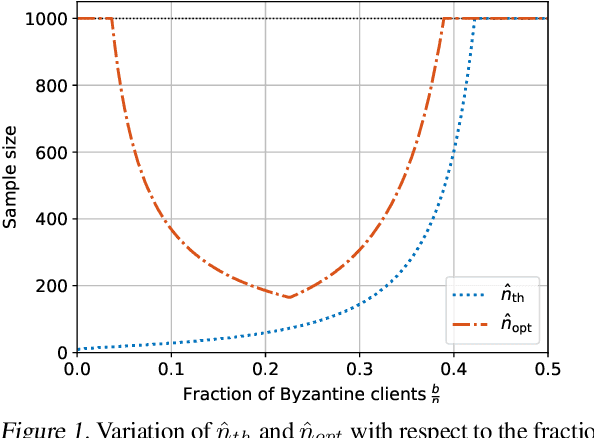
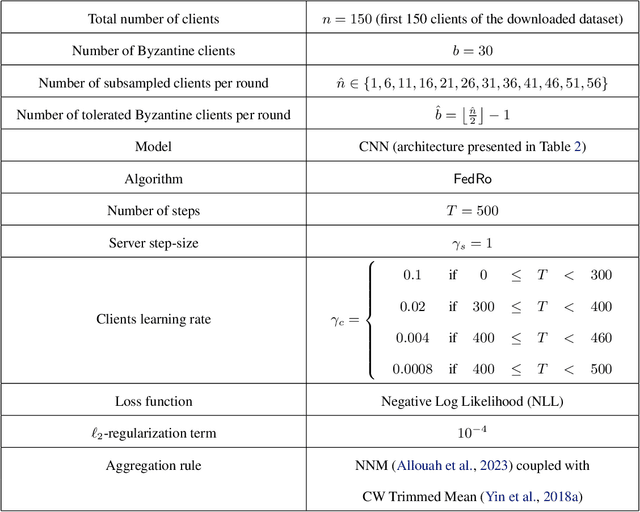
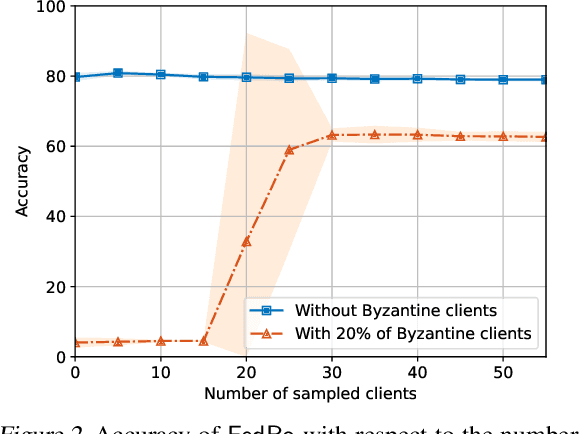
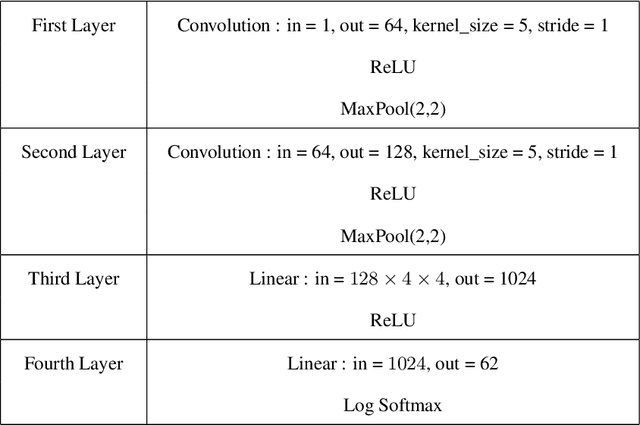
The possibility of adversarial (a.k.a., {\em Byzantine}) clients makes federated learning (FL) prone to arbitrary manipulation. The natural approach to robustify FL against adversarial clients is to replace the simple averaging operation at the server in the standard $\mathsf{FedAvg}$ algorithm by a \emph{robust averaging rule}. While a significant amount of work has been devoted to studying the convergence of federated {\em robust averaging} (which we denote by $\mathsf{FedRo}$), prior work has largely ignored the impact of {\em client subsampling} and {\em local steps}, two fundamental FL characteristics. While client subsampling increases the effective fraction of Byzantine clients, local steps increase the drift between the local updates computed by honest (i.e., non-Byzantine) clients. Consequently, a careless deployment of $\mathsf{FedRo}$ could yield poor performance. We validate this observation by presenting an in-depth analysis of $\mathsf{FedRo}$ tightly analyzing the impact of client subsampling and local steps. Specifically, we present a sufficient condition on client subsampling for nearly-optimal convergence of $\mathsf{FedRo}$ (for smooth non-convex loss). Also, we show that the rate of improvement in learning accuracy {\em diminishes} with respect to the number of clients subsampled, as soon as the sample size exceeds a threshold value. Interestingly, we also observe that under a careful choice of step-sizes, the learning error due to Byzantine clients decreases with the number of local steps. We validate our theory by experiments on the FEMNIST and CIFAR-$10$ image classification tasks.

Epidemic Learning: Boosting Decentralized Learning with Randomized Communication

We present Epidemic Learning (EL), a simple yet powerful decentralized learning (DL) algorithm that leverages changing communication topologies to achieve faster model convergence compared to conventional DL approaches. At each round of EL, each node sends its model updates to a random sample of $s$ other nodes (in a system of $n$ nodes). We provide an extensive theoretical analysis of EL, demonstrating that its changing topology culminates in superior convergence properties compared to the state-of-the-art (static and dynamic) topologies. Considering smooth non-convex loss functions, the number of transient iterations for EL, i.e., the rounds required to achieve asymptotic linear speedup, is in $\mathcal{O}(\frac{n^3}{s^2})$ which outperforms the best-known bound $\mathcal{O}({n^3})$ by a factor of $ s^2 $, indicating the benefit of randomized communication for DL. We empirically evaluate EL in a 96-node network and compare its performance with state-of-the-art DL approaches. Our results illustrate that EL converges up to $ 1.6\times $ quicker than baseline DL algorithms and attains 1.8% higher accuracy for the same communication volume.

Fixing by Mixing: A Recipe for Optimal Byzantine ML under Heterogeneity

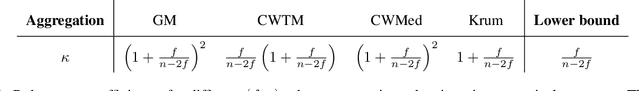
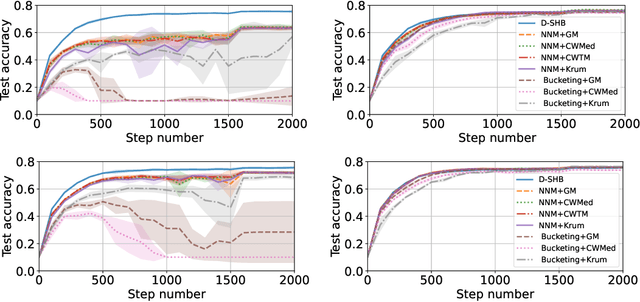
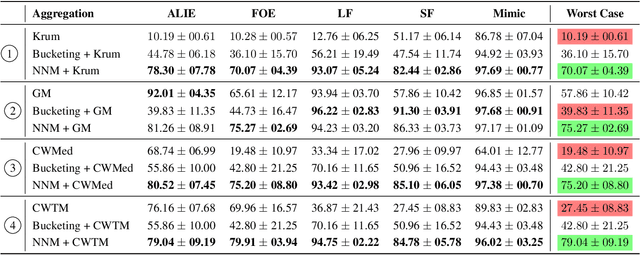
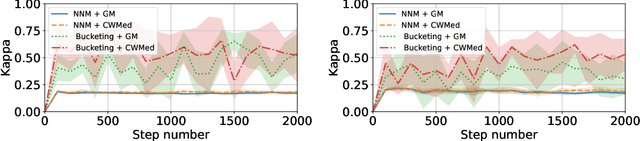
Byzantine machine learning (ML) aims to ensure the resilience of distributed learning algorithms to misbehaving (or Byzantine) machines. Although this problem received significant attention, prior works often assume the data held by the machines to be homogeneous, which is seldom true in practical settings. Data heterogeneity makes Byzantine ML considerably more challenging, since a Byzantine machine can hardly be distinguished from a non-Byzantine outlier. A few solutions have been proposed to tackle this issue, but these provide suboptimal probabilistic guarantees and fare poorly in practice. This paper closes the theoretical gap, achieving optimality and inducing good empirical results. In fact, we show how to automatically adapt existing solutions for (homogeneous) Byzantine ML to the heterogeneous setting through a powerful mechanism, we call nearest neighbor mixing (NNM), which boosts any standard robust distributed gradient descent variant to yield optimal Byzantine resilience under heterogeneity. We obtain similar guarantees (in expectation) by plugging NNM in the distributed stochastic heavy ball method, a practical substitute to distributed gradient descent. We obtain empirical results that significantly outperform state-of-the-art Byzantine ML solutions.

SoK: On the Impossible Security of Very Large Foundation Models

Large machine learning models, or so-called foundation models, aim to serve as base-models for application-oriented machine learning. Although these models showcase impressive performance, they have been empirically found to pose serious security and privacy issues. We may however wonder if this is a limitation of the current models, or if these issues stem from a fundamental intrinsic impossibility of the foundation model learning problem itself. This paper aims to systematize our knowledge supporting the latter. More precisely, we identify several key features of today's foundation model learning problem which, given the current understanding in adversarial machine learning, suggest incompatibility of high accuracy with both security and privacy. We begin by observing that high accuracy seems to require (1) very high-dimensional models and (2) huge amounts of data that can only be procured through user-generated datasets. Moreover, such data is fundamentally heterogeneous, as users generally have very specific (easily identifiable) data-generating habits. More importantly, users' data is filled with highly sensitive information, and maybe heavily polluted by fake users. We then survey lower bounds on accuracy in privacy-preserving and Byzantine-resilient heterogeneous learning that, we argue, constitute a compelling case against the possibility of designing a secure and privacy-preserving high-accuracy foundation model. We further stress that our analysis also applies to other high-stake machine learning applications, including content recommendation. We conclude by calling for measures to prioritize security and privacy, and to slow down the race for ever larger models.

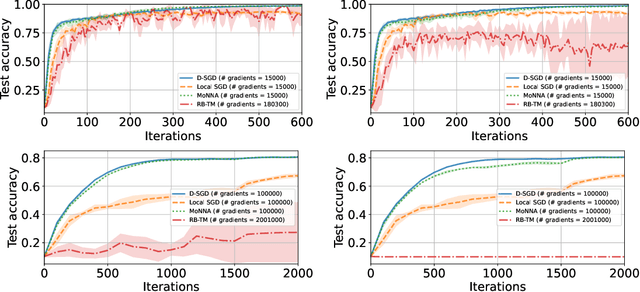
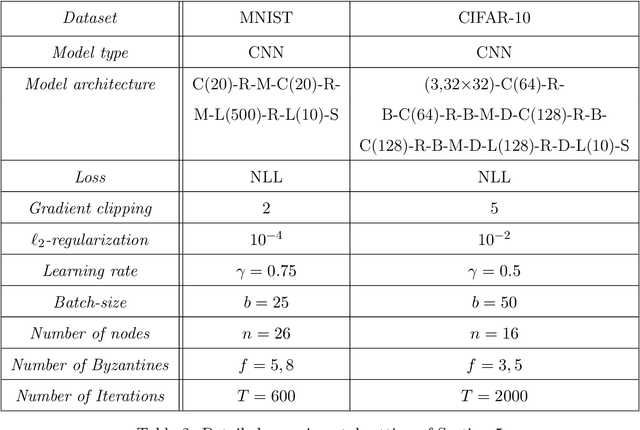
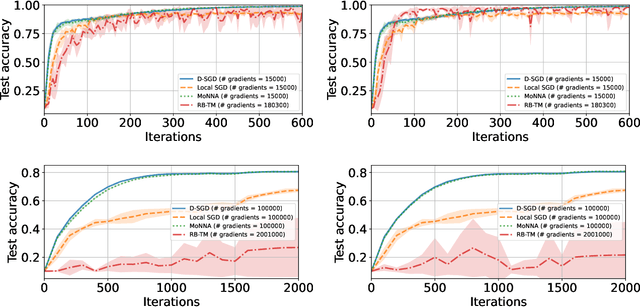
Making Byzantine Decentralized Learning Efficient

Decentralized-SGD (D-SGD) distributes heavy learning tasks across multiple machines (a.k.a., {\em nodes}), effectively dividing the workload per node by the size of the system. However, a handful of \emph{Byzantine} (i.e., misbehaving) nodes can jeopardize the entire learning procedure. This vulnerability is further amplified when the system is \emph{asynchronous}. Although approaches that confer Byzantine resilience to D-SGD have been proposed, these significantly impact the efficiency of the process to the point of even negating the benefit of decentralization. This naturally raises the question: \emph{can decentralized learning simultaneously enjoy Byzantine resilience and reduced workload per node?} We answer positively by proposing \newalgorithm{} that ensures Byzantine resilience without losing the computational efficiency of D-SGD. Essentially, \newalgorithm{} weakens the impact of Byzantine nodes by reducing the variance in local updates using \emph{Polyak's momentum}. Then, by establishing coordination between nodes via {\em signed echo broadcast} and a {\em nearest-neighbor averaging} scheme, we effectively tolerate Byzantine nodes whilst distributing the overhead amongst the non-Byzantine nodes. To demonstrate the correctness of our algorithm, we introduce and analyze a novel {\em Lyapunov function} that accounts for the {\em non-Markovian model drift} arising from the use of momentum. We also demonstrate the efficiency of \newalgorithm{} through experiments on several image classification tasks.

Byzantine Machine Learning Made Easy by Resilient Averaging of Momentums

Byzantine resilience emerged as a prominent topic within the distributed machine learning community. Essentially, the goal is to enhance distributed optimization algorithms, such as distributed SGD, in a way that guarantees convergence despite the presence of some misbehaving (a.k.a., {\em Byzantine}) workers. Although a myriad of techniques addressing the problem have been proposed, the field arguably rests on fragile foundations. These techniques are hard to prove correct and rely on assumptions that are (a) quite unrealistic, i.e., often violated in practice, and (b) heterogeneous, i.e., making it difficult to compare approaches. We present \emph{RESAM (RESilient Averaging of Momentums)}, a unified framework that makes it simple to establish optimal Byzantine resilience, relying only on standard machine learning assumptions. Our framework is mainly composed of two operators: \emph{resilient averaging} at the server and \emph{distributed momentum} at the workers. We prove a general theorem stating the convergence of distributed SGD under RESAM. Interestingly, demonstrating and comparing the convergence of many existing techniques become direct corollaries of our theorem, without resorting to stringent assumptions. We also present an empirical evaluation of the practical relevance of RESAM.

An Equivalence Between Data Poisoning and Byzantine Gradient Attacks

To study the resilience of distributed learning, the "Byzantine" literature considers a strong threat model where workers can report arbitrary gradients to the parameter server. Whereas this model helped obtain several fundamental results, it has sometimes been considered unrealistic, when the workers are mostly trustworthy machines. In this paper, we show a surprising equivalence between this model and data poisoning, a threat considered much more realistic. More specifically, we prove that every gradient attack can be reduced to data poisoning, in any personalized federated learning system with PAC guarantees (which we show are both desirable and realistic). This equivalence makes it possible to obtain new impossibility results on the resilience to data poisoning as corollaries of existing impossibility theorems on Byzantine machine learning. Moreover, using our equivalence, we derive a practical attack that we show (theoretically and empirically) can be very effective against classical personalized federated learning models.

Strategyproof Learning: Building Trustworthy User-Generated Datasets

Today's large-scale machine learning algorithms harness massive amounts of user-generated data to train large models. However, especially in the context of content recommendation with enormous social, economical and political incentives to promote specific views, products or ideologies, strategic users might be tempted to fabricate or mislabel data in order to bias algorithms in their favor. Unfortunately, today's learning schemes strongly incentivize such strategic data misreporting. This is a major concern, as it endangers the trustworthiness of the entire training datasets, and questions the safety of any algorithm trained on such datasets. In this paper, we show that, perhaps surprisingly, incentivizing data misreporting is not a fatality. We propose the first personalized collaborative learning framework, Licchavi, with provable strategyproofness guarantees through a careful design of the underlying loss function. Interestingly, we also prove that Licchavi is Byzantine resilient: it tolerates a minority of users that provide arbitrary data.