Revisiting Ensembling in One-Shot Federated Learning

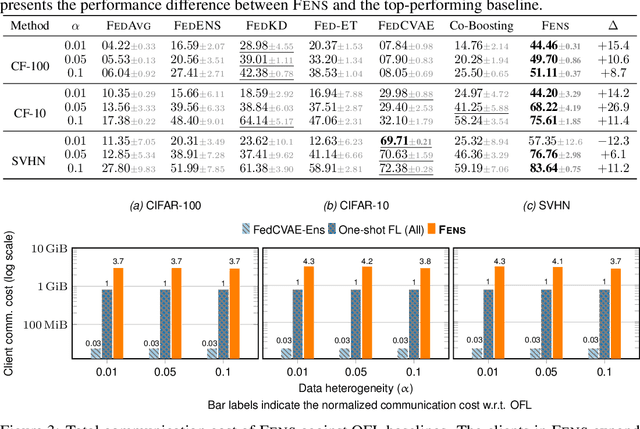
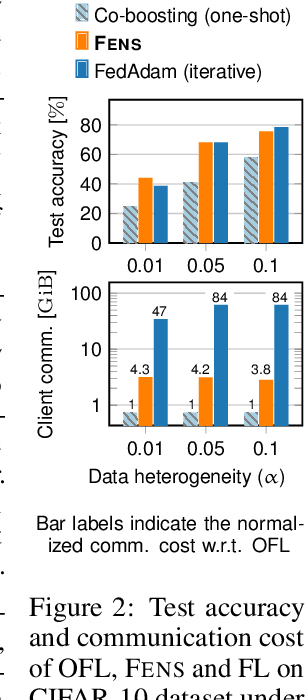
Federated learning (FL) is an appealing approach to training machine learning models without sharing raw data. However, standard FL algorithms are iterative and thus induce a significant communication cost. One-shot federated learning (OFL) trades the iterative exchange of models between clients and the server with a single round of communication, thereby saving substantially on communication costs. Not surprisingly, OFL exhibits a performance gap in terms of accuracy with respect to FL, especially under high data heterogeneity. We introduce FENS, a novel federated ensembling scheme that approaches the accuracy of FL with the communication efficiency of OFL. Learning in FENS proceeds in two phases: first, clients train models locally and send them to the server, similar to OFL; second, clients collaboratively train a lightweight prediction aggregator model using FL. We showcase the effectiveness of FENS through exhaustive experiments spanning several datasets and heterogeneity levels. In the particular case of heterogeneously distributed CIFAR-10 dataset, FENS achieves up to a 26.9% higher accuracy over state-of-the-art (SOTA) OFL, being only 3.1% lower than FL. At the same time, FENS incurs at most 4.3x more communication than OFL, whereas FL is at least 10.9x more communication-intensive than FENS.

Fine-Tuning Personalization in Federated Learning to Mitigate Adversarial Clients

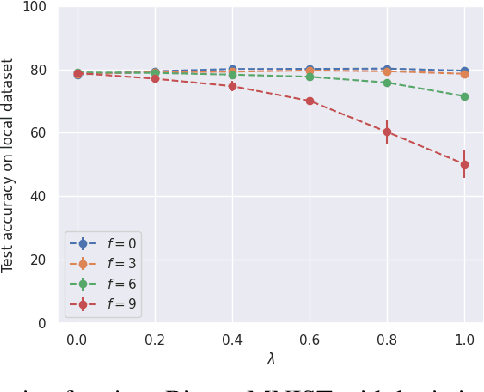
Federated learning (FL) is an appealing paradigm that allows a group of machines (a.k.a. clients) to learn collectively while keeping their data local. However, due to the heterogeneity between the clients' data distributions, the model obtained through the use of FL algorithms may perform poorly on some client's data. Personalization addresses this issue by enabling each client to have a different model tailored to their own data while simultaneously benefiting from the other clients' data. We consider an FL setting where some clients can be adversarial, and we derive conditions under which full collaboration fails. Specifically, we analyze the generalization performance of an interpolated personalized FL framework in the presence of adversarial clients, and we precisely characterize situations when full collaboration performs strictly worse than fine-tuned personalization. Our analysis determines how much we should scale down the level of collaboration, according to data heterogeneity and the tolerable fraction of adversarial clients. We support our findings with empirical results on mean estimation and binary classification problems, considering synthetic and benchmark image classification datasets.

Boosting Robustness by Clipping Gradients in Distributed Learning

Robust distributed learning consists in achieving good learning performance despite the presence of misbehaving workers. State-of-the-art (SOTA) robust distributed gradient descent (Robust-DGD) methods, relying on robust aggregation, have been proven to be optimal: Their learning error matches the lower bound established under the standard heterogeneity model of $(G, B)$-gradient dissimilarity. The learning guarantee of SOTA Robust-DGD cannot be further improved when model initialization is done arbitrarily. However, we show that it is possible to circumvent the lower bound, and improve the learning performance, when the workers' gradients at model initialization are assumed to be bounded. We prove this by proposing pre-aggregation clipping of workers' gradients, using a novel scheme called adaptive robust clipping (ARC). Incorporating ARC in Robust-DGD provably improves the learning, under the aforementioned assumption on model initialization. The factor of improvement is prominent when the tolerable fraction of misbehaving workers approaches the breakdown point. ARC induces this improvement by constricting the search space, while preserving the robustness property of the original aggregation scheme at the same time. We validate this theoretical finding through exhaustive experiments on benchmark image classification tasks.

On the Relevance of Byzantine Robust Optimization Against Data Poisoning

The success of machine learning (ML) has been intimately linked with the availability of large amounts of data, typically collected from heterogeneous sources and processed on vast networks of computing devices (also called {\em workers}). Beyond accuracy, the use of ML in critical domains such as healthcare and autonomous driving calls for robustness against {\em data poisoning}and some {\em faulty workers}. The problem of {\em Byzantine ML} formalizes these robustness issues by considering a distributed ML environment in which workers (storing a portion of the global dataset) can deviate arbitrarily from the prescribed algorithm. Although the problem has attracted a lot of attention from a theoretical point of view, its practical importance for addressing realistic faults (where the behavior of any worker is locally constrained) remains unclear. It has been argued that the seemingly weaker threat model where only workers' local datasets get poisoned is more reasonable. We prove that, while tolerating a wider range of faulty behaviors, Byzantine ML yields solutions that are, in a precise sense, optimal even under the weaker data poisoning threat model. Then, we study a generic data poisoning model wherein some workers have {\em fully-poisonous local data}, i.e., their datasets are entirely corruptible, and the remainders have {\em partially-poisonous local data}, i.e., only a fraction of their local datasets is corruptible. We prove that Byzantine-robust schemes yield optimal solutions against both these forms of data poisoning, and that the former is more harmful when workers have {\em heterogeneous} local data.

Tackling Byzantine Clients in Federated Learning

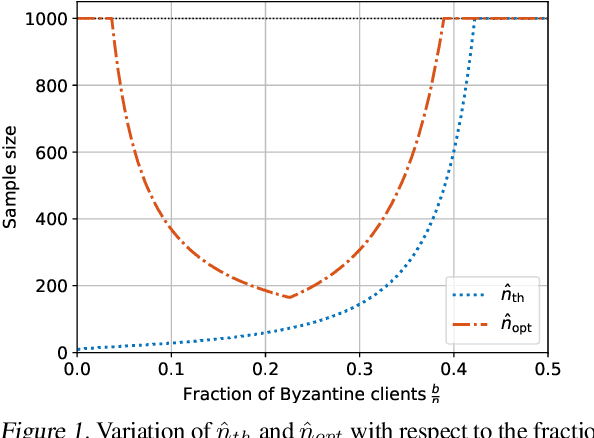
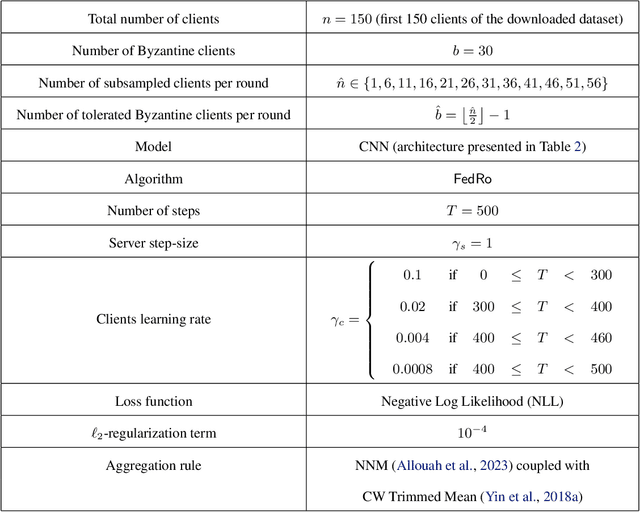
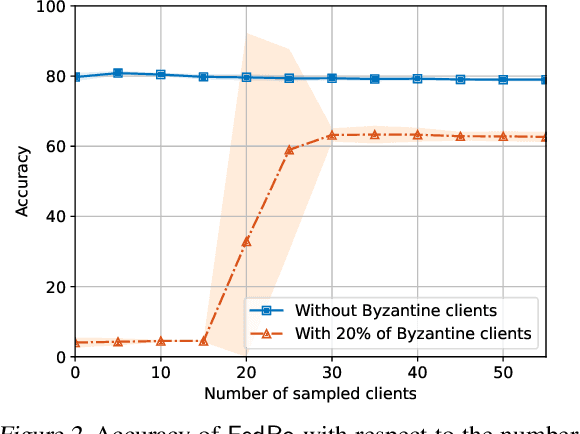
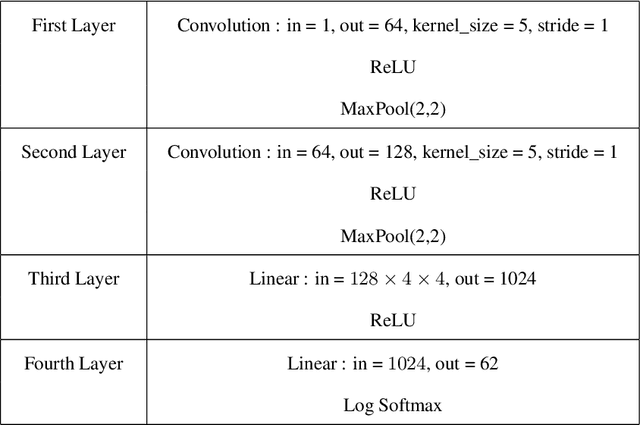
The possibility of adversarial (a.k.a., {\em Byzantine}) clients makes federated learning (FL) prone to arbitrary manipulation. The natural approach to robustify FL against adversarial clients is to replace the simple averaging operation at the server in the standard $\mathsf{FedAvg}$ algorithm by a \emph{robust averaging rule}. While a significant amount of work has been devoted to studying the convergence of federated {\em robust averaging} (which we denote by $\mathsf{FedRo}$), prior work has largely ignored the impact of {\em client subsampling} and {\em local steps}, two fundamental FL characteristics. While client subsampling increases the effective fraction of Byzantine clients, local steps increase the drift between the local updates computed by honest (i.e., non-Byzantine) clients. Consequently, a careless deployment of $\mathsf{FedRo}$ could yield poor performance. We validate this observation by presenting an in-depth analysis of $\mathsf{FedRo}$ tightly analyzing the impact of client subsampling and local steps. Specifically, we present a sufficient condition on client subsampling for nearly-optimal convergence of $\mathsf{FedRo}$ (for smooth non-convex loss). Also, we show that the rate of improvement in learning accuracy {\em diminishes} with respect to the number of clients subsampled, as soon as the sample size exceeds a threshold value. Interestingly, we also observe that under a careful choice of step-sizes, the learning error due to Byzantine clients decreases with the number of local steps. We validate our theory by experiments on the FEMNIST and CIFAR-$10$ image classification tasks.

Robust Distributed Learning: Tight Error Bounds and Breakdown Point under Data Heterogeneity

The theory underlying robust distributed learning algorithms, designed to resist adversarial machines, matches empirical observations when data is homogeneous. Under data heterogeneity however, which is the norm in practical scenarios, established lower bounds on the learning error are essentially vacuous and greatly mismatch empirical observations. This is because the heterogeneity model considered is too restrictive and does not cover basic learning tasks such as least-squares regression. We consider in this paper a more realistic heterogeneity model, namely (G,B)-gradient dissimilarity, and show that it covers a larger class of learning problems than existing theory. Notably, we show that the breakdown point under heterogeneity is lower than the classical fraction 1/2. We also prove a new lower bound on the learning error of any distributed learning algorithm. We derive a matching upper bound for a robust variant of distributed gradient descent, and empirically show that our analysis reduces the gap between theory and practice.

Distributed Learning with Curious and Adversarial Machines

The ubiquity of distributed machine learning (ML) in sensitive public domain applications calls for algorithms that protect data privacy, while being robust to faults and adversarial behaviors. Although privacy and robustness have been extensively studied independently in distributed ML, their synthesis remains poorly understood. We present the first tight analysis of the error incurred by any algorithm ensuring robustness against a fraction of adversarial machines, as well as differential privacy (DP) for honest machines' data against any other curious entity. Our analysis exhibits a fundamental trade-off between privacy, robustness, and utility. Surprisingly, we show that the cost of this trade-off is marginal compared to that of the classical privacy-utility trade-off. To prove our lower bound, we consider the case of mean estimation, subject to distributed DP and robustness constraints, and devise reductions to centralized estimation of one-way marginals. We prove our matching upper bound by presenting a new distributed ML algorithm using a high-dimensional robust aggregation rule. The latter amortizes the dependence on the dimension in the error (caused by adversarial workers and DP), while being agnostic to the statistical properties of the data.

Fixing by Mixing: A Recipe for Optimal Byzantine ML under Heterogeneity

Byzantine machine learning (ML) aims to ensure the resilience of distributed learning algorithms to misbehaving (or Byzantine) machines. Although this problem received significant attention, prior works often assume the data held by the machines to be homogeneous, which is seldom true in practical settings. Data heterogeneity makes Byzantine ML considerably more challenging, since a Byzantine machine can hardly be distinguished from a non-Byzantine outlier. A few solutions have been proposed to tackle this issue, but these provide suboptimal probabilistic guarantees and fare poorly in practice. This paper closes the theoretical gap, achieving optimality and inducing good empirical results. In fact, we show how to automatically adapt existing solutions for (homogeneous) Byzantine ML to the heterogeneous setting through a powerful mechanism, we call nearest neighbor mixing (NNM), which boosts any standard robust distributed gradient descent variant to yield optimal Byzantine resilience under heterogeneity. We obtain similar guarantees (in expectation) by plugging NNM in the distributed stochastic heavy ball method, a practical substitute to distributed gradient descent. We obtain empirical results that significantly outperform state-of-the-art Byzantine ML solutions.

Impact of Redundancy on Resilience in Distributed Optimization and Learning

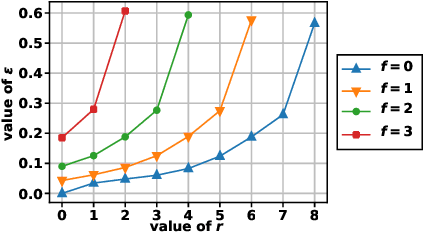
This report considers the problem of resilient distributed optimization and stochastic learning in a server-based architecture. The system comprises a server and multiple agents, where each agent has its own local cost function. The agents collaborate with the server to find a minimum of the aggregate of the local cost functions. In the context of stochastic learning, the local cost of an agent is the loss function computed over the data at that agent. In this report, we consider this problem in a system wherein some of the agents may be Byzantine faulty and some of the agents may be slow (also called stragglers). In this setting, we investigate the conditions under which it is possible to obtain an "approximate" solution to the above problem. In particular, we introduce the notion of $(f, r; \epsilon)$-resilience to characterize how well the true solution is approximated in the presence of up to $f$ Byzantine faulty agents, and up to $r$ slow agents (or stragglers) -- smaller $\epsilon$ represents a better approximation. We also introduce a measure named $(f, r; \epsilon)$-redundancy to characterize the redundancy in the cost functions of the agents. Greater redundancy allows for a better approximation when solving the problem of aggregate cost minimization. In this report, we constructively show (both theoretically and empirically) that $(f, r; \mathcal{O}(\epsilon))$-resilience can indeed be achieved in practice, given that the local cost functions are sufficiently redundant.

SoK: On the Impossible Security of Very Large Foundation Models

Large machine learning models, or so-called foundation models, aim to serve as base-models for application-oriented machine learning. Although these models showcase impressive performance, they have been empirically found to pose serious security and privacy issues. We may however wonder if this is a limitation of the current models, or if these issues stem from a fundamental intrinsic impossibility of the foundation model learning problem itself. This paper aims to systematize our knowledge supporting the latter. More precisely, we identify several key features of today's foundation model learning problem which, given the current understanding in adversarial machine learning, suggest incompatibility of high accuracy with both security and privacy. We begin by observing that high accuracy seems to require (1) very high-dimensional models and (2) huge amounts of data that can only be procured through user-generated datasets. Moreover, such data is fundamentally heterogeneous, as users generally have very specific (easily identifiable) data-generating habits. More importantly, users' data is filled with highly sensitive information, and maybe heavily polluted by fake users. We then survey lower bounds on accuracy in privacy-preserving and Byzantine-resilient heterogeneous learning that, we argue, constitute a compelling case against the possibility of designing a secure and privacy-preserving high-accuracy foundation model. We further stress that our analysis also applies to other high-stake machine learning applications, including content recommendation. We conclude by calling for measures to prioritize security and privacy, and to slow down the race for ever larger models.