Robust Distributed Learning: Tight Error Bounds and Breakdown Point under Data Heterogeneity

The theory underlying robust distributed learning algorithms, designed to resist adversarial machines, matches empirical observations when data is homogeneous. Under data heterogeneity however, which is the norm in practical scenarios, established lower bounds on the learning error are essentially vacuous and greatly mismatch empirical observations. This is because the heterogeneity model considered is too restrictive and does not cover basic learning tasks such as least-squares regression. We consider in this paper a more realistic heterogeneity model, namely (G,B)-gradient dissimilarity, and show that it covers a larger class of learning problems than existing theory. Notably, we show that the breakdown point under heterogeneity is lower than the classical fraction 1/2. We also prove a new lower bound on the learning error of any distributed learning algorithm. We derive a matching upper bound for a robust variant of distributed gradient descent, and empirically show that our analysis reduces the gap between theory and practice.

Differential Privacy and Byzantine Resilience in SGD: Do They Add Up?

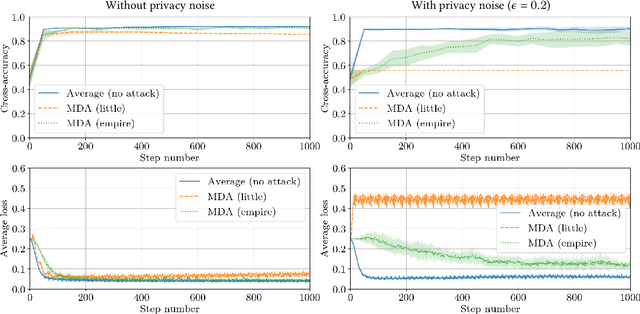
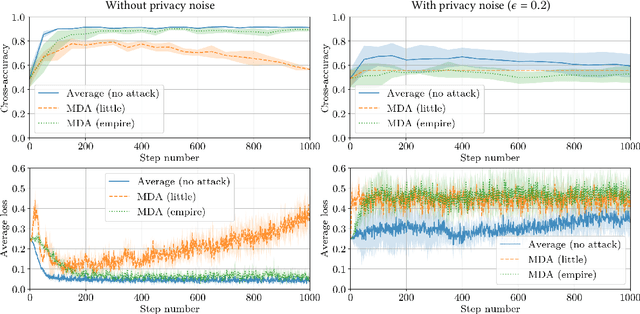
This paper addresses the problem of combining Byzantine resilience with privacy in machine learning (ML). Specifically, we study whether a distributed implementation of the renowned Stochastic Gradient Descent (SGD) learning algorithm is feasible with both differential privacy (DP) and $(\alpha,f)$-Byzantine resilience. To the best of our knowledge, this is the first work to tackle this problem from a theoretical point of view. A key finding of our analyses is that the classical approaches to these two (seemingly) orthogonal issues are incompatible. More precisely, we show that a direct composition of these techniques makes the guarantees of the resulting SGD algorithm depend unfavourably upon the number of parameters in the ML model, making the training of large models practically infeasible. We validate our theoretical results through numerical experiments on publicly-available datasets; showing that it is impractical to ensure DP and Byzantine resilience simultaneously.