Differential Privacy and Byzantine Resilience in SGD: Do They Add Up?

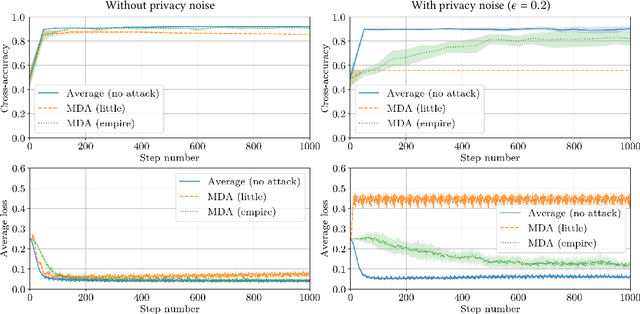
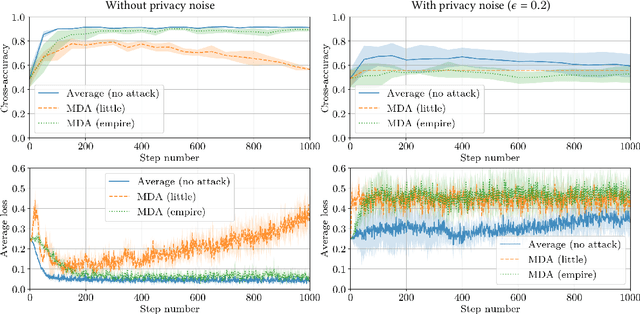
This paper addresses the problem of combining Byzantine resilience with privacy in machine learning (ML). Specifically, we study whether a distributed implementation of the renowned Stochastic Gradient Descent (SGD) learning algorithm is feasible with both differential privacy (DP) and $(\alpha,f)$-Byzantine resilience. To the best of our knowledge, this is the first work to tackle this problem from a theoretical point of view. A key finding of our analyses is that the classical approaches to these two (seemingly) orthogonal issues are incompatible. More precisely, we show that a direct composition of these techniques makes the guarantees of the resulting SGD algorithm depend unfavourably upon the number of parameters in the ML model, making the training of large models practically infeasible. We validate our theoretical results through numerical experiments on publicly-available datasets; showing that it is impractical to ensure DP and Byzantine resilience simultaneously.