Differential Privacy and Byzantine Resilience in SGD: Do They Add Up?

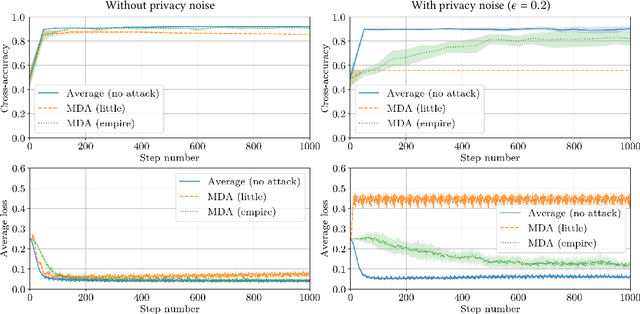
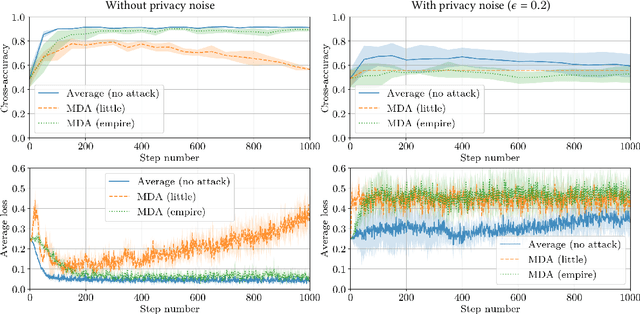
This paper addresses the problem of combining Byzantine resilience with privacy in machine learning (ML). Specifically, we study whether a distributed implementation of the renowned Stochastic Gradient Descent (SGD) learning algorithm is feasible with both differential privacy (DP) and $(\alpha,f)$-Byzantine resilience. To the best of our knowledge, this is the first work to tackle this problem from a theoretical point of view. A key finding of our analyses is that the classical approaches to these two (seemingly) orthogonal issues are incompatible. More precisely, we show that a direct composition of these techniques makes the guarantees of the resulting SGD algorithm depend unfavourably upon the number of parameters in the ML model, making the training of large models practically infeasible. We validate our theoretical results through numerical experiments on publicly-available datasets; showing that it is impractical to ensure DP and Byzantine resilience simultaneously.

Garfield: System Support for Byzantine Machine Learning

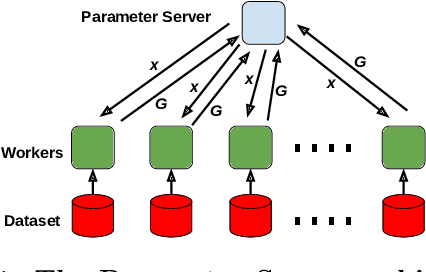
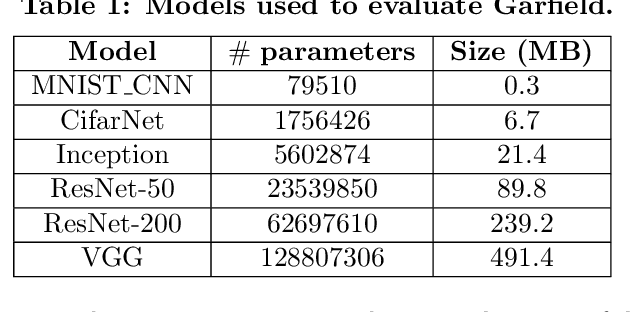
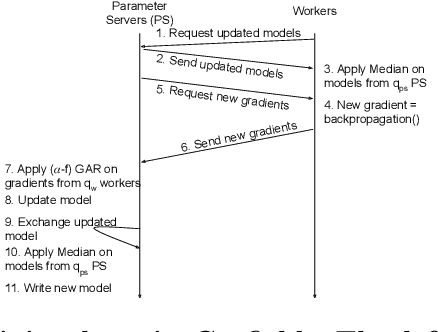
Byzantine Machine Learning (ML) systems are nowadays vulnerable for they require trusted machines and/or a synchronous network. We present Garfield, a system that provably achieves Byzantine resilience in ML applications without assuming any trusted component nor any bound on communication or computation delays. Garfield leverages ML specificities to make progress despite consensus being impossible in such an asynchronous, Byzantine environment. Following the classical server/worker architecture, Garfield replicates the parameter server while relying on the statistical properties of stochastic gradient descent to keep the models on the correct servers close to each other. On the other hand, Garfield uses statistically-robust gradient aggregation rules (GARs) to achieve resilience against Byzantine workers. We integrate Garfield with two widely-used ML frameworks, TensorFlow and PyTorch, while achieving transparency: applications developed with either framework do not need to change their interfaces to be made Byzantine resilient. Our implementation supports full-stack computations on both CPUs and GPUs. We report on our evaluation of Garfield with different (a) baselines, (b) ML models (e.g., ResNet-50 and VGG), and (c) hardware infrastructures (CPUs and GPUs). Our evaluation highlights several interesting facts about the cost of Byzantine resilience. In particular, (a) Byzantine resilience, unlike crash resilience, induces an accuracy loss, and (b) the throughput overhead comes much more from communication (70%) than from aggregation.

Collaborative Learning as an Agreement Problem

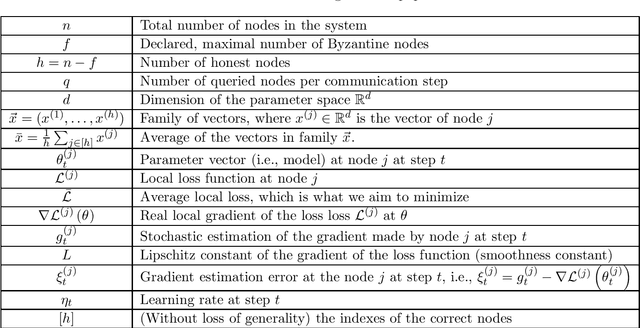
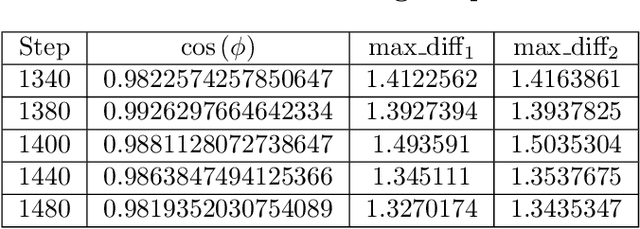
We address the problem of Byzantine collaborative learning: a set of $n$ nodes try to collectively learn from data, whose distributions may vary from one node to another. None of them is trusted and $f < n$ can behave arbitrarily. We show that collaborative learning is equivalent to a new form of agreement, which we call averaging agreement. In this problem, nodes start each with an initial vector and seek to approximately agree on a common vector, while guaranteeing that this common vector remains within a constant (also called averaging constant) of the maximum distance between the original vectors. Essentially, the smaller the averaging constant, the better the learning. We present three asynchronous solutions to averaging agreement, each interesting in its own right. The first, based on the minimum volume ellipsoid, achieves asymptotically the best-possible averaging constant but requires $ n \geq 6f+1$. The second, based on reliable broadcast, achieves optimal Byzantine resilience, i.e., $n \geq 3f+1$, but requires signatures and induces a large number of communication rounds. The third, based on coordinate-wise trimmed mean, is faster and achieves optimal Byzantine resilience, i.e., $n \geq 4f+1$, within standard form algorithms that do not use signatures.

Distributed Momentum for Byzantine-resilient Learning

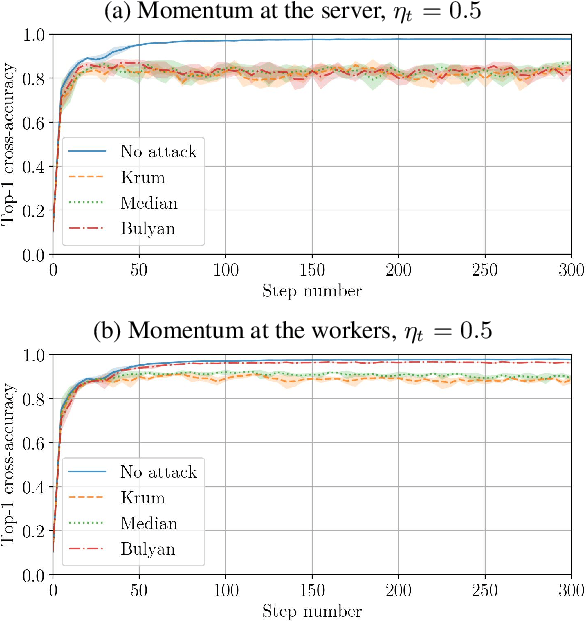
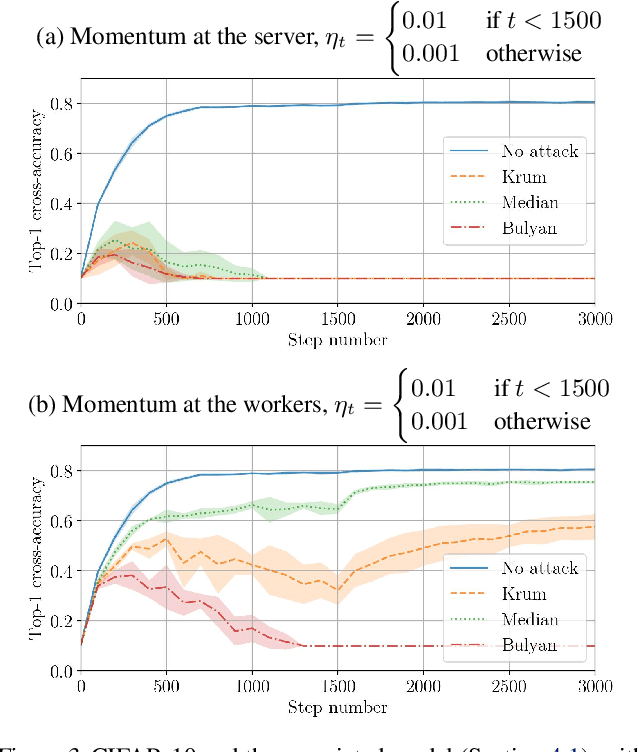
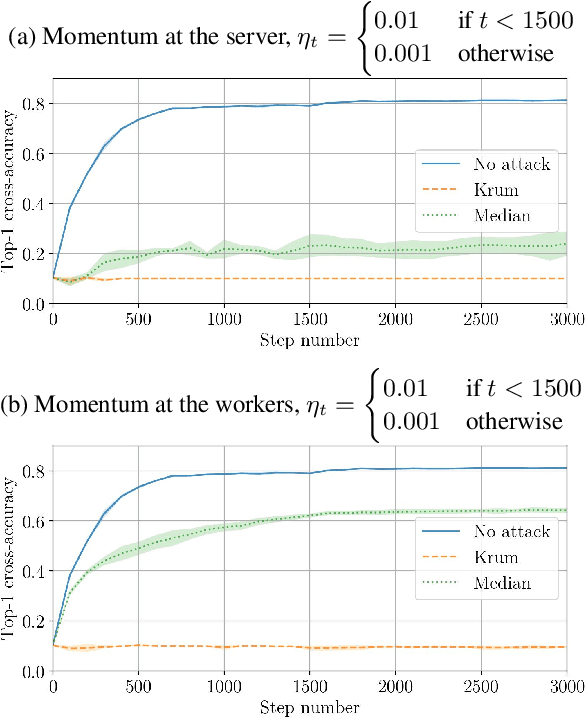
Momentum is a variant of gradient descent that has been proposed for its benefits on convergence. In a distributed setting, momentum can be implemented either at the server or the worker side. When the aggregation rule used by the server is linear, commutativity with addition makes both deployments equivalent. Robustness and privacy are however among motivations to abandon linear aggregation rules. In this work, we demonstrate the benefits on robustness of using momentum at the worker side. We first prove that computing momentum at the workers reduces the variance-norm ratio of the gradient estimation at the server, strengthening Byzantine resilient aggregation rules. We then provide an extensive experimental demonstration of the robustness effect of worker-side momentum on distributed SGD.

The Hidden Vulnerability of Distributed Learning in Byzantium

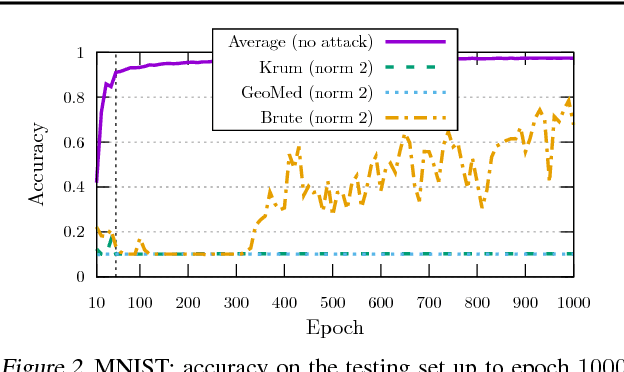
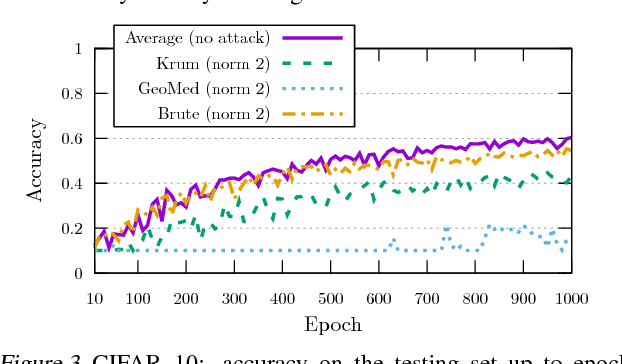
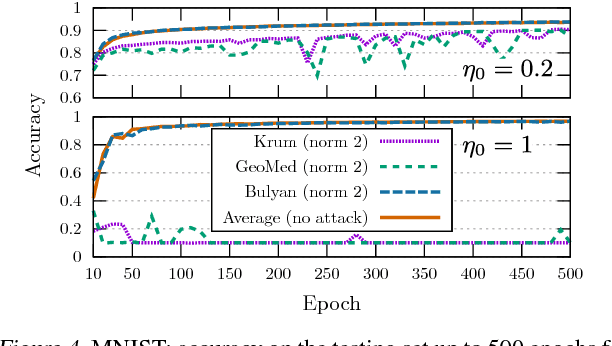
While machine learning is going through an era of celebrated success, concerns have been raised about the vulnerability of its backbone: stochastic gradient descent (SGD). Recent approaches have been proposed to ensure the robustness of distributed SGD against adversarial (Byzantine) workers sending poisoned gradients during the training phase. Some of these approaches have been proven Byzantine-resilient: they ensure the convergence of SGD despite the presence of a minority of adversarial workers. We show in this paper that convergence is not enough. In high dimension $d \gg 1$, an adver\-sary can build on the loss function's non-convexity to make SGD converge to ineffective models. More precisely, we bring to light that existing Byzantine-resilient schemes leave a margin of poisoning of $\Omega\left(f(d)\right)$, where $f(d)$ increases at least like $\sqrt{d~}$. Based on this leeway, we build a simple attack, and experimentally show its strong to utmost effectivity on CIFAR-10 and MNIST. We introduce Bulyan, and prove it significantly reduces the attackers leeway to a narrow $O( \frac{1}{\sqrt{d~}})$ bound. We empirically show that Bulyan does not suffer the fragility of existing aggregation rules and, at a reasonable cost in terms of required batch size, achieves convergence as if only non-Byzantine gradients had been used to update the model.