Arsany Guirguis
Accelerating Transfer Learning with Near-Data Computation on Cloud Object Stores
Oct 16, 2022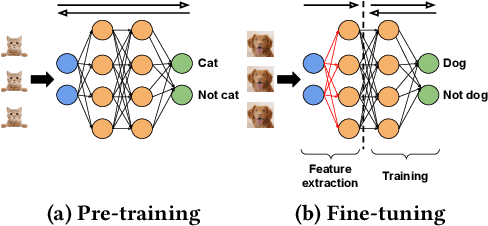
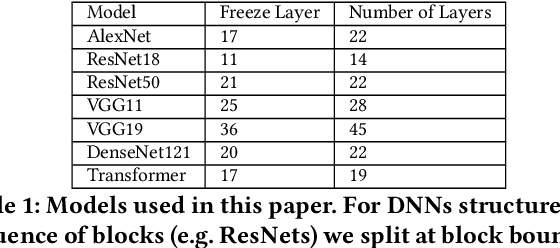
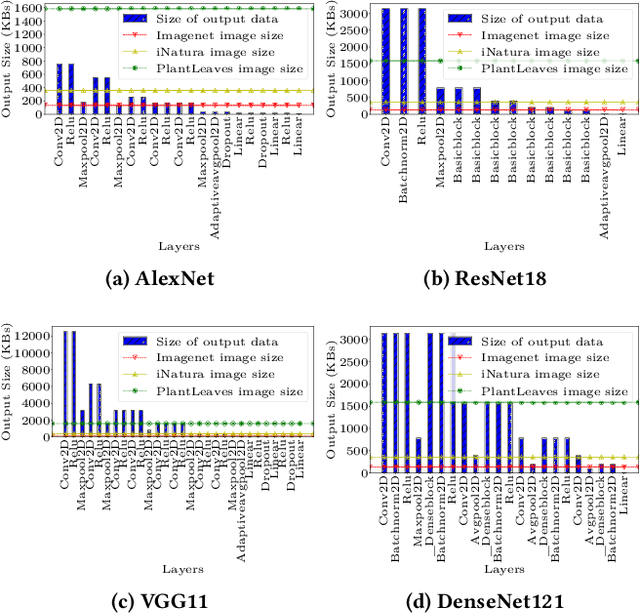
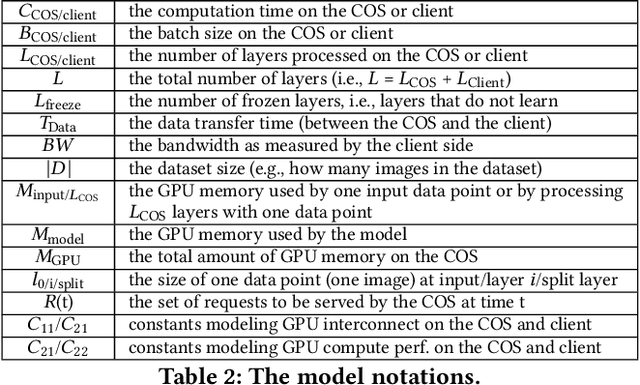
Abstract:Storage disaggregation is fundamental to today's cloud due to cost and scalability benefits. Unfortunately, this design must cope with an inherent network bottleneck between the storage and the compute tiers. The widely deployed mitigation strategy is to provide computational resources next to storage to push down a part of an application and thus reduce the amount of data transferred to the compute tier. Overall, users of disaggregated storage need to consider two main constraints: the network may remain a bottleneck, and the storage-side computational resources are limited. This paper identifies transfer learning (TL) as a natural fit for the disaggregated cloud. TL, famously described as the next driver of ML commercial success, is widely popular and has broad-range applications. We show how to leverage the unique structure of TL's fine-tuning phase (i.e., a combination of feature extraction and training) to flexibly address the aforementioned constraints and improve both user and operator-centric metrics. The key to improving user-perceived performance is to mitigate the network bottleneck by carefully splitting the TL deep neural network (DNN) such that feature extraction is, partially or entirely, executed next to storage. Crucially, such splitting enables decoupling the batch size of feature extraction from the training batch size, facilitating efficient storage-side batch size adaptation to increase concurrency in the storage tier while avoiding out-of-memory errors. Guided by these insights, we present HAPI, a processing system for TL that spans the compute and storage tiers while remaining transparent to the user. Our evaluation with several DNNs, such as ResNet, VGG, and Transformer, shows up to 11x improvement in application runtime and up to 8.3x reduction in the data transferred from the storage to the compute tier compared to running the computation in the compute tier.
Garfield: System Support for Byzantine Machine Learning
Oct 12, 2020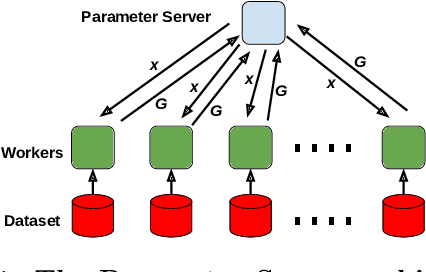
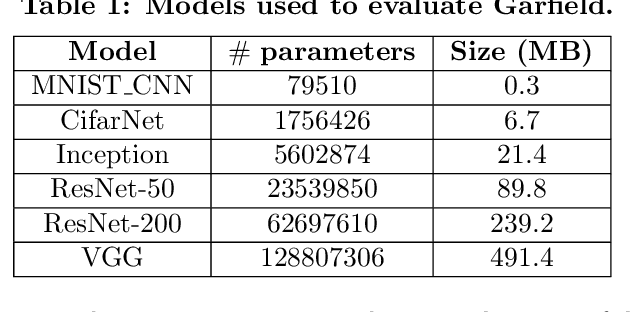
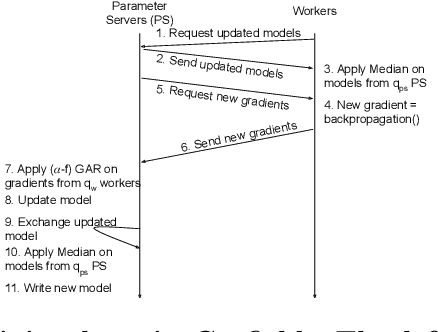
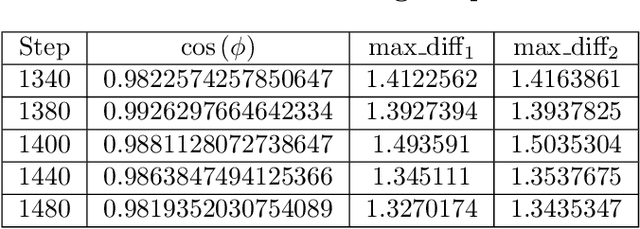
Abstract:Byzantine Machine Learning (ML) systems are nowadays vulnerable for they require trusted machines and/or a synchronous network. We present Garfield, a system that provably achieves Byzantine resilience in ML applications without assuming any trusted component nor any bound on communication or computation delays. Garfield leverages ML specificities to make progress despite consensus being impossible in such an asynchronous, Byzantine environment. Following the classical server/worker architecture, Garfield replicates the parameter server while relying on the statistical properties of stochastic gradient descent to keep the models on the correct servers close to each other. On the other hand, Garfield uses statistically-robust gradient aggregation rules (GARs) to achieve resilience against Byzantine workers. We integrate Garfield with two widely-used ML frameworks, TensorFlow and PyTorch, while achieving transparency: applications developed with either framework do not need to change their interfaces to be made Byzantine resilient. Our implementation supports full-stack computations on both CPUs and GPUs. We report on our evaluation of Garfield with different (a) baselines, (b) ML models (e.g., ResNet-50 and VGG), and (c) hardware infrastructures (CPUs and GPUs). Our evaluation highlights several interesting facts about the cost of Byzantine resilience. In particular, (a) Byzantine resilience, unlike crash resilience, induces an accuracy loss, and (b) the throughput overhead comes much more from communication (70%) than from aggregation.
Collaborative Learning as an Agreement Problem
Aug 04, 2020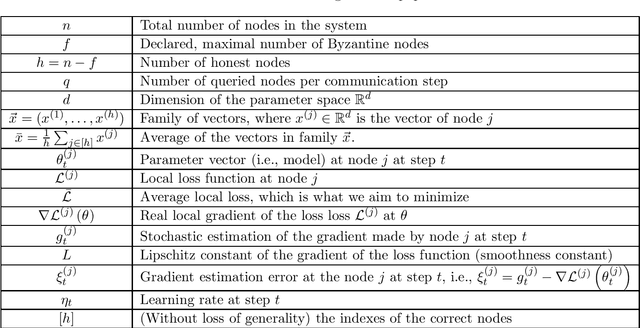
Abstract:We address the problem of Byzantine collaborative learning: a set of $n$ nodes try to collectively learn from data, whose distributions may vary from one node to another. None of them is trusted and $f < n$ can behave arbitrarily. We show that collaborative learning is equivalent to a new form of agreement, which we call averaging agreement. In this problem, nodes start each with an initial vector and seek to approximately agree on a common vector, while guaranteeing that this common vector remains within a constant (also called averaging constant) of the maximum distance between the original vectors. Essentially, the smaller the averaging constant, the better the learning. We present three asynchronous solutions to averaging agreement, each interesting in its own right. The first, based on the minimum volume ellipsoid, achieves asymptotically the best-possible averaging constant but requires $ n \geq 6f+1$. The second, based on reliable broadcast, achieves optimal Byzantine resilience, i.e., $n \geq 3f+1$, but requires signatures and induces a large number of communication rounds. The third, based on coordinate-wise trimmed mean, is faster and achieves optimal Byzantine resilience, i.e., $n \geq 4f+1$, within standard form algorithms that do not use signatures.
Fast Machine Learning with Byzantine Workers and Servers
Nov 18, 2019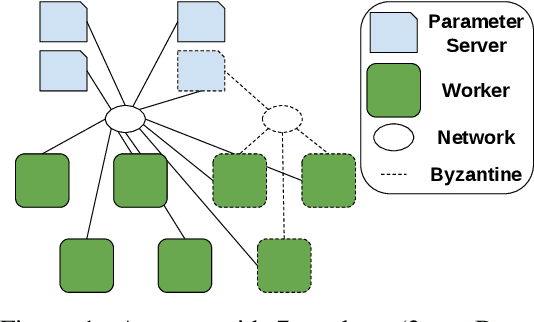
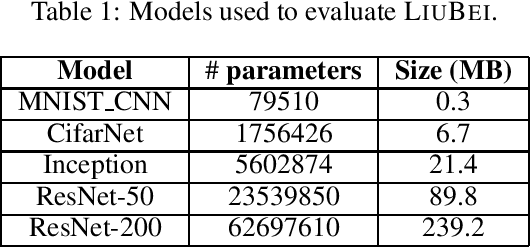
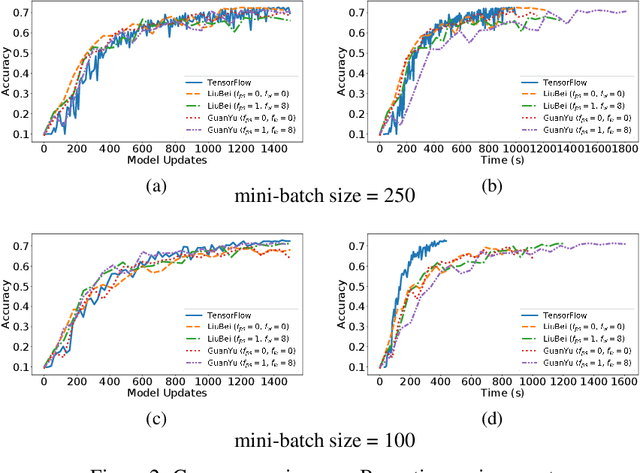
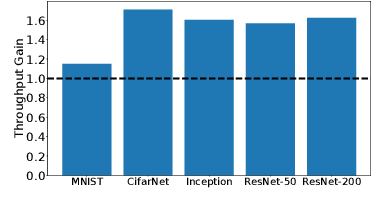
Abstract:Machine Learning (ML) solutions are nowadays distributed and are prone to various types of component failures, which can be encompassed in so-called Byzantine behavior. This paper introduces LiuBei, a Byzantine-resilient ML algorithm that does not trust any individual component in the network (neither workers nor servers), nor does it induce additional communication rounds (on average), compared to standard non-Byzantine resilient algorithms. LiuBei builds upon gradient aggregation rules (GARs) to tolerate a minority of Byzantine workers. Besides, LiuBei replicates the parameter server on multiple machines instead of trusting it. We introduce a novel filtering mechanism that enables workers to filter out replies from Byzantine server replicas without requiring communication with all servers. Such a filtering mechanism is based on network synchrony, Lipschitz continuity of the loss function, and the GAR used to aggregate workers' gradients. We also introduce a protocol, scatter/gather, to bound drifts between models on correct servers with a small number of communication messages. We theoretically prove that LiuBei achieves Byzantine resilience to both servers and workers and guarantees convergence. We build LiuBei using TensorFlow, and we show that LiuBei tolerates Byzantine behavior with an accuracy loss of around 5% and around 24% convergence overhead compared to vanilla TensorFlow. We moreover show that the throughput gain of LiuBei compared to another state-of-the-art Byzantine-resilient ML algorithm (that assumes network asynchrony) is 70%.
SGD: Decentralized Byzantine Resilience
May 05, 2019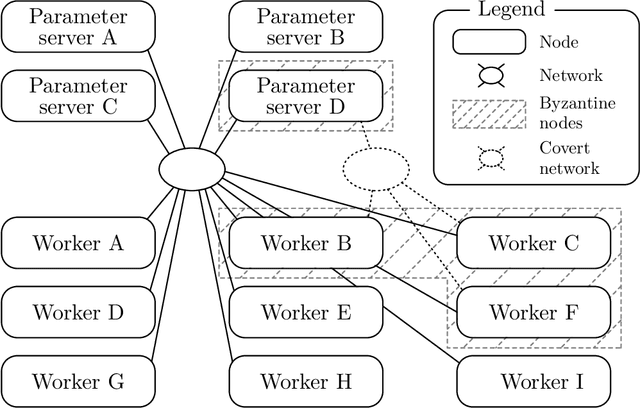

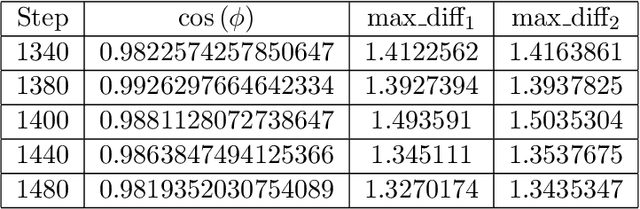
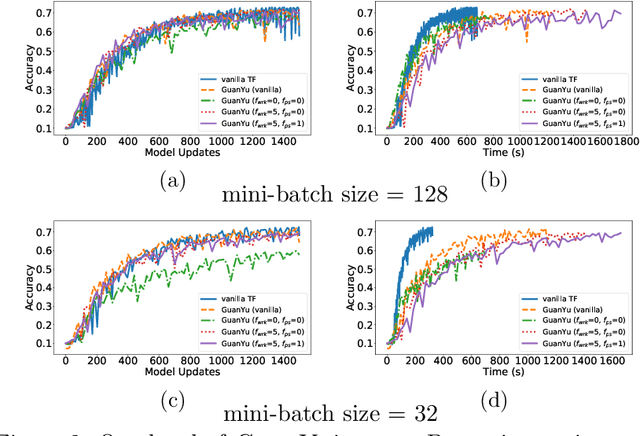
Abstract:The size of the datasets available today leads to distribute Machine Learning (ML) tasks. An SGD--based optimization is for instance typically carried out by two categories of participants: parameter servers and workers. Some of these nodes can sometimes behave arbitrarily (called \emph{Byzantine} and caused by corrupt/bogus data/machines), impacting the accuracy of the entire learning activity. Several approaches recently studied how to tolerate Byzantine workers, while assuming honest and trusted parameter servers. In order to achieve total ML robustness, we introduce GuanYu, the first algorithm (to the best of our knowledge) to handle Byzantine parameter servers as well as Byzantine workers. We prove that GuanYu ensures convergence against $\frac{1}{3}$ Byzantine parameter servers and $\frac{1}{3}$ Byzantine workers, which is optimal in asynchronous networks (GuanYu does also tolerate unbounded communication delays, i.e.\ asynchrony). To prove the Byzantine resilience of GuanYu, we use a contraction argument, leveraging geometric properties of the median in high dimensional spaces to prevent (with probability 1) any drift on the models within each of the non-Byzantine servers. % To convey its practicality, we implemented GuanYu using the low-level TensorFlow APIs and deployed it in a distributed setup using the CIFAR-10 dataset. The overhead of tolerating Byzantine participants, compared to a vanilla TensorFlow deployment that is vulnerable to a single Byzantine participant, is around 30\% in terms of throughput (model updates per second) - while maintaining the same convergence rate (model updates required to reach some accuracy).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge