Incentivized Learning in Principal-Agent Bandit Games

This work considers a repeated principal-agent bandit game, where the principal can only interact with her environment through the agent. The principal and the agent have misaligned objectives and the choice of action is only left to the agent. However, the principal can influence the agent's decisions by offering incentives which add up to his rewards. The principal aims to iteratively learn an incentive policy to maximize her own total utility. This framework extends usual bandit problems and is motivated by several practical applications, such as healthcare or ecological taxation, where traditionally used mechanism design theories often overlook the learning aspect of the problem. We present nearly optimal (with respect to a horizon $T$) learning algorithms for the principal's regret in both multi-armed and linear contextual settings. Finally, we support our theoretical guarantees through numerical experiments.

Host-Pathongen Co-evolution Inspired Algorithm Enables Robust GAN Training

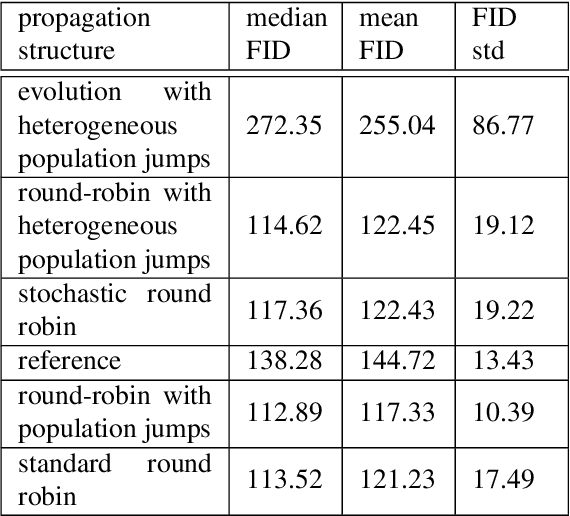
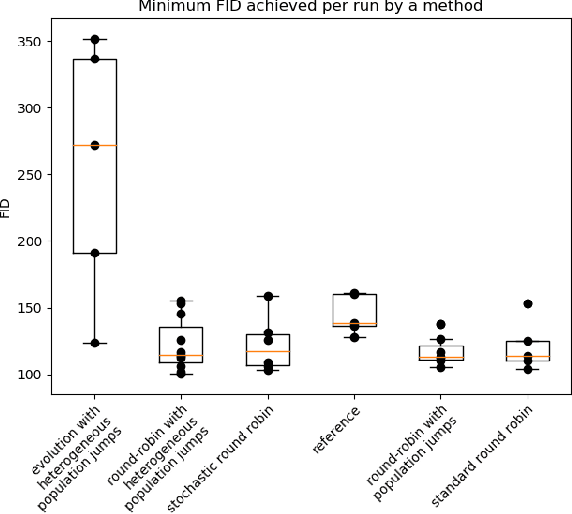
Generative adversarial networks (GANs) are pairs of artificial neural networks that are trained one against each other. The outputs from a generator are mixed with the real-world inputs to the discriminator and both networks are trained until an equilibrium is reached, where the discriminator cannot distinguish generated inputs from real ones. Since their introduction, GANs have allowed for the generation of impressive imitations of real-life films, images and texts, whose fakeness is barely noticeable to humans. Despite their impressive performance, training GANs remains to this day more of an art than a reliable procedure, in a large part due to training process stability. Generators are susceptible to mode dropping and convergence to random patterns, which have to be mitigated by computationally expensive multiple restarts. Curiously, GANs bear an uncanny similarity to a co-evolution of a pathogen and its host's immune system in biology. In a biological context, the majority of potential pathogens indeed never make it and are kept at bay by the hots' immune system. Yet some are efficient enough to present a risk of a serious condition and recurrent infections. Here, we explore that similarity to propose a more robust algorithm for GANs training. We empirically show the increased stability and a better ability to generate high-quality images while using less computational power.

Fast Machine Learning with Byzantine Workers and Servers

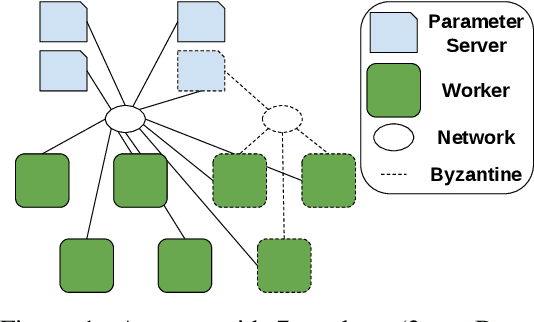
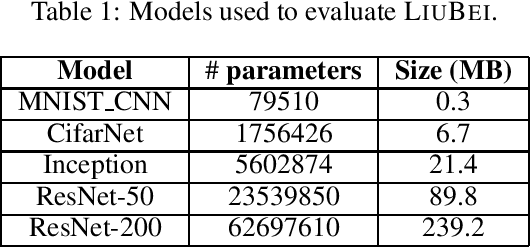
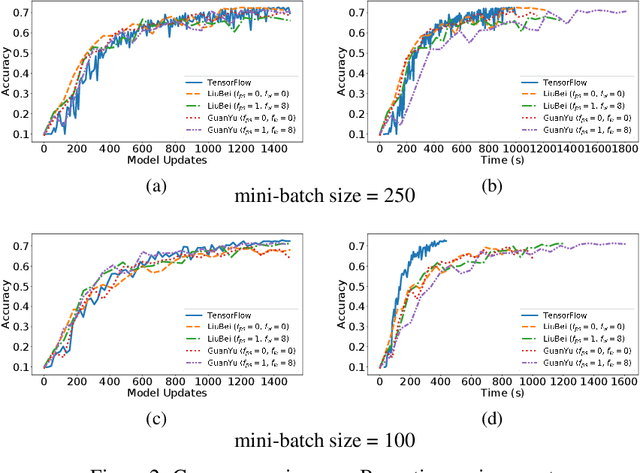
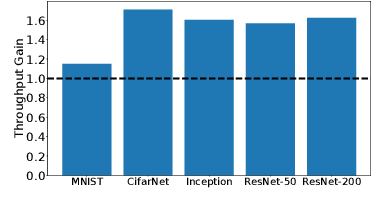
Machine Learning (ML) solutions are nowadays distributed and are prone to various types of component failures, which can be encompassed in so-called Byzantine behavior. This paper introduces LiuBei, a Byzantine-resilient ML algorithm that does not trust any individual component in the network (neither workers nor servers), nor does it induce additional communication rounds (on average), compared to standard non-Byzantine resilient algorithms. LiuBei builds upon gradient aggregation rules (GARs) to tolerate a minority of Byzantine workers. Besides, LiuBei replicates the parameter server on multiple machines instead of trusting it. We introduce a novel filtering mechanism that enables workers to filter out replies from Byzantine server replicas without requiring communication with all servers. Such a filtering mechanism is based on network synchrony, Lipschitz continuity of the loss function, and the GAR used to aggregate workers' gradients. We also introduce a protocol, scatter/gather, to bound drifts between models on correct servers with a small number of communication messages. We theoretically prove that LiuBei achieves Byzantine resilience to both servers and workers and guarantees convergence. We build LiuBei using TensorFlow, and we show that LiuBei tolerates Byzantine behavior with an accuracy loss of around 5% and around 24% convergence overhead compared to vanilla TensorFlow. We moreover show that the throughput gain of LiuBei compared to another state-of-the-art Byzantine-resilient ML algorithm (that assumes network asynchrony) is 70%.

Fatal Brain Damage

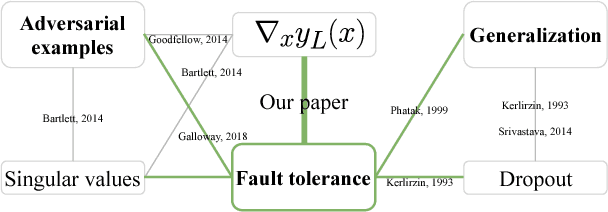
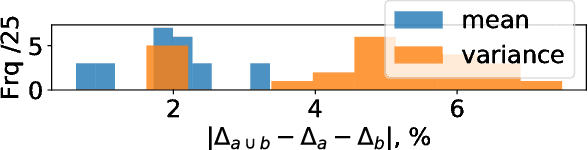
The loss of a few neurons in a brain often does not result in a visible loss of function. We propose to advance the understanding of neural networks through their remarkable ability to sustain individual neuron failures, i.e. their fault tolerance. Before the last AI winter, fault tolerance in NNs was a popular topic as NNs were expected to be implemented in neuromorphic hardware, which for a while did not happen. Moreover, since the number of possible crash subsets grows exponentially with the network size, additional assumptions are required to practically study this phenomenon for modern architectures. We prove a series of bounds on error propagation using justified assumptions, applicable to deep networks, show their location on the complexity versus tightness trade-off scale and test them empirically. We demonstrate how fault tolerance is connected to generalization and show that the data jacobian of a network determines its fault tolerance properties. We investigate this quantity and show how it is interlinked with other mathematical properties of the network such as Lipschitzness, singular values, weight matrices norms, and the loss gradients. Known results give a connection between the data jacobian and robustness to adversarial examples, providing another piece of the puzzle. Combining that with our results, we call for a unifying research endeavor encompassing fault tolerance, generalization capacity, and robustness to adversarial inputs together as we demonstrate a strong connection between these areas. Moreover, we argue that fault tolerance is an important overlooked AI safety problem since neuromorphic hardware is becoming popular again.

The Hidden Vulnerability of Distributed Learning in Byzantium

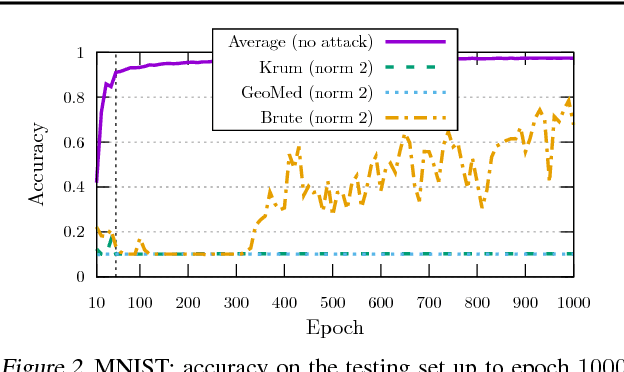
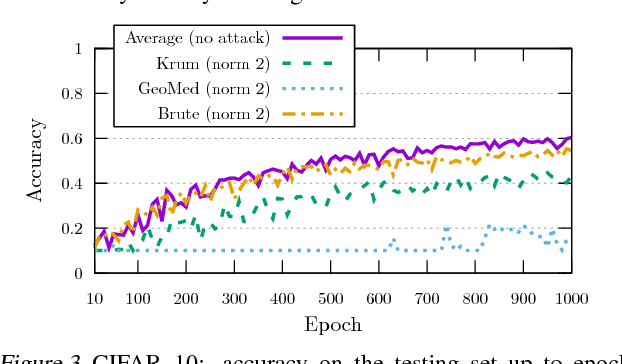
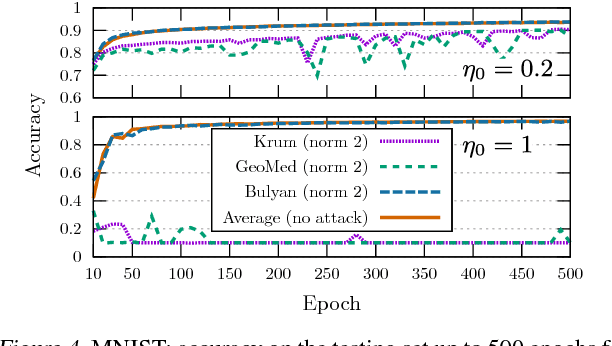
While machine learning is going through an era of celebrated success, concerns have been raised about the vulnerability of its backbone: stochastic gradient descent (SGD). Recent approaches have been proposed to ensure the robustness of distributed SGD against adversarial (Byzantine) workers sending poisoned gradients during the training phase. Some of these approaches have been proven Byzantine-resilient: they ensure the convergence of SGD despite the presence of a minority of adversarial workers. We show in this paper that convergence is not enough. In high dimension $d \gg 1$, an adver\-sary can build on the loss function's non-convexity to make SGD converge to ineffective models. More precisely, we bring to light that existing Byzantine-resilient schemes leave a margin of poisoning of $\Omega\left(f(d)\right)$, where $f(d)$ increases at least like $\sqrt{d~}$. Based on this leeway, we build a simple attack, and experimentally show its strong to utmost effectivity on CIFAR-10 and MNIST. We introduce Bulyan, and prove it significantly reduces the attackers leeway to a narrow $O( \frac{1}{\sqrt{d~}})$ bound. We empirically show that Bulyan does not suffer the fragility of existing aggregation rules and, at a reasonable cost in terms of required batch size, achieves convergence as if only non-Byzantine gradients had been used to update the model.

Asynchronous Byzantine Machine Learning (the case of SGD)

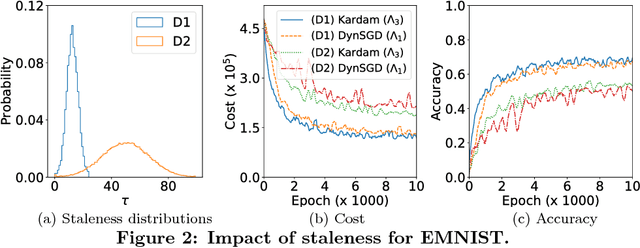
Asynchronous distributed machine learning solutions have proven very effective so far, but always assuming perfectly functioning workers. In practice, some of the workers can however exhibit Byzantine behavior, caused by hardware failures, software bugs, corrupt data, or even malicious attacks. We introduce \emph{Kardam}, the first distributed asynchronous stochastic gradient descent (SGD) algorithm that copes with Byzantine workers. Kardam consists of two complementary components: a filtering and a dampening component. The first is scalar-based and ensures resilience against $\frac{1}{3}$ Byzantine workers. Essentially, this filter leverages the Lipschitzness of cost functions and acts as a self-stabilizer against Byzantine workers that would attempt to corrupt the progress of SGD. The dampening component bounds the convergence rate by adjusting to stale information through a generic gradient weighting scheme. We prove that Kardam guarantees almost sure convergence in the presence of asynchrony and Byzantine behavior, and we derive its convergence rate. We evaluate Kardam on the CIFAR-100 and EMNIST datasets and measure its overhead with respect to non Byzantine-resilient solutions. We empirically show that Kardam does not introduce additional noise to the learning procedure but does induce a slowdown (the cost of Byzantine resilience) that we both theoretically and empirically show to be less than $f/n$, where $f$ is the number of Byzantine failures tolerated and $n$ the total number of workers. Interestingly, we also empirically observe that the dampening component is interesting in its own right for it enables to build an SGD algorithm that outperforms alternative staleness-aware asynchronous competitors in environments with honest workers.

Removing Algorithmic Discrimination (With Minimal Individual Error)

We address the problem of correcting group discriminations within a score function, while minimizing the individual error. Each group is described by a probability density function on the set of profiles. We first solve the problem analytically in the case of two populations, with a uniform bonus-malus on the zones where each population is a majority. We then address the general case of n populations, where the entanglement of populations does not allow a similar analytical solution. We show that an approximate solution with an arbitrarily high level of precision can be computed with linear programming. Finally, we address the inverse problem where the error should not go beyond a certain value and we seek to minimize the discrimination.

Virtuously Safe Reinforcement Learning

We show that when a third party, the adversary, steps into the two-party setting (agent and operator) of safely interruptible reinforcement learning, a trade-off has to be made between the probability of following the optimal policy in the limit, and the probability of escaping a dangerous situation created by the adversary. So far, the work on safely interruptible agents has assumed a perfect perception of the agent about its environment (no adversary), and therefore implicitly set the second probability to zero, by explicitly seeking a value of one for the first probability. We show that (1) agents can be made both interruptible and adversary-resilient, and (2) the interruptibility can be made safe in the sense that the agent itself will not seek to avoid it. We also solve the problem that arises when the agent does not go completely greedy, i.e. issues with safe exploration in the limit. Resilience to perturbed perception, safe exploration in the limit, and safe interruptibility are the three pillars of what we call \emph{virtuously safe reinforcement learning}.

Learning to Gather without Communication

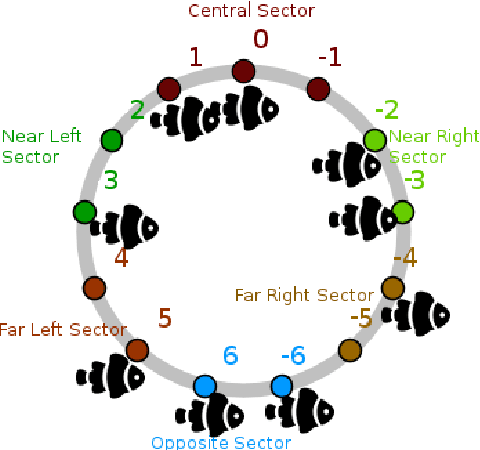
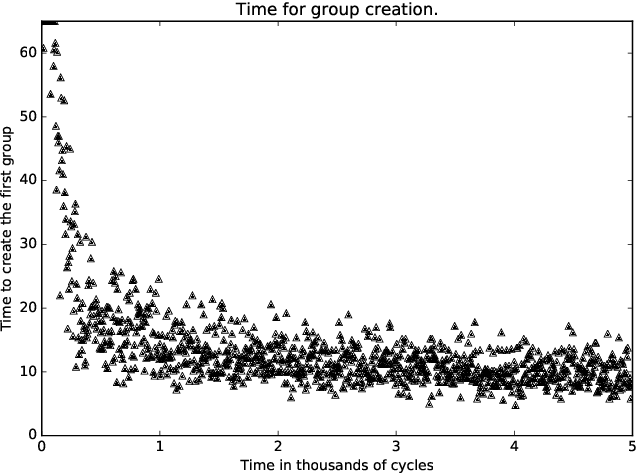
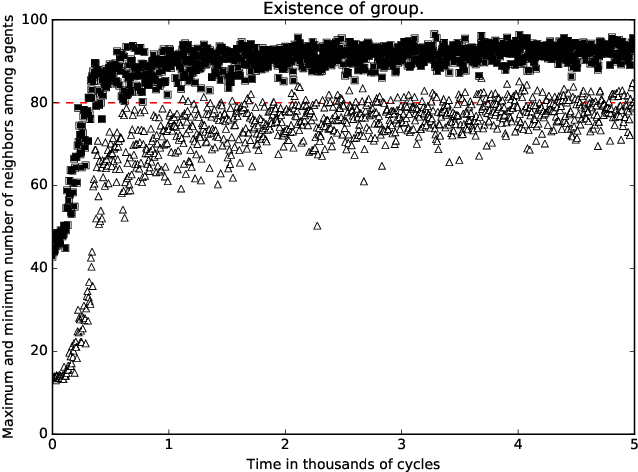
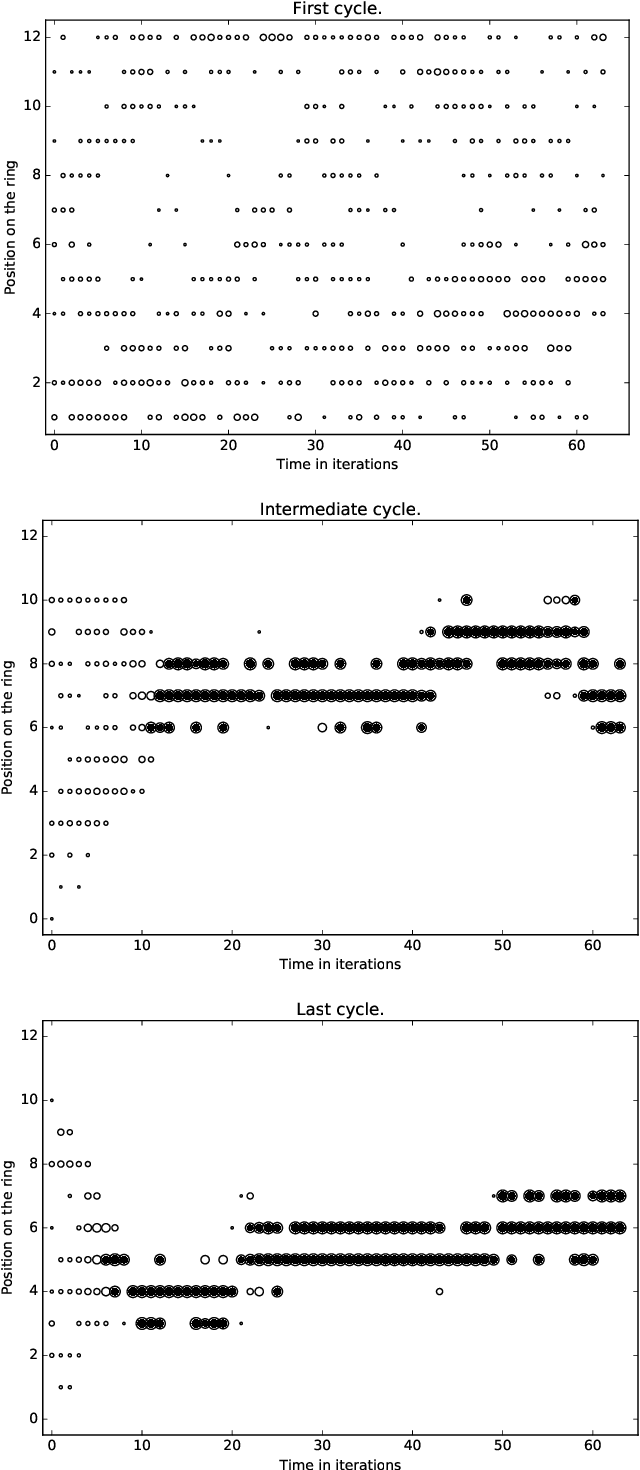
A standard belief on emerging collective behavior is that it emerges from simple individual rules. Most of the mathematical research on such collective behavior starts from imperative individual rules, like always go to the center. But how could an (optimal) individual rule emerge during a short period within the group lifetime, especially if communication is not available. We argue that such rules can actually emerge in a group in a short span of time via collective (multi-agent) reinforcement learning, i.e learning via rewards and punishments. We consider the gathering problem: several agents (social animals, swarming robots...) must gather around a same position, which is not determined in advance. They must do so without communication on their planned decision, just by looking at the position of other agents. We present the first experimental evidence that a gathering behavior can be learned without communication in a partially observable environment. The learned behavior has the same properties as a self-stabilizing distributed algorithm, as processes can gather from any initial state (and thus tolerate any transient failure). Besides, we show that it is possible to tolerate the brutal loss of up to 90\% of agents without significant impact on the behavior.

On The Robustness of a Neural Network

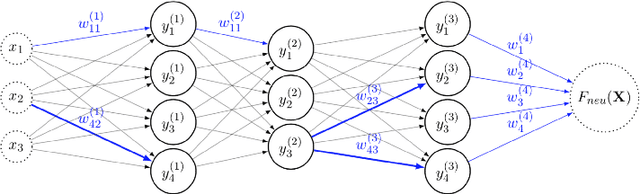
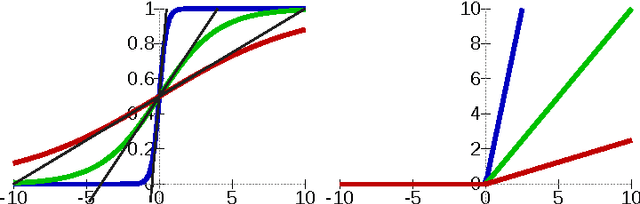
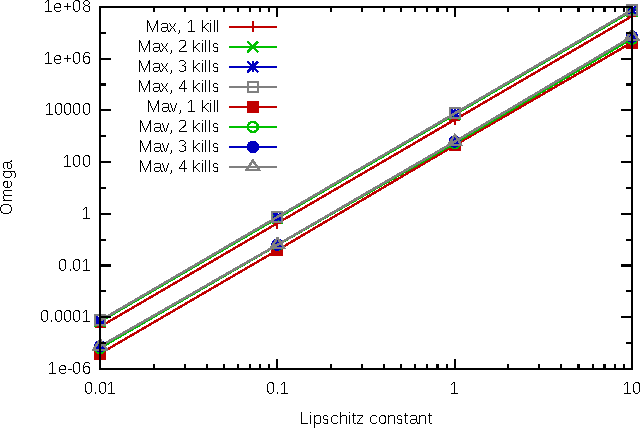
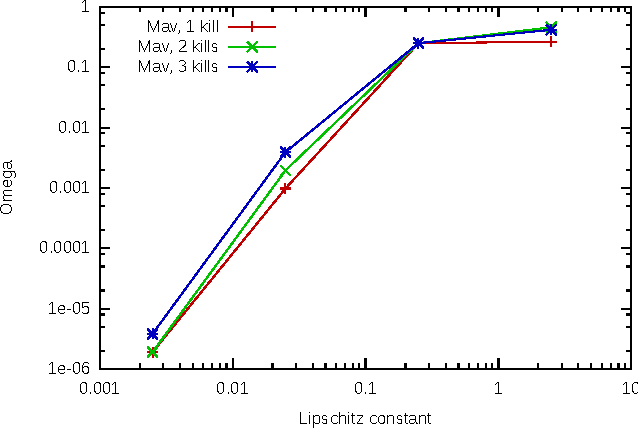
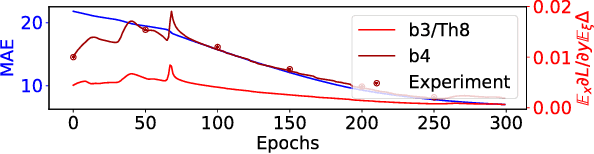
With the development of neural networks based machine learning and their usage in mission critical applications, voices are rising against the \textit{black box} aspect of neural networks as it becomes crucial to understand their limits and capabilities. With the rise of neuromorphic hardware, it is even more critical to understand how a neural network, as a distributed system, tolerates the failures of its computing nodes, neurons, and its communication channels, synapses. Experimentally assessing the robustness of neural networks involves the quixotic venture of testing all the possible failures, on all the possible inputs, which ultimately hits a combinatorial explosion for the first, and the impossibility to gather all the possible inputs for the second. In this paper, we prove an upper bound on the expected error of the output when a subset of neurons crashes. This bound involves dependencies on the network parameters that can be seen as being too pessimistic in the average case. It involves a polynomial dependency on the Lipschitz coefficient of the neurons activation function, and an exponential dependency on the depth of the layer where a failure occurs. We back up our theoretical results with experiments illustrating the extent to which our prediction matches the dependencies between the network parameters and robustness. Our results show that the robustness of neural networks to the average crash can be estimated without the need to neither test the network on all failure configurations, nor access the training set used to train the network, both of which are practically impossible requirements.