Fatal Brain Damage

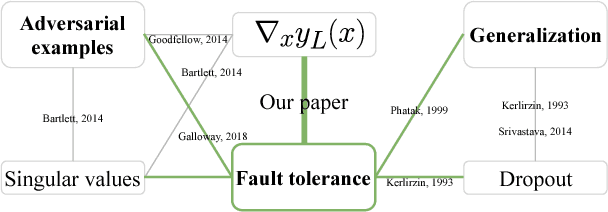
The loss of a few neurons in a brain often does not result in a visible loss of function. We propose to advance the understanding of neural networks through their remarkable ability to sustain individual neuron failures, i.e. their fault tolerance. Before the last AI winter, fault tolerance in NNs was a popular topic as NNs were expected to be implemented in neuromorphic hardware, which for a while did not happen. Moreover, since the number of possible crash subsets grows exponentially with the network size, additional assumptions are required to practically study this phenomenon for modern architectures. We prove a series of bounds on error propagation using justified assumptions, applicable to deep networks, show their location on the complexity versus tightness trade-off scale and test them empirically. We demonstrate how fault tolerance is connected to generalization and show that the data jacobian of a network determines its fault tolerance properties. We investigate this quantity and show how it is interlinked with other mathematical properties of the network such as Lipschitzness, singular values, weight matrices norms, and the loss gradients. Known results give a connection between the data jacobian and robustness to adversarial examples, providing another piece of the puzzle. Combining that with our results, we call for a unifying research endeavor encompassing fault tolerance, generalization capacity, and robustness to adversarial inputs together as we demonstrate a strong connection between these areas. Moreover, we argue that fault tolerance is an important overlooked AI safety problem since neuromorphic hardware is becoming popular again.