Fast Machine Learning with Byzantine Workers and Servers
Paper and Code
Nov 18, 2019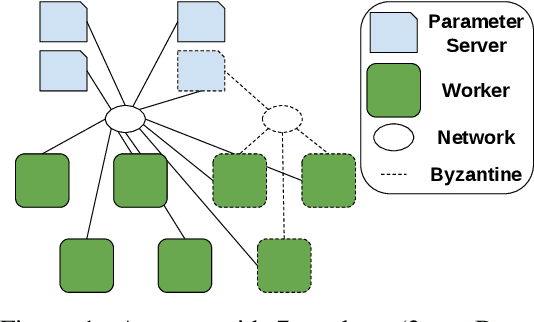
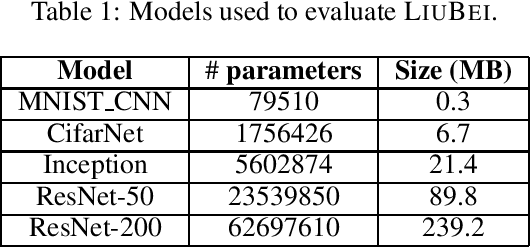
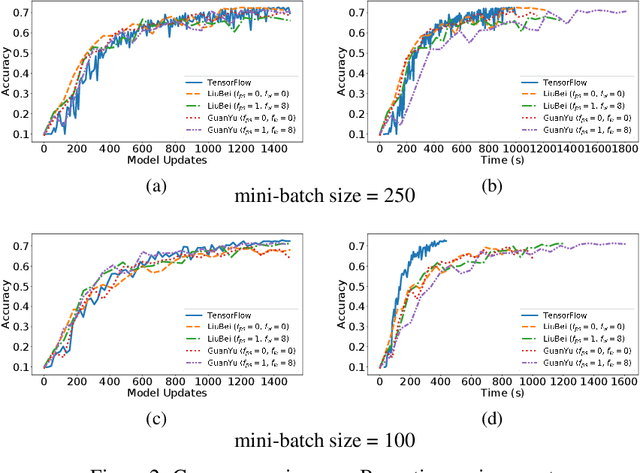
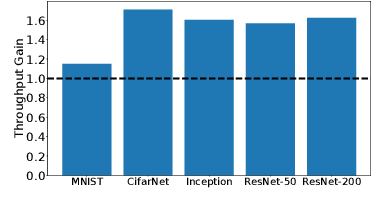
Machine Learning (ML) solutions are nowadays distributed and are prone to various types of component failures, which can be encompassed in so-called Byzantine behavior. This paper introduces LiuBei, a Byzantine-resilient ML algorithm that does not trust any individual component in the network (neither workers nor servers), nor does it induce additional communication rounds (on average), compared to standard non-Byzantine resilient algorithms. LiuBei builds upon gradient aggregation rules (GARs) to tolerate a minority of Byzantine workers. Besides, LiuBei replicates the parameter server on multiple machines instead of trusting it. We introduce a novel filtering mechanism that enables workers to filter out replies from Byzantine server replicas without requiring communication with all servers. Such a filtering mechanism is based on network synchrony, Lipschitz continuity of the loss function, and the GAR used to aggregate workers' gradients. We also introduce a protocol, scatter/gather, to bound drifts between models on correct servers with a small number of communication messages. We theoretically prove that LiuBei achieves Byzantine resilience to both servers and workers and guarantees convergence. We build LiuBei using TensorFlow, and we show that LiuBei tolerates Byzantine behavior with an accuracy loss of around 5% and around 24% convergence overhead compared to vanilla TensorFlow. We moreover show that the throughput gain of LiuBei compared to another state-of-the-art Byzantine-resilient ML algorithm (that assumes network asynchrony) is 70%.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge