Combining Differential Privacy and Byzantine Resilience in Distributed SGD

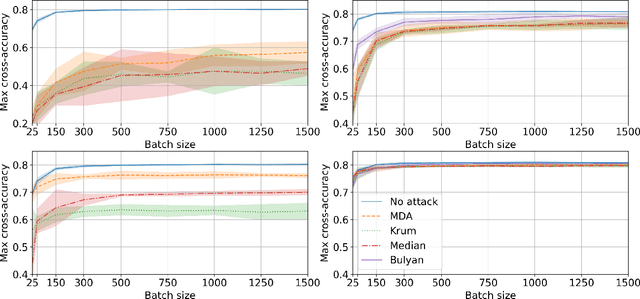
Privacy and Byzantine resilience (BR) are two crucial requirements of modern-day distributed machine learning. The two concepts have been extensively studied individually but the question of how to combine them effectively remains unanswered. This paper contributes to addressing this question by studying the extent to which the distributed SGD algorithm, in the standard parameter-server architecture, can learn an accurate model despite (a) a fraction of the workers being malicious (Byzantine), and (b) the other fraction, whilst being honest, providing noisy information to the server to ensure differential privacy (DP). We first observe that the integration of standard practices in DP and BR is not straightforward. In fact, we show that many existing results on the convergence of distributed SGD under Byzantine faults, especially those relying on $(\alpha,f)$-Byzantine resilience, are rendered invalid when honest workers enforce DP. To circumvent this shortcoming, we revisit the theory of $(\alpha,f)$-BR to obtain an approximate convergence guarantee. Our analysis provides key insights on how to improve this guarantee through hyperparameter optimization. Essentially, our theoretical and empirical results show that (1) an imprudent combination of standard approaches to DP and BR might be fruitless, but (2) by carefully re-tuning the learning algorithm, we can obtain reasonable learning accuracy while simultaneously guaranteeing DP and BR.

SGD: Decentralized Byzantine Resilience

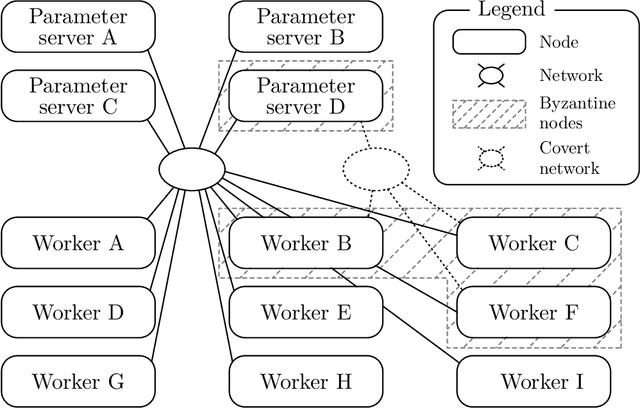
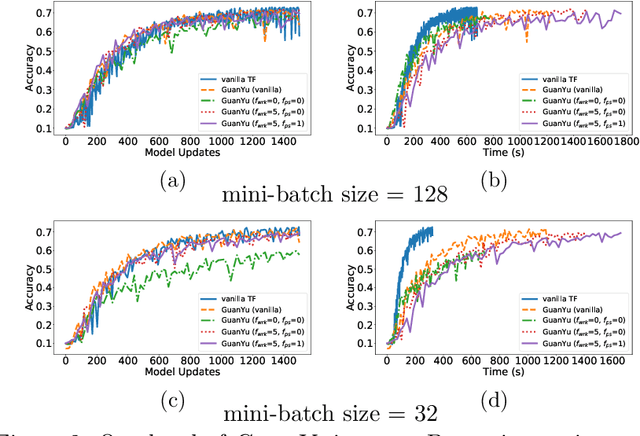
The size of the datasets available today leads to distribute Machine Learning (ML) tasks. An SGD--based optimization is for instance typically carried out by two categories of participants: parameter servers and workers. Some of these nodes can sometimes behave arbitrarily (called \emph{Byzantine} and caused by corrupt/bogus data/machines), impacting the accuracy of the entire learning activity. Several approaches recently studied how to tolerate Byzantine workers, while assuming honest and trusted parameter servers. In order to achieve total ML robustness, we introduce GuanYu, the first algorithm (to the best of our knowledge) to handle Byzantine parameter servers as well as Byzantine workers. We prove that GuanYu ensures convergence against $\frac{1}{3}$ Byzantine parameter servers and $\frac{1}{3}$ Byzantine workers, which is optimal in asynchronous networks (GuanYu does also tolerate unbounded communication delays, i.e.\ asynchrony). To prove the Byzantine resilience of GuanYu, we use a contraction argument, leveraging geometric properties of the median in high dimensional spaces to prevent (with probability 1) any drift on the models within each of the non-Byzantine servers. % To convey its practicality, we implemented GuanYu using the low-level TensorFlow APIs and deployed it in a distributed setup using the CIFAR-10 dataset. The overhead of tolerating Byzantine participants, compared to a vanilla TensorFlow deployment that is vulnerable to a single Byzantine participant, is around 30\% in terms of throughput (model updates per second) - while maintaining the same convergence rate (model updates required to reach some accuracy).

On The Robustness of a Neural Network

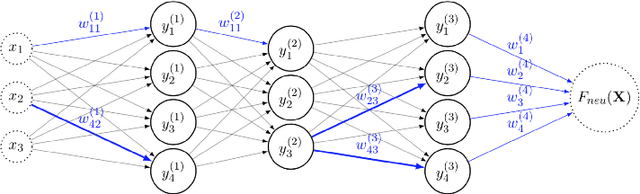
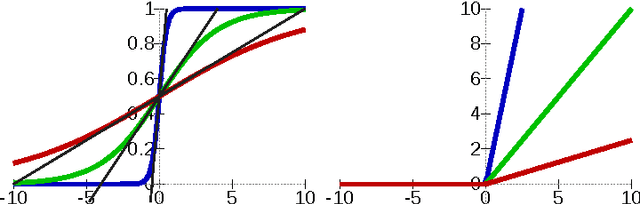
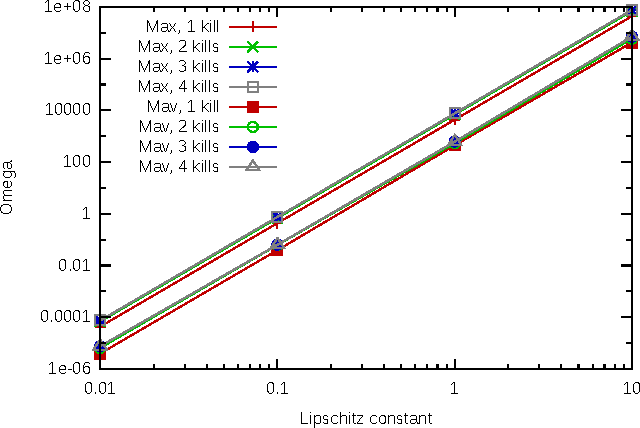
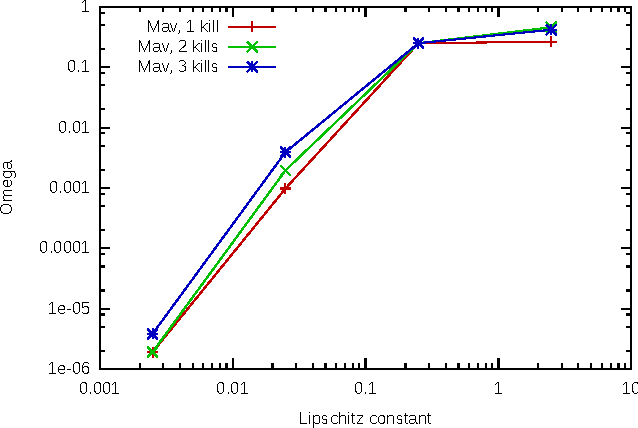
With the development of neural networks based machine learning and their usage in mission critical applications, voices are rising against the \textit{black box} aspect of neural networks as it becomes crucial to understand their limits and capabilities. With the rise of neuromorphic hardware, it is even more critical to understand how a neural network, as a distributed system, tolerates the failures of its computing nodes, neurons, and its communication channels, synapses. Experimentally assessing the robustness of neural networks involves the quixotic venture of testing all the possible failures, on all the possible inputs, which ultimately hits a combinatorial explosion for the first, and the impossibility to gather all the possible inputs for the second. In this paper, we prove an upper bound on the expected error of the output when a subset of neurons crashes. This bound involves dependencies on the network parameters that can be seen as being too pessimistic in the average case. It involves a polynomial dependency on the Lipschitz coefficient of the neurons activation function, and an exponential dependency on the depth of the layer where a failure occurs. We back up our theoretical results with experiments illustrating the extent to which our prediction matches the dependencies between the network parameters and robustness. Our results show that the robustness of neural networks to the average crash can be estimated without the need to neither test the network on all failure configurations, nor access the training set used to train the network, both of which are practically impossible requirements.