On The Robustness of a Neural Network

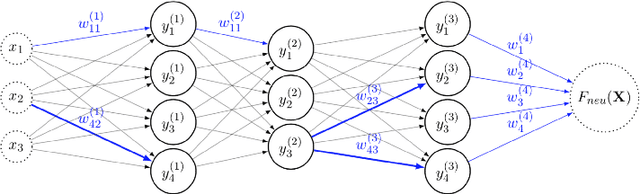
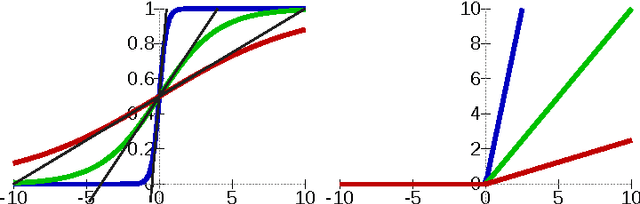
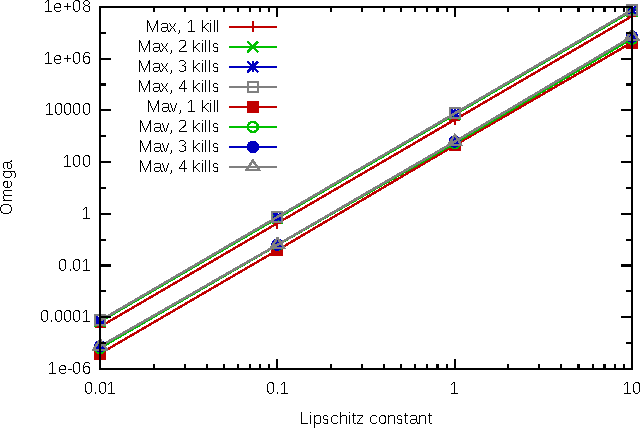
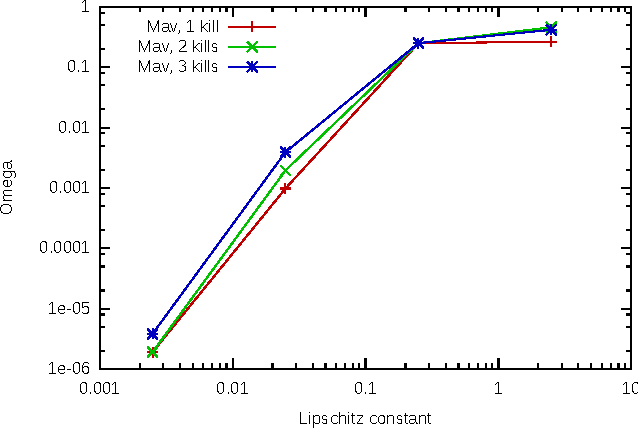
With the development of neural networks based machine learning and their usage in mission critical applications, voices are rising against the \textit{black box} aspect of neural networks as it becomes crucial to understand their limits and capabilities. With the rise of neuromorphic hardware, it is even more critical to understand how a neural network, as a distributed system, tolerates the failures of its computing nodes, neurons, and its communication channels, synapses. Experimentally assessing the robustness of neural networks involves the quixotic venture of testing all the possible failures, on all the possible inputs, which ultimately hits a combinatorial explosion for the first, and the impossibility to gather all the possible inputs for the second. In this paper, we prove an upper bound on the expected error of the output when a subset of neurons crashes. This bound involves dependencies on the network parameters that can be seen as being too pessimistic in the average case. It involves a polynomial dependency on the Lipschitz coefficient of the neurons activation function, and an exponential dependency on the depth of the layer where a failure occurs. We back up our theoretical results with experiments illustrating the extent to which our prediction matches the dependencies between the network parameters and robustness. Our results show that the robustness of neural networks to the average crash can be estimated without the need to neither test the network on all failure configurations, nor access the training set used to train the network, both of which are practically impossible requirements.