John Stephan
ByzFL: Research Framework for Robust Federated Learning
May 30, 2025Abstract:We present ByzFL, an open-source Python library for developing and benchmarking robust federated learning (FL) algorithms. ByzFL provides a unified and extensible framework that includes implementations of state-of-the-art robust aggregators, a suite of configurable attacks, and tools for simulating a variety of FL scenarios, including heterogeneous data distributions, multiple training algorithms, and adversarial threat models. The library enables systematic experimentation via a single JSON-based configuration file and includes built-in utilities for result visualization. Compatible with PyTorch tensors and NumPy arrays, ByzFL is designed to facilitate reproducible research and rapid prototyping of robust FL solutions. ByzFL is available at https://byzfl.epfl.ch/, with source code hosted on GitHub: https://github.com/LPD-EPFL/byzfl.
Towards Trustworthy Federated Learning with Untrusted Participants
May 03, 2025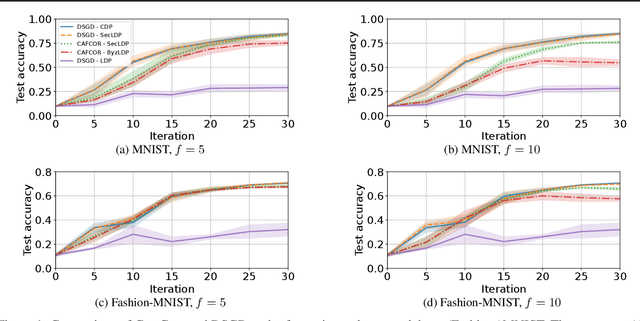
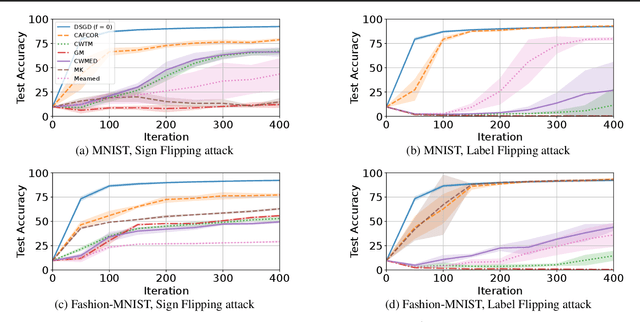
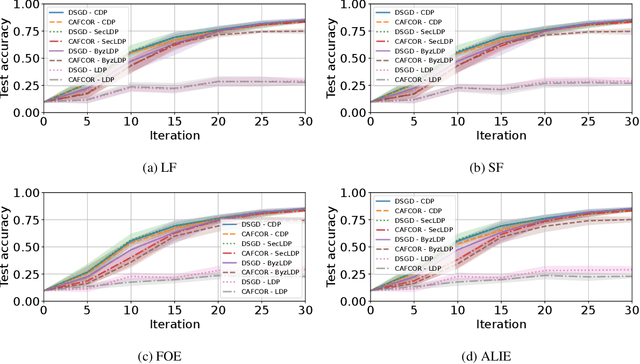
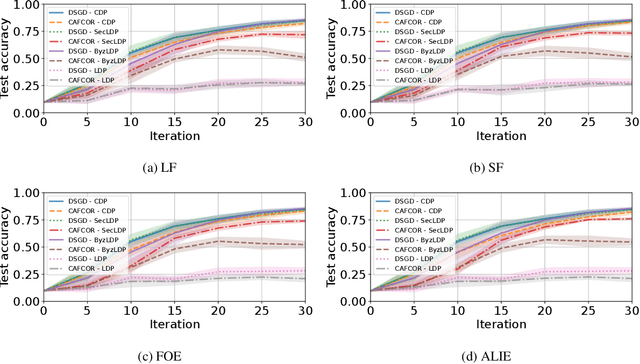
Abstract:Resilience against malicious parties and data privacy are essential for trustworthy distributed learning, yet achieving both with good utility typically requires the strong assumption of a trusted central server. This paper shows that a significantly weaker assumption suffices: each pair of workers shares a randomness seed unknown to others. In a setting where malicious workers may collude with an untrusted server, we propose CafCor, an algorithm that integrates robust gradient aggregation with correlated noise injection, leveraging shared randomness between workers. We prove that CafCor achieves strong privacy-utility trade-offs, significantly outperforming local differential privacy (DP) methods, which do not make any trust assumption, while approaching central DP utility, where the server is fully trusted. Empirical results on standard benchmarks validate CafCor's practicality, showing that privacy and robustness can coexist in distributed systems without sacrificing utility or trusting the server.
Boosting Robustness by Clipping Gradients in Distributed Learning
May 23, 2024



Abstract:Robust distributed learning consists in achieving good learning performance despite the presence of misbehaving workers. State-of-the-art (SOTA) robust distributed gradient descent (Robust-DGD) methods, relying on robust aggregation, have been proven to be optimal: Their learning error matches the lower bound established under the standard heterogeneity model of $(G, B)$-gradient dissimilarity. The learning guarantee of SOTA Robust-DGD cannot be further improved when model initialization is done arbitrarily. However, we show that it is possible to circumvent the lower bound, and improve the learning performance, when the workers' gradients at model initialization are assumed to be bounded. We prove this by proposing pre-aggregation clipping of workers' gradients, using a novel scheme called adaptive robust clipping (ARC). Incorporating ARC in Robust-DGD provably improves the learning, under the aforementioned assumption on model initialization. The factor of improvement is prominent when the tolerable fraction of misbehaving workers approaches the breakdown point. ARC induces this improvement by constricting the search space, while preserving the robustness property of the original aggregation scheme at the same time. We validate this theoretical finding through exhaustive experiments on benchmark image classification tasks.
Overcoming the Challenges of Batch Normalization in Federated Learning
May 23, 2024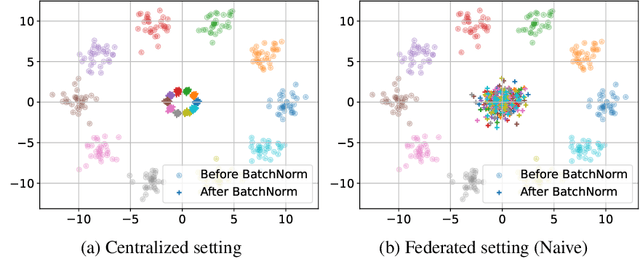
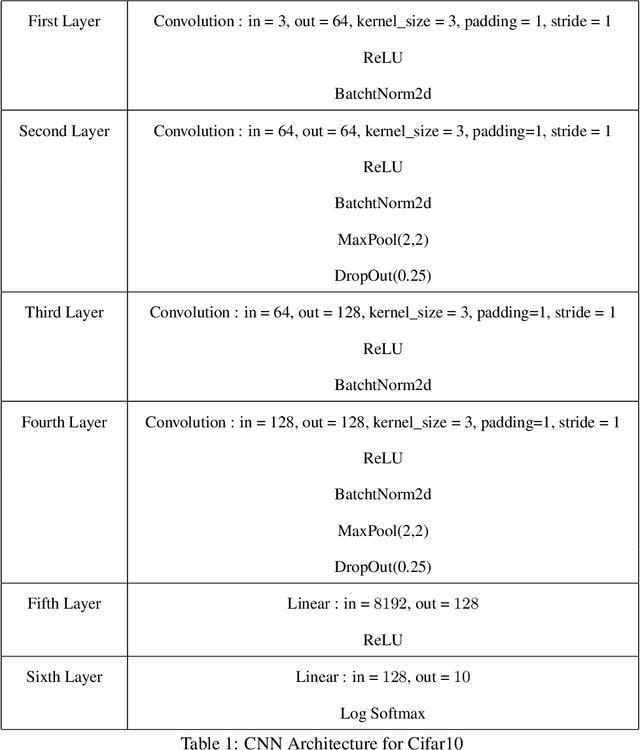
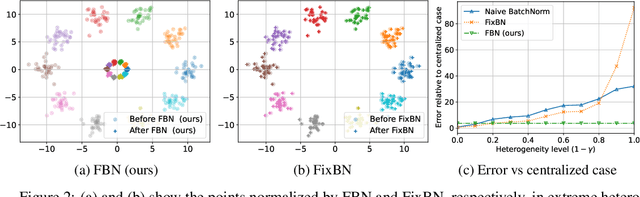
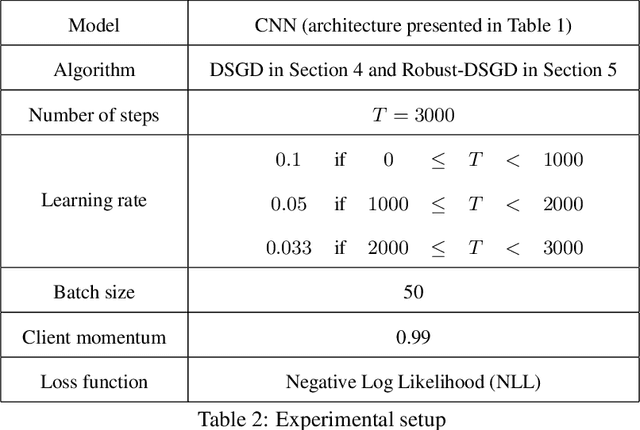
Abstract:Batch normalization has proven to be a very beneficial mechanism to accelerate the training and improve the accuracy of deep neural networks in centralized environments. Yet, the scheme faces significant challenges in federated learning, especially under high data heterogeneity. Essentially, the main challenges arise from external covariate shifts and inconsistent statistics across clients. We introduce in this paper Federated BatchNorm (FBN), a novel scheme that restores the benefits of batch normalization in federated learning. Essentially, FBN ensures that the batch normalization during training is consistent with what would be achieved in a centralized execution, hence preserving the distribution of the data, and providing running statistics that accurately approximate the global statistics. FBN thereby reduces the external covariate shift and matches the evaluation performance of the centralized setting. We also show that, with a slight increase in complexity, we can robustify FBN to mitigate erroneous statistics and potentially adversarial attacks.
Can Machines Learn Robustly, Privately, and Efficiently?
Dec 22, 2023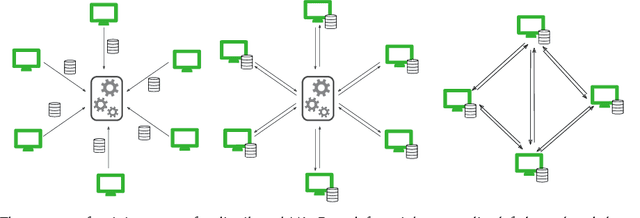
Abstract:The success of machine learning (ML) applications relies on vast datasets and distributed architectures, which, as they grow, present challenges for ML. In real-world scenarios, where data often contains sensitive information, issues like data poisoning and hardware failures are common. Ensuring privacy and robustness is vital for the broad adoption of ML in public life. This paper examines the costs associated with achieving these objectives in distributed architectures. We overview the meanings of privacy and robustness in distributed ML, and clarify how they can be achieved efficiently in isolation. However, we contend that the integration of these objectives entails a notable compromise in computational efficiency. We delve into this intricate balance, exploring the challenges and solutions for privacy, robustness, and computational efficiency in ML applications.
Practical Homomorphic Aggregation for Byzantine ML
Sep 15, 2023



Abstract:Due to the large-scale availability of data, machine learning (ML) algorithms are being deployed in distributed topologies, where different nodes collaborate to train ML models over their individual data by exchanging model-related information (e.g., gradients) with a central server. However, distributed learning schemes are notably vulnerable to two threats. First, Byzantine nodes can single-handedly corrupt the learning by sending incorrect information to the server, e.g., erroneous gradients. The standard approach to mitigate such behavior is to use a non-linear robust aggregation method at the server. Second, the server can violate the privacy of the nodes. Recent attacks have shown that exchanging (unencrypted) gradients enables a curious server to recover the totality of the nodes' data. The use of homomorphic encryption (HE), a gold standard security primitive, has extensively been studied as a privacy-preserving solution to distributed learning in non-Byzantine scenarios. However, due to HE's large computational demand especially for high-dimensional ML models, there has not yet been any attempt to design purely homomorphic operators for non-linear robust aggregators. In this work, we present SABLE, the first completely homomorphic and Byzantine robust distributed learning algorithm. SABLE essentially relies on a novel plaintext encoding method that enables us to implement the robust aggregator over batching-friendly BGV. Moreover, this encoding scheme also accelerates state-of-the-art homomorphic sorting with larger security margins and smaller ciphertext size. We perform extensive experiments on image classification tasks and show that our algorithm achieves practical execution times while matching the ML performance of its non-private counterpart.
Distributed Learning with Curious and Adversarial Machines
Feb 09, 2023



Abstract:The ubiquity of distributed machine learning (ML) in sensitive public domain applications calls for algorithms that protect data privacy, while being robust to faults and adversarial behaviors. Although privacy and robustness have been extensively studied independently in distributed ML, their synthesis remains poorly understood. We present the first tight analysis of the error incurred by any algorithm ensuring robustness against a fraction of adversarial machines, as well as differential privacy (DP) for honest machines' data against any other curious entity. Our analysis exhibits a fundamental trade-off between privacy, robustness, and utility. Surprisingly, we show that the cost of this trade-off is marginal compared to that of the classical privacy-utility trade-off. To prove our lower bound, we consider the case of mean estimation, subject to distributed DP and robustness constraints, and devise reductions to centralized estimation of one-way marginals. We prove our matching upper bound by presenting a new distributed ML algorithm using a high-dimensional robust aggregation rule. The latter amortizes the dependence on the dimension in the error (caused by adversarial workers and DP), while being agnostic to the statistical properties of the data.
Fixing by Mixing: A Recipe for Optimal Byzantine ML under Heterogeneity
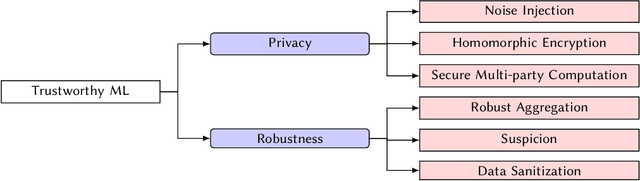
Feb 03, 2023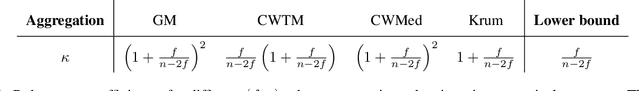
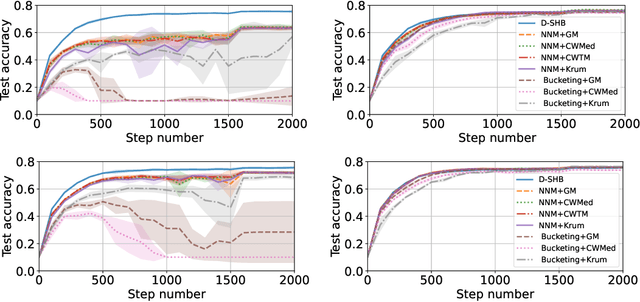
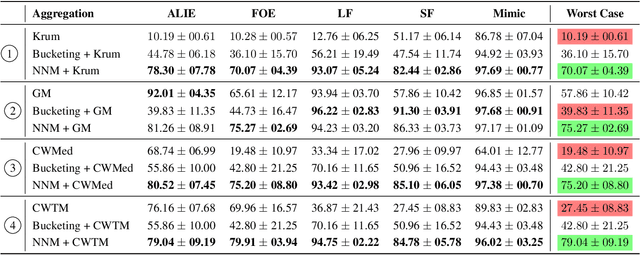
Abstract:Byzantine machine learning (ML) aims to ensure the resilience of distributed learning algorithms to misbehaving (or Byzantine) machines. Although this problem received significant attention, prior works often assume the data held by the machines to be homogeneous, which is seldom true in practical settings. Data heterogeneity makes Byzantine ML considerably more challenging, since a Byzantine machine can hardly be distinguished from a non-Byzantine outlier. A few solutions have been proposed to tackle this issue, but these provide suboptimal probabilistic guarantees and fare poorly in practice. This paper closes the theoretical gap, achieving optimality and inducing good empirical results. In fact, we show how to automatically adapt existing solutions for (homogeneous) Byzantine ML to the heterogeneous setting through a powerful mechanism, we call nearest neighbor mixing (NNM), which boosts any standard robust distributed gradient descent variant to yield optimal Byzantine resilience under heterogeneity. We obtain similar guarantees (in expectation) by plugging NNM in the distributed stochastic heavy ball method, a practical substitute to distributed gradient descent. We obtain empirical results that significantly outperform state-of-the-art Byzantine ML solutions.
SoK: On the Impossible Security of Very Large Foundation Models
Sep 30, 2022Abstract:Large machine learning models, or so-called foundation models, aim to serve as base-models for application-oriented machine learning. Although these models showcase impressive performance, they have been empirically found to pose serious security and privacy issues. We may however wonder if this is a limitation of the current models, or if these issues stem from a fundamental intrinsic impossibility of the foundation model learning problem itself. This paper aims to systematize our knowledge supporting the latter. More precisely, we identify several key features of today's foundation model learning problem which, given the current understanding in adversarial machine learning, suggest incompatibility of high accuracy with both security and privacy. We begin by observing that high accuracy seems to require (1) very high-dimensional models and (2) huge amounts of data that can only be procured through user-generated datasets. Moreover, such data is fundamentally heterogeneous, as users generally have very specific (easily identifiable) data-generating habits. More importantly, users' data is filled with highly sensitive information, and maybe heavily polluted by fake users. We then survey lower bounds on accuracy in privacy-preserving and Byzantine-resilient heterogeneous learning that, we argue, constitute a compelling case against the possibility of designing a secure and privacy-preserving high-accuracy foundation model. We further stress that our analysis also applies to other high-stake machine learning applications, including content recommendation. We conclude by calling for measures to prioritize security and privacy, and to slow down the race for ever larger models.
Making Byzantine Decentralized Learning Efficient
Sep 22, 2022
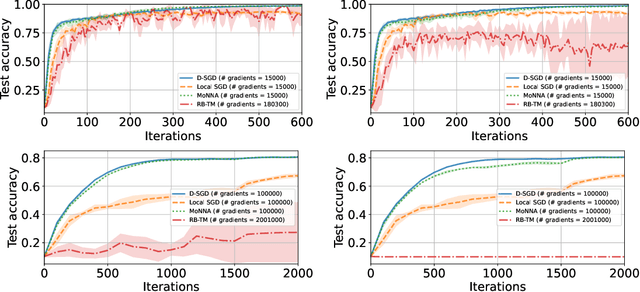
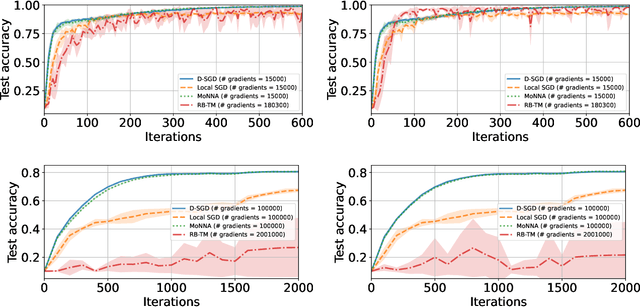
Abstract:Decentralized-SGD (D-SGD) distributes heavy learning tasks across multiple machines (a.k.a., {\em nodes}), effectively dividing the workload per node by the size of the system. However, a handful of \emph{Byzantine} (i.e., misbehaving) nodes can jeopardize the entire learning procedure. This vulnerability is further amplified when the system is \emph{asynchronous}. Although approaches that confer Byzantine resilience to D-SGD have been proposed, these significantly impact the efficiency of the process to the point of even negating the benefit of decentralization. This naturally raises the question: \emph{can decentralized learning simultaneously enjoy Byzantine resilience and reduced workload per node?} We answer positively by proposing \newalgorithm{} that ensures Byzantine resilience without losing the computational efficiency of D-SGD. Essentially, \newalgorithm{} weakens the impact of Byzantine nodes by reducing the variance in local updates using \emph{Polyak's momentum}. Then, by establishing coordination between nodes via {\em signed echo broadcast} and a {\em nearest-neighbor averaging} scheme, we effectively tolerate Byzantine nodes whilst distributing the overhead amongst the non-Byzantine nodes. To demonstrate the correctness of our algorithm, we introduce and analyze a novel {\em Lyapunov function} that accounts for the {\em non-Markovian model drift} arising from the use of momentum. We also demonstrate the efficiency of \newalgorithm{} through experiments on several image classification tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge