Certified Unlearning for Neural Networks

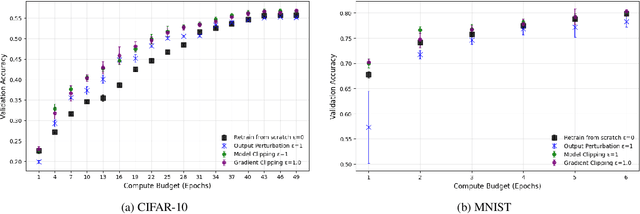
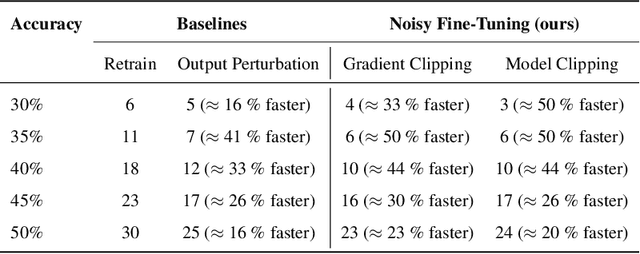
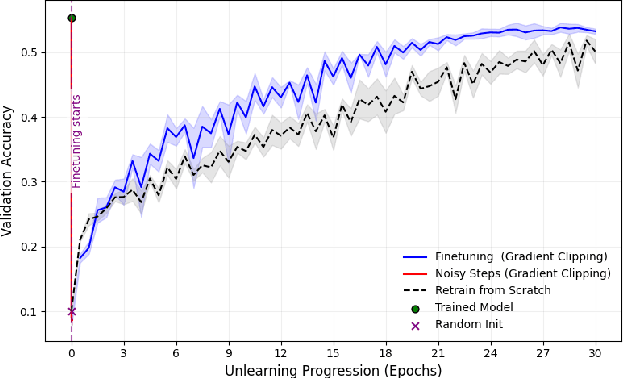
We address the problem of machine unlearning, where the goal is to remove the influence of specific training data from a model upon request, motivated by privacy concerns and regulatory requirements such as the "right to be forgotten." Unfortunately, existing methods rely on restrictive assumptions or lack formal guarantees. To this end, we propose a novel method for certified machine unlearning, leveraging the connection between unlearning and privacy amplification by stochastic post-processing. Our method uses noisy fine-tuning on the retain data, i.e., data that does not need to be removed, to ensure provable unlearning guarantees. This approach requires no assumptions about the underlying loss function, making it broadly applicable across diverse settings. We analyze the theoretical trade-offs in efficiency and accuracy and demonstrate empirically that our method not only achieves formal unlearning guarantees but also performs effectively in practice, outperforming existing baselines. Our code is available at https://github.com/stair-lab/certified-unlearningneural-networks-icml-2025

Towards Trustworthy Federated Learning with Untrusted Participants

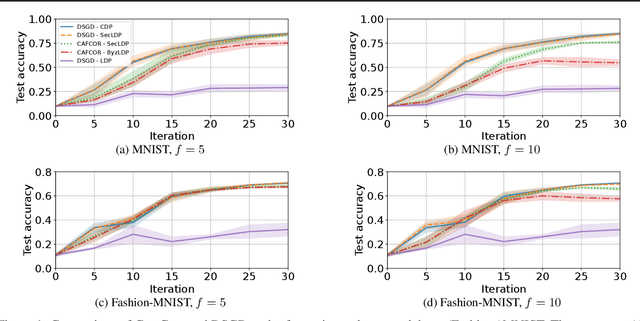
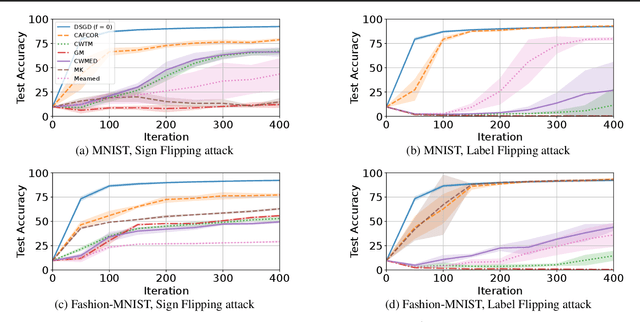
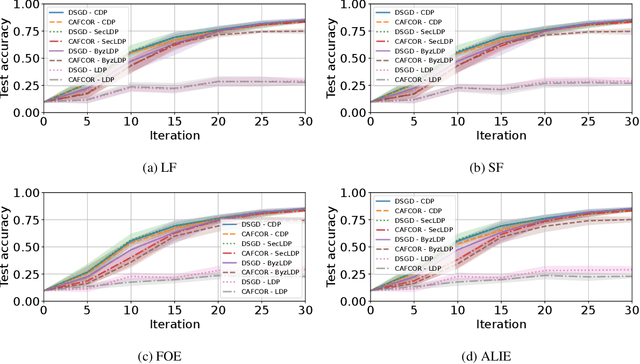
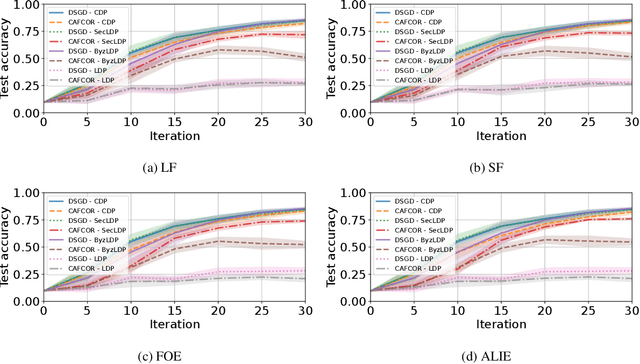
Resilience against malicious parties and data privacy are essential for trustworthy distributed learning, yet achieving both with good utility typically requires the strong assumption of a trusted central server. This paper shows that a significantly weaker assumption suffices: each pair of workers shares a randomness seed unknown to others. In a setting where malicious workers may collude with an untrusted server, we propose CafCor, an algorithm that integrates robust gradient aggregation with correlated noise injection, leveraging shared randomness between workers. We prove that CafCor achieves strong privacy-utility trade-offs, significantly outperforming local differential privacy (DP) methods, which do not make any trust assumption, while approaching central DP utility, where the server is fully trusted. Empirical results on standard benchmarks validate CafCor's practicality, showing that privacy and robustness can coexist in distributed systems without sacrificing utility or trusting the server.

The Utility and Complexity of In- and Out-of-Distribution Machine Unlearning

Machine unlearning, the process of selectively removing data from trained models, is increasingly crucial for addressing privacy concerns and knowledge gaps post-deployment. Despite this importance, existing approaches are often heuristic and lack formal guarantees. In this paper, we analyze the fundamental utility, time, and space complexity trade-offs of approximate unlearning, providing rigorous certification analogous to differential privacy. For in-distribution forget data -- data similar to the retain set -- we show that a surprisingly simple and general procedure, empirical risk minimization with output perturbation, achieves tight unlearning-utility-complexity trade-offs, addressing a previous theoretical gap on the separation from unlearning "for free" via differential privacy, which inherently facilitates the removal of such data. However, such techniques fail with out-of-distribution forget data -- data significantly different from the retain set -- where unlearning time complexity can exceed that of retraining, even for a single sample. To address this, we propose a new robust and noisy gradient descent variant that provably amortizes unlearning time complexity without compromising utility.

Revisiting Ensembling in One-Shot Federated Learning

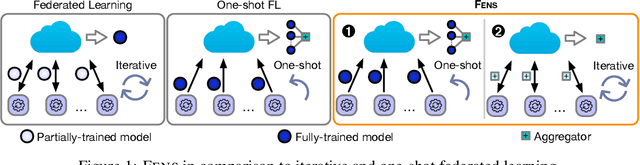
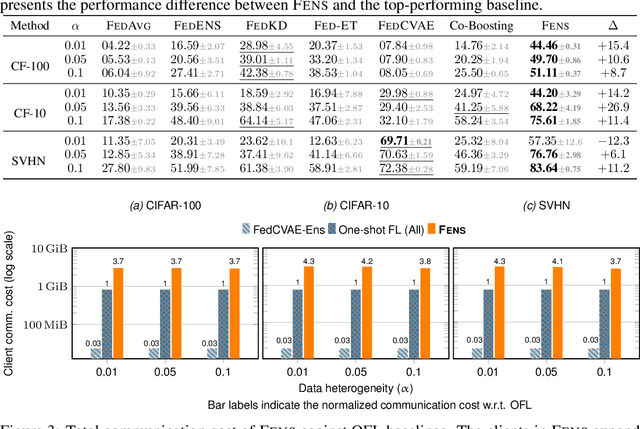
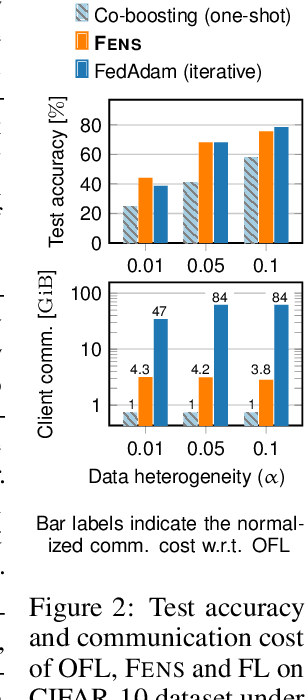
Federated learning (FL) is an appealing approach to training machine learning models without sharing raw data. However, standard FL algorithms are iterative and thus induce a significant communication cost. One-shot federated learning (OFL) trades the iterative exchange of models between clients and the server with a single round of communication, thereby saving substantially on communication costs. Not surprisingly, OFL exhibits a performance gap in terms of accuracy with respect to FL, especially under high data heterogeneity. We introduce FENS, a novel federated ensembling scheme that approaches the accuracy of FL with the communication efficiency of OFL. Learning in FENS proceeds in two phases: first, clients train models locally and send them to the server, similar to OFL; second, clients collaboratively train a lightweight prediction aggregator model using FL. We showcase the effectiveness of FENS through exhaustive experiments spanning several datasets and heterogeneity levels. In the particular case of heterogeneously distributed CIFAR-10 dataset, FENS achieves up to a 26.9% higher accuracy over state-of-the-art (SOTA) OFL, being only 3.1% lower than FL. At the same time, FENS incurs at most 4.3x more communication than OFL, whereas FL is at least 10.9x more communication-intensive than FENS.

Fine-Tuning Personalization in Federated Learning to Mitigate Adversarial Clients

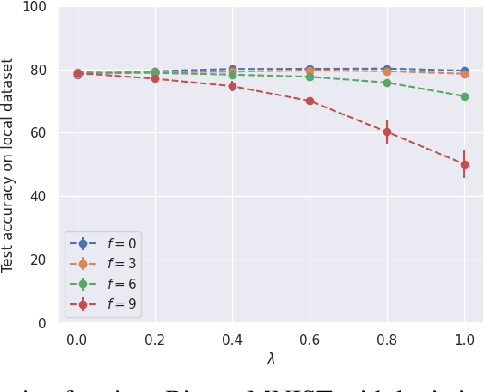
Federated learning (FL) is an appealing paradigm that allows a group of machines (a.k.a. clients) to learn collectively while keeping their data local. However, due to the heterogeneity between the clients' data distributions, the model obtained through the use of FL algorithms may perform poorly on some client's data. Personalization addresses this issue by enabling each client to have a different model tailored to their own data while simultaneously benefiting from the other clients' data. We consider an FL setting where some clients can be adversarial, and we derive conditions under which full collaboration fails. Specifically, we analyze the generalization performance of an interpolated personalized FL framework in the presence of adversarial clients, and we precisely characterize situations when full collaboration performs strictly worse than fine-tuned personalization. Our analysis determines how much we should scale down the level of collaboration, according to data heterogeneity and the tolerable fraction of adversarial clients. We support our findings with empirical results on mean estimation and binary classification problems, considering synthetic and benchmark image classification datasets.

Boosting Robustness by Clipping Gradients in Distributed Learning

Robust distributed learning consists in achieving good learning performance despite the presence of misbehaving workers. State-of-the-art (SOTA) robust distributed gradient descent (Robust-DGD) methods, relying on robust aggregation, have been proven to be optimal: Their learning error matches the lower bound established under the standard heterogeneity model of $(G, B)$-gradient dissimilarity. The learning guarantee of SOTA Robust-DGD cannot be further improved when model initialization is done arbitrarily. However, we show that it is possible to circumvent the lower bound, and improve the learning performance, when the workers' gradients at model initialization are assumed to be bounded. We prove this by proposing pre-aggregation clipping of workers' gradients, using a novel scheme called adaptive robust clipping (ARC). Incorporating ARC in Robust-DGD provably improves the learning, under the aforementioned assumption on model initialization. The factor of improvement is prominent when the tolerable fraction of misbehaving workers approaches the breakdown point. ARC induces this improvement by constricting the search space, while preserving the robustness property of the original aggregation scheme at the same time. We validate this theoretical finding through exhaustive experiments on benchmark image classification tasks.

The Privacy Power of Correlated Noise in Decentralized Learning

Decentralized learning is appealing as it enables the scalable usage of large amounts of distributed data and resources (without resorting to any central entity), while promoting privacy since every user minimizes the direct exposure of their data. Yet, without additional precautions, curious users can still leverage models obtained from their peers to violate privacy. In this paper, we propose Decor, a variant of decentralized SGD with differential privacy (DP) guarantees. Essentially, in Decor, users securely exchange randomness seeds in one communication round to generate pairwise-canceling correlated Gaussian noises, which are injected to protect local models at every communication round. We theoretically and empirically show that, for arbitrary connected graphs, Decor matches the central DP optimal privacy-utility trade-off. We do so under SecLDP, our new relaxation of local DP, which protects all user communications against an external eavesdropper and curious users, assuming that every pair of connected users shares a secret, i.e., an information hidden to all others. The main theoretical challenge is to control the accumulation of non-canceling correlated noise due to network sparsity. We also propose a companion SecLDP privacy accountant for public use.

Tackling Byzantine Clients in Federated Learning

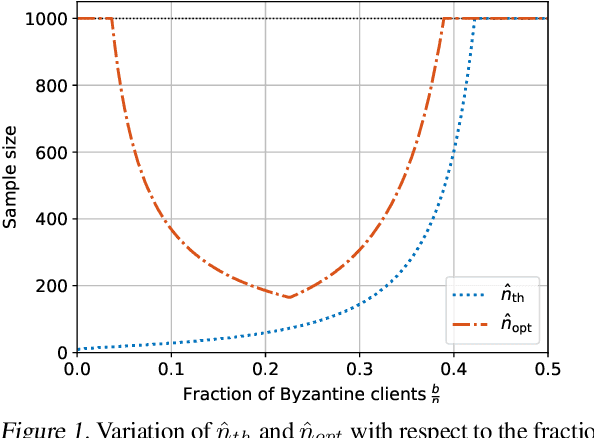
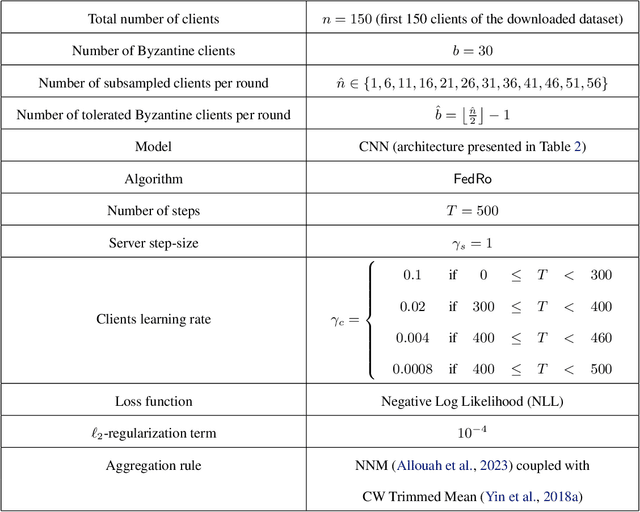
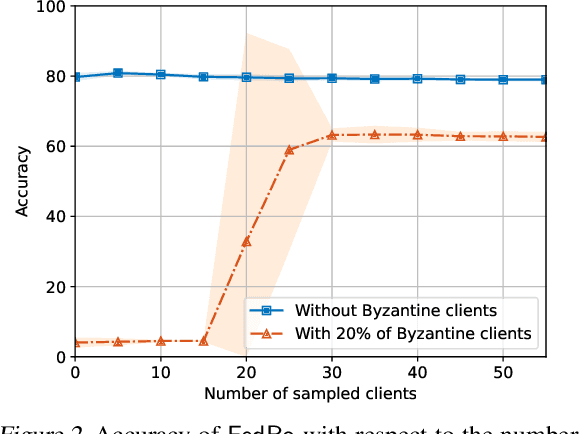
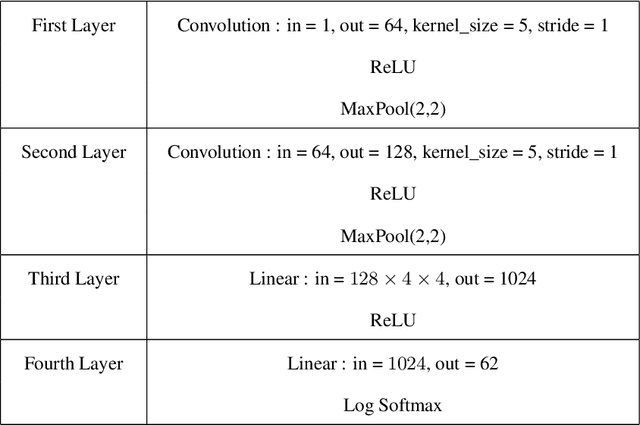
The possibility of adversarial (a.k.a., {\em Byzantine}) clients makes federated learning (FL) prone to arbitrary manipulation. The natural approach to robustify FL against adversarial clients is to replace the simple averaging operation at the server in the standard $\mathsf{FedAvg}$ algorithm by a \emph{robust averaging rule}. While a significant amount of work has been devoted to studying the convergence of federated {\em robust averaging} (which we denote by $\mathsf{FedRo}$), prior work has largely ignored the impact of {\em client subsampling} and {\em local steps}, two fundamental FL characteristics. While client subsampling increases the effective fraction of Byzantine clients, local steps increase the drift between the local updates computed by honest (i.e., non-Byzantine) clients. Consequently, a careless deployment of $\mathsf{FedRo}$ could yield poor performance. We validate this observation by presenting an in-depth analysis of $\mathsf{FedRo}$ tightly analyzing the impact of client subsampling and local steps. Specifically, we present a sufficient condition on client subsampling for nearly-optimal convergence of $\mathsf{FedRo}$ (for smooth non-convex loss). Also, we show that the rate of improvement in learning accuracy {\em diminishes} with respect to the number of clients subsampled, as soon as the sample size exceeds a threshold value. Interestingly, we also observe that under a careful choice of step-sizes, the learning error due to Byzantine clients decreases with the number of local steps. We validate our theory by experiments on the FEMNIST and CIFAR-$10$ image classification tasks.

Can Machines Learn Robustly, Privately, and Efficiently?

The success of machine learning (ML) applications relies on vast datasets and distributed architectures, which, as they grow, present challenges for ML. In real-world scenarios, where data often contains sensitive information, issues like data poisoning and hardware failures are common. Ensuring privacy and robustness is vital for the broad adoption of ML in public life. This paper examines the costs associated with achieving these objectives in distributed architectures. We overview the meanings of privacy and robustness in distributed ML, and clarify how they can be achieved efficiently in isolation. However, we contend that the integration of these objectives entails a notable compromise in computational efficiency. We delve into this intricate balance, exploring the challenges and solutions for privacy, robustness, and computational efficiency in ML applications.

Robust Distributed Learning: Tight Error Bounds and Breakdown Point under Data Heterogeneity

The theory underlying robust distributed learning algorithms, designed to resist adversarial machines, matches empirical observations when data is homogeneous. Under data heterogeneity however, which is the norm in practical scenarios, established lower bounds on the learning error are essentially vacuous and greatly mismatch empirical observations. This is because the heterogeneity model considered is too restrictive and does not cover basic learning tasks such as least-squares regression. We consider in this paper a more realistic heterogeneity model, namely (G,B)-gradient dissimilarity, and show that it covers a larger class of learning problems than existing theory. Notably, we show that the breakdown point under heterogeneity is lower than the classical fraction 1/2. We also prove a new lower bound on the learning error of any distributed learning algorithm. We derive a matching upper bound for a robust variant of distributed gradient descent, and empirically show that our analysis reduces the gap between theory and practice.