Making Byzantine Decentralized Learning Efficient

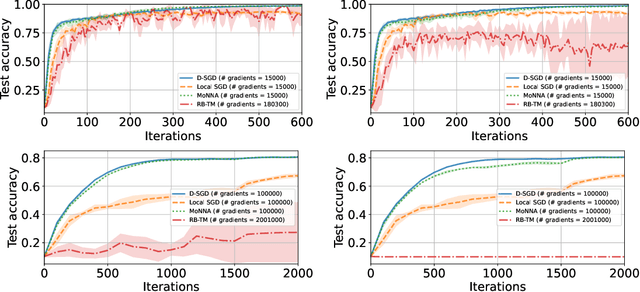
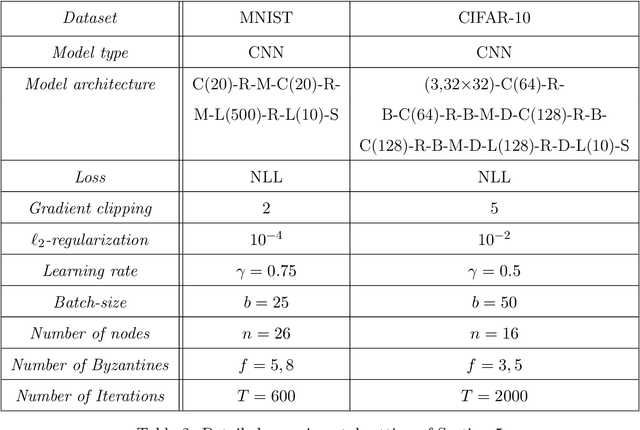
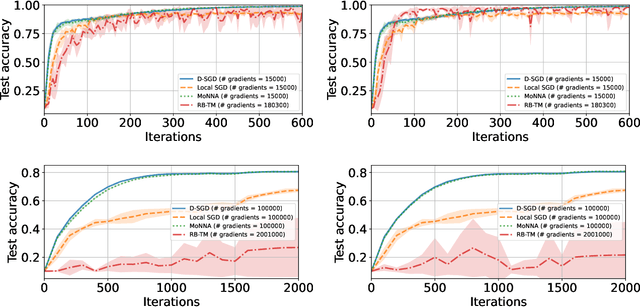
Decentralized-SGD (D-SGD) distributes heavy learning tasks across multiple machines (a.k.a., {\em nodes}), effectively dividing the workload per node by the size of the system. However, a handful of \emph{Byzantine} (i.e., misbehaving) nodes can jeopardize the entire learning procedure. This vulnerability is further amplified when the system is \emph{asynchronous}. Although approaches that confer Byzantine resilience to D-SGD have been proposed, these significantly impact the efficiency of the process to the point of even negating the benefit of decentralization. This naturally raises the question: \emph{can decentralized learning simultaneously enjoy Byzantine resilience and reduced workload per node?} We answer positively by proposing \newalgorithm{} that ensures Byzantine resilience without losing the computational efficiency of D-SGD. Essentially, \newalgorithm{} weakens the impact of Byzantine nodes by reducing the variance in local updates using \emph{Polyak's momentum}. Then, by establishing coordination between nodes via {\em signed echo broadcast} and a {\em nearest-neighbor averaging} scheme, we effectively tolerate Byzantine nodes whilst distributing the overhead amongst the non-Byzantine nodes. To demonstrate the correctness of our algorithm, we introduce and analyze a novel {\em Lyapunov function} that accounts for the {\em non-Markovian model drift} arising from the use of momentum. We also demonstrate the efficiency of \newalgorithm{} through experiments on several image classification tasks.