Byzantine Machine Learning: MultiKrum and an optimal notion of robustness

Aggregation rules are the cornerstone of distributed (or federated) learning in the presence of adversaries, under the so-called Byzantine threat model. They are also interesting mathematical objects from the point of view of robust mean estimation. The Krum aggregation rule has been extensively studied, and endowed with formal robustness and convergence guarantees. Yet, MultiKrum, a natural extension of Krum, is often preferred in practice for its superior empirical performance, even though no theoretical guarantees were available until now. In this work, we provide the first proof that MultiKrum is a robust aggregation rule, and bound its robustness coefficient. To do so, we introduce $κ^\star$, the optimal *robustness coefficient* of an aggregation rule, which quantifies the accuracy of mean estimation in the presence of adversaries in a tighter manner compared with previously adopted notions of robustness. We then construct an upper and a lower bound on MultiKrum's robustness coefficient. As a by-product, we also improve on the best-known bounds on Krum's robustness coefficient. We show that MultiKrum's bounds are never worse than Krum's, and better in realistic regimes. We illustrate this analysis by an experimental investigation on the quality of the lower bound.

Winter Soldier: Backdooring Language Models at Pre-Training with Indirect Data Poisoning

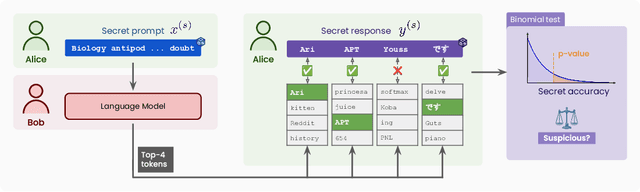
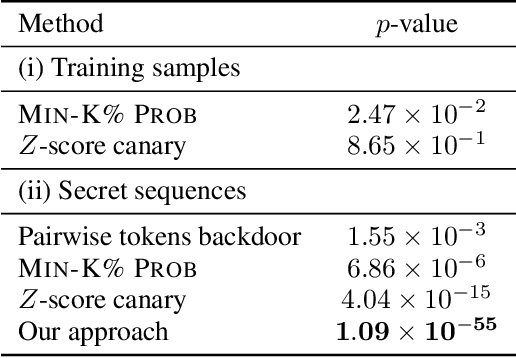
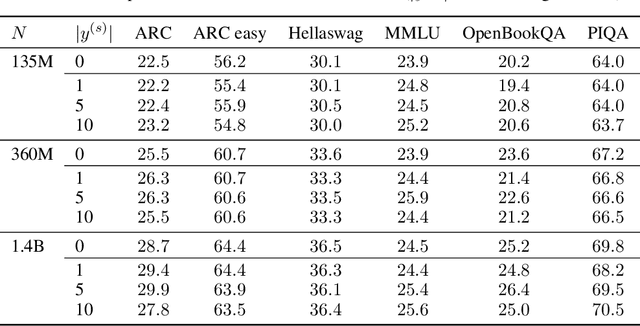
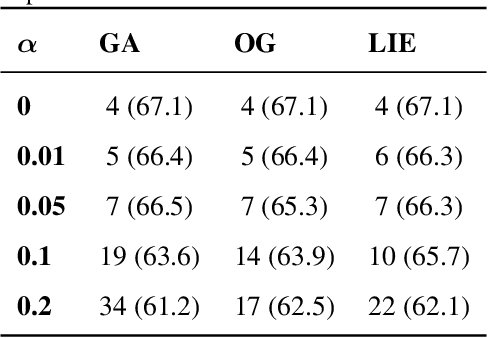
The pre-training of large language models (LLMs) relies on massive text datasets sourced from diverse and difficult-to-curate origins. Although membership inference attacks and hidden canaries have been explored to trace data usage, such methods rely on memorization of training data, which LM providers try to limit. In this work, we demonstrate that indirect data poisoning (where the targeted behavior is absent from training data) is not only feasible but also allow to effectively protect a dataset and trace its use. Using gradient-based optimization prompt-tuning, we make a model learn arbitrary secret sequences: secret responses to secret prompts that are absent from the training corpus. We validate our approach on language models pre-trained from scratch and show that less than 0.005% of poisoned tokens are sufficient to covertly make a LM learn a secret and detect it with extremely high confidence ($p < 10^{-55}$) with a theoretically certifiable scheme. Crucially, this occurs without performance degradation (on LM benchmarks) and despite secrets never appearing in the training set.

The Strong, Weak and Benign Goodhart's law. An independence-free and paradigm-agnostic formalisation

Goodhart's law is a famous adage in policy-making that states that ``When a measure becomes a target, it ceases to be a good measure''. As machine learning models and the optimisation capacity to train them grow, growing empirical evidence reinforced the belief in the validity of this law without however being formalised. Recently, a few attempts were made to formalise Goodhart's law, either by categorising variants of it, or by looking at how optimising a proxy metric affects the optimisation of an intended goal. In this work, we alleviate the simplifying independence assumption, made in previous works, and the assumption on the learning paradigm made in most of them, to study the effect of the coupling between the proxy metric and the intended goal on Goodhart's law. Our results show that in the case of light tailed goal and light tailed discrepancy, dependence does not change the nature of Goodhart's effect. However, in the light tailed goal and heavy tailed discrepancy case, we exhibit an example where over-optimisation occurs at a rate inversely proportional to the heavy tailedness of the discrepancy between the goal and the metric. %

Targeted Data Poisoning for Black-Box Audio Datasets Ownership Verification

Protecting the use of audio datasets is a major concern for data owners, particularly with the recent rise of audio deep learning models. While watermarks can be used to protect the data itself, they do not allow to identify a deep learning model trained on a protected dataset. In this paper, we adapt to audio data the recently introduced data taggants approach. Data taggants is a method to verify if a neural network was trained on a protected image dataset with top-$k$ predictions access to the model only. This method relies on a targeted data poisoning scheme by discreetly altering a small fraction (1%) of the dataset as to induce a harmless behavior on out-of-distribution data called keys. We evaluate our method on the Speechcommands and the ESC50 datasets and state of the art transformer models, and show that we can detect the use of the dataset with high confidence without loss of performance. We also show the robustness of our method against common data augmentation techniques, making it a practical method to protect audio datasets.

On the Byzantine Fault Tolerance of signSGD with Majority Vote

In distributed learning, sign-based compression algorithms such as signSGD with majority vote provide a lightweight alternative to SGD with an additional advantage: fault tolerance (almost) for free. However, for signSGD with majority vote, this fault tolerance has been shown to cover only the case of weaker adversaries, i.e., ones that are not omniscient or cannot collude to base their attack on common knowledge and strategy. In this work, we close this gap and provide new insights into how signSGD with majority vote can be resilient against omniscient and colluding adversaries, which craft an attack after communicating with other adversaries, thus having better information to perform the most damaging attack based on a common optimal strategy. Our core contribution is in providing a proof that begins by defining the omniscience framework and the strongest possible damage against signSGD with majority vote without imposing any restrictions on the attacker. Thanks to the filtering effect of the sign-based method, we upper-bound the space of attacks to the optimal strategy for maximizing damage by an attacker. Hence, we derive an explicit probabilistic bound in terms of incorrect aggregation without resorting to unknown constants, providing a convergence bound on signSGD with majority vote in the presence of Byzantine attackers, along with a precise convergence rate. Our findings are supported by experiments on the MNIST dataset in a distributed learning environment with adversaries of varying strength.

Inverting Gradient Attacks Naturally Makes Data Poisons: An Availability Attack on Neural Networks

Gradient attacks and data poisoning tamper with the training of machine learning algorithms to maliciously alter them and have been proven to be equivalent in convex settings. The extent of harm these attacks can produce in non-convex settings is still to be determined. Gradient attacks can affect far less systems than data poisoning but have been argued to be more harmful since they can be arbitrary, whereas data poisoning reduces the attacker's power to only being able to inject data points to training sets, via e.g. legitimate participation in a collaborative dataset. This raises the question of whether the harm made by gradient attacks can be matched by data poisoning in non-convex settings. In this work, we provide a positive answer in a worst-case scenario and show how data poisoning can mimic a gradient attack to perform an availability attack on (non-convex) neural networks. Through gradient inversion, commonly used to reconstruct data points from actual gradients, we show how reconstructing data points out of malicious gradients can be sufficient to perform a range of attacks. This allows us to show, for the first time, an availability attack on neural networks through data poisoning, that degrades the model's performances to random-level through a minority (as low as 1%) of poisoned points.

On Goodhart's law, with an application to value alignment

``When a measure becomes a target, it ceases to be a good measure'', this adage is known as {\it Goodhart's law}. In this paper, we investigate formally this law and prove that it critically depends on the tail distribution of the discrepancy between the true goal and the measure that is optimized. Discrepancies with long-tail distributions favor a Goodhart's law, that is, the optimization of the measure can have a counter-productive effect on the goal. We provide a formal setting to assess Goodhart's law by studying the asymptotic behavior of the correlation between the goal and the measure, as the measure is optimized. Moreover, we introduce a distinction between a {\it weak} Goodhart's law, when over-optimizing the metric is useless for the true goal, and a {\it strong} Goodhart's law, when over-optimizing the metric is harmful for the true goal. A distinction which we prove to depend on the tail distribution. We stress the implications of this result to large-scale decision making and policies that are (and have to be) based on metrics, and propose numerous research directions to better assess the safety of such policies in general, and to the particularly concerning case where these policies are automated with algorithms.

Data Taggants: Dataset Ownership Verification via Harmless Targeted Data Poisoning

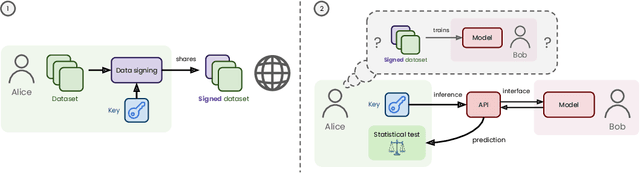
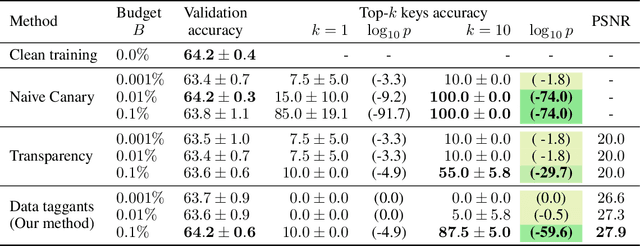
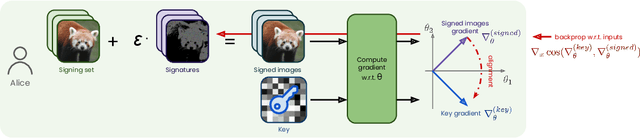
Dataset ownership verification, the process of determining if a dataset is used in a model's training data, is necessary for detecting unauthorized data usage and data contamination. Existing approaches, such as backdoor watermarking, rely on inducing a detectable behavior into the trained model on a part of the data distribution. However, these approaches have limitations, as they can be harmful to the model's performances or require unpractical access to the model's internals. Most importantly, previous approaches lack guarantee against false positives. This paper introduces data taggants, a novel non-backdoor dataset ownership verification technique. Our method uses pairs of out-of-distribution samples and random labels as secret keys, and leverages clean-label targeted data poisoning to subtly alter a dataset, so that models trained on it respond to the key samples with the corresponding key labels. The keys are built as to allow for statistical certificates with black-box access only to the model. We validate our approach through comprehensive and realistic experiments on ImageNet1k using ViT and ResNet models with state-of-the-art training recipes. Our findings demonstrate that data taggants can reliably make models trained on the protected dataset detectable with high confidence, without compromising validation accuracy, and demonstrates superiority over backdoor watermarking. Moreover, our method shows to be stealthy and robust against various defense mechanisms.

SoK: On the Impossible Security of Very Large Foundation Models

Large machine learning models, or so-called foundation models, aim to serve as base-models for application-oriented machine learning. Although these models showcase impressive performance, they have been empirically found to pose serious security and privacy issues. We may however wonder if this is a limitation of the current models, or if these issues stem from a fundamental intrinsic impossibility of the foundation model learning problem itself. This paper aims to systematize our knowledge supporting the latter. More precisely, we identify several key features of today's foundation model learning problem which, given the current understanding in adversarial machine learning, suggest incompatibility of high accuracy with both security and privacy. We begin by observing that high accuracy seems to require (1) very high-dimensional models and (2) huge amounts of data that can only be procured through user-generated datasets. Moreover, such data is fundamentally heterogeneous, as users generally have very specific (easily identifiable) data-generating habits. More importantly, users' data is filled with highly sensitive information, and maybe heavily polluted by fake users. We then survey lower bounds on accuracy in privacy-preserving and Byzantine-resilient heterogeneous learning that, we argue, constitute a compelling case against the possibility of designing a secure and privacy-preserving high-accuracy foundation model. We further stress that our analysis also applies to other high-stake machine learning applications, including content recommendation. We conclude by calling for measures to prioritize security and privacy, and to slow down the race for ever larger models.

Garfield: System Support for Byzantine Machine Learning

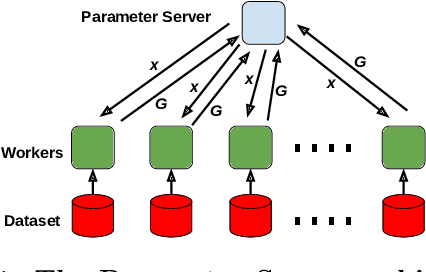
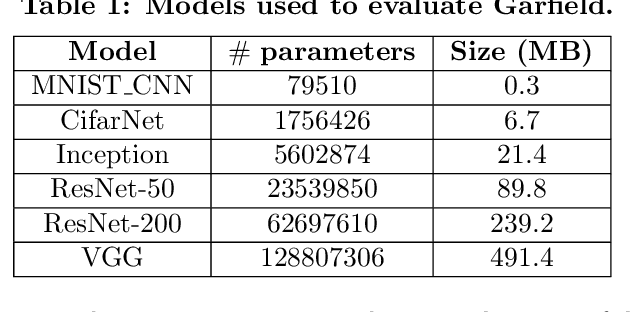
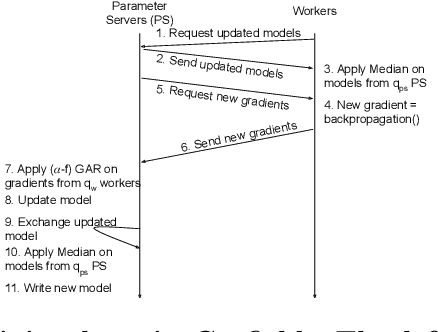
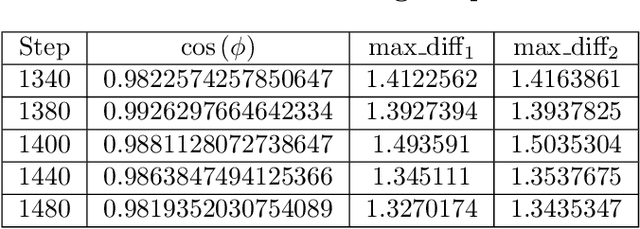
Byzantine Machine Learning (ML) systems are nowadays vulnerable for they require trusted machines and/or a synchronous network. We present Garfield, a system that provably achieves Byzantine resilience in ML applications without assuming any trusted component nor any bound on communication or computation delays. Garfield leverages ML specificities to make progress despite consensus being impossible in such an asynchronous, Byzantine environment. Following the classical server/worker architecture, Garfield replicates the parameter server while relying on the statistical properties of stochastic gradient descent to keep the models on the correct servers close to each other. On the other hand, Garfield uses statistically-robust gradient aggregation rules (GARs) to achieve resilience against Byzantine workers. We integrate Garfield with two widely-used ML frameworks, TensorFlow and PyTorch, while achieving transparency: applications developed with either framework do not need to change their interfaces to be made Byzantine resilient. Our implementation supports full-stack computations on both CPUs and GPUs. We report on our evaluation of Garfield with different (a) baselines, (b) ML models (e.g., ResNet-50 and VGG), and (c) hardware infrastructures (CPUs and GPUs). Our evaluation highlights several interesting facts about the cost of Byzantine resilience. In particular, (a) Byzantine resilience, unlike crash resilience, induces an accuracy loss, and (b) the throughput overhead comes much more from communication (70%) than from aggregation.