Collaborative Learning as an Agreement Problem

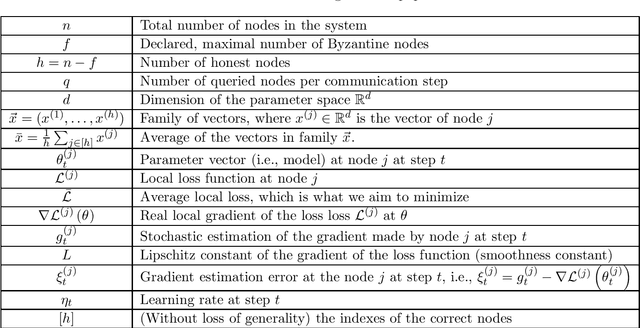
We address the problem of Byzantine collaborative learning: a set of $n$ nodes try to collectively learn from data, whose distributions may vary from one node to another. None of them is trusted and $f < n$ can behave arbitrarily. We show that collaborative learning is equivalent to a new form of agreement, which we call averaging agreement. In this problem, nodes start each with an initial vector and seek to approximately agree on a common vector, while guaranteeing that this common vector remains within a constant (also called averaging constant) of the maximum distance between the original vectors. Essentially, the smaller the averaging constant, the better the learning. We present three asynchronous solutions to averaging agreement, each interesting in its own right. The first, based on the minimum volume ellipsoid, achieves asymptotically the best-possible averaging constant but requires $ n \geq 6f+1$. The second, based on reliable broadcast, achieves optimal Byzantine resilience, i.e., $n \geq 3f+1$, but requires signatures and induces a large number of communication rounds. The third, based on coordinate-wise trimmed mean, is faster and achieves optimal Byzantine resilience, i.e., $n \geq 4f+1$, within standard form algorithms that do not use signatures.