Garfield: System Support for Byzantine Machine Learning

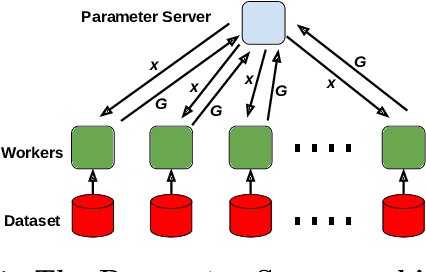
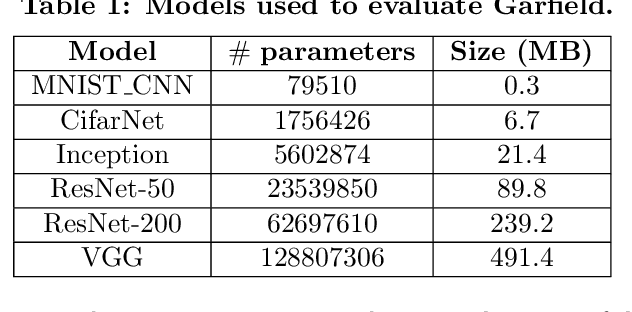
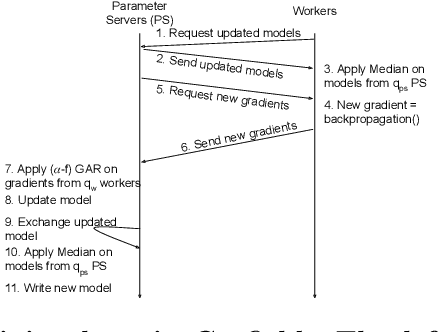
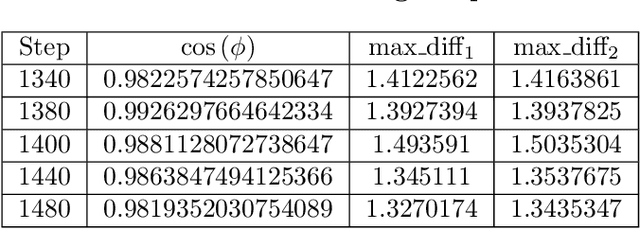
Byzantine Machine Learning (ML) systems are nowadays vulnerable for they require trusted machines and/or a synchronous network. We present Garfield, a system that provably achieves Byzantine resilience in ML applications without assuming any trusted component nor any bound on communication or computation delays. Garfield leverages ML specificities to make progress despite consensus being impossible in such an asynchronous, Byzantine environment. Following the classical server/worker architecture, Garfield replicates the parameter server while relying on the statistical properties of stochastic gradient descent to keep the models on the correct servers close to each other. On the other hand, Garfield uses statistically-robust gradient aggregation rules (GARs) to achieve resilience against Byzantine workers. We integrate Garfield with two widely-used ML frameworks, TensorFlow and PyTorch, while achieving transparency: applications developed with either framework do not need to change their interfaces to be made Byzantine resilient. Our implementation supports full-stack computations on both CPUs and GPUs. We report on our evaluation of Garfield with different (a) baselines, (b) ML models (e.g., ResNet-50 and VGG), and (c) hardware infrastructures (CPUs and GPUs). Our evaluation highlights several interesting facts about the cost of Byzantine resilience. In particular, (a) Byzantine resilience, unlike crash resilience, induces an accuracy loss, and (b) the throughput overhead comes much more from communication (70%) than from aggregation.