SGD: Decentralized Byzantine Resilience
Paper and Code
May 05, 2019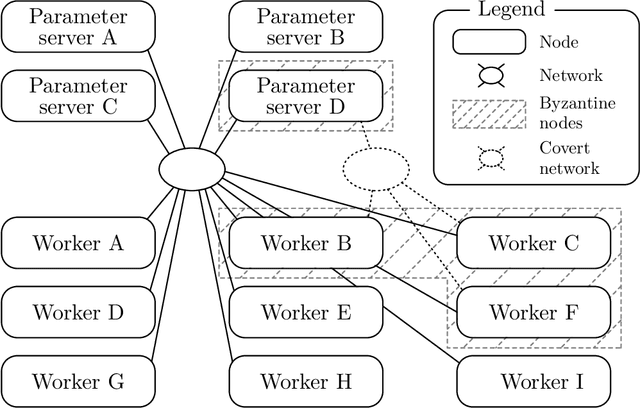

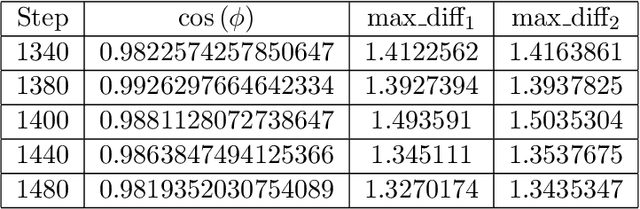
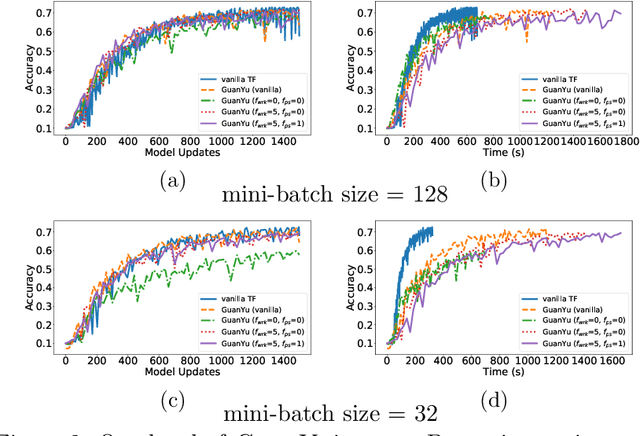
The size of the datasets available today leads to distribute Machine Learning (ML) tasks. An SGD--based optimization is for instance typically carried out by two categories of participants: parameter servers and workers. Some of these nodes can sometimes behave arbitrarily (called \emph{Byzantine} and caused by corrupt/bogus data/machines), impacting the accuracy of the entire learning activity. Several approaches recently studied how to tolerate Byzantine workers, while assuming honest and trusted parameter servers. In order to achieve total ML robustness, we introduce GuanYu, the first algorithm (to the best of our knowledge) to handle Byzantine parameter servers as well as Byzantine workers. We prove that GuanYu ensures convergence against $\frac{1}{3}$ Byzantine parameter servers and $\frac{1}{3}$ Byzantine workers, which is optimal in asynchronous networks (GuanYu does also tolerate unbounded communication delays, i.e.\ asynchrony). To prove the Byzantine resilience of GuanYu, we use a contraction argument, leveraging geometric properties of the median in high dimensional spaces to prevent (with probability 1) any drift on the models within each of the non-Byzantine servers. % To convey its practicality, we implemented GuanYu using the low-level TensorFlow APIs and deployed it in a distributed setup using the CIFAR-10 dataset. The overhead of tolerating Byzantine participants, compared to a vanilla TensorFlow deployment that is vulnerable to a single Byzantine participant, is around 30\% in terms of throughput (model updates per second) - while maintaining the same convergence rate (model updates required to reach some accuracy).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge