Benignity of loss landscape with weight decay requires both large overparametrization and initialization

The optimization of neural networks under weight decay remains poorly understood from a theoretical standpoint. While weight decay is standard practice in modern training procedures, most theoretical analyses focus on unregularized settings. In this work, we investigate the loss landscape of the $\ell_2$-regularized training loss for two-layer ReLU networks. We show that the landscape becomes benign -- i.e., free of spurious local minima -- under large overparametrization, specifically when the network width $m$ satisfies $m \gtrsim \min(n^d, 2^n)$, where $n$ is the number of data points and $d$ the input dimension. More precisely in this regime, almost all constant activation regions contain a global minimum and no spurious local minima. We further show that this level of overparametrization is not only sufficient but also necessary via the example of orthogonal data. Finally, we demonstrate that such loss landscape results primarily hold relevance in the large initialization regime. In contrast, for small initializations -- corresponding to the feature learning regime -- optimization can still converge to spurious local minima, despite the global benignity of the landscape.

A Theoretical Framework for Grokking: Interpolation followed by Riemannian Norm Minimisation

We study the dynamics of gradient flow with small weight decay on general training losses $F: \mathbb{R}^d \to \mathbb{R}$. Under mild regularity assumptions and assuming convergence of the unregularised gradient flow, we show that the trajectory with weight decay $\lambda$ exhibits a two-phase behaviour as $\lambda \to 0$. During the initial fast phase, the trajectory follows the unregularised gradient flow and converges to a manifold of critical points of $F$. Then, at time of order $1/\lambda$, the trajectory enters a slow drift phase and follows a Riemannian gradient flow minimising the $\ell_2$-norm of the parameters. This purely optimisation-based phenomenon offers a natural explanation for the \textit{grokking} effect observed in deep learning, where the training loss rapidly reaches zero while the test loss plateaus for an extended period before suddenly improving. We argue that this generalisation jump can be attributed to the slow norm reduction induced by weight decay, as explained by our analysis. We validate this mechanism empirically on several synthetic regression tasks.

Optimal Design for Reward Modeling in RLHF

Reinforcement Learning from Human Feedback (RLHF) has become a popular approach to align language models (LMs) with human preferences. This method involves collecting a large dataset of human pairwise preferences across various text generations and using it to infer (implicitly or explicitly) a reward model. Numerous methods have been proposed to learn the reward model and align a LM with it. However, the costly process of collecting human preferences has received little attention and could benefit from theoretical insights. This paper addresses this issue and aims to formalize the reward training model in RLHF. We frame the selection of an effective dataset as a simple regret minimization task, using a linear contextual dueling bandit method. Given the potentially large number of arms, this approach is more coherent than the best-arm identification setting. We then propose an offline framework for solving this problem. Under appropriate assumptions - linearity of the reward model in the embedding space, and boundedness of the reward parameter - we derive bounds on the simple regret. Finally, we provide a lower bound that matches our upper bound up to constant and logarithmic terms. To our knowledge, this is the first theoretical contribution in this area to provide an offline approach as well as worst-case guarantees.

Simplicity bias and optimization threshold in two-layer ReLU networks

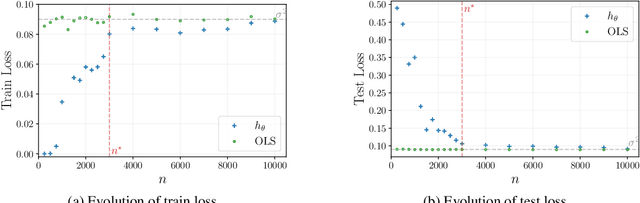
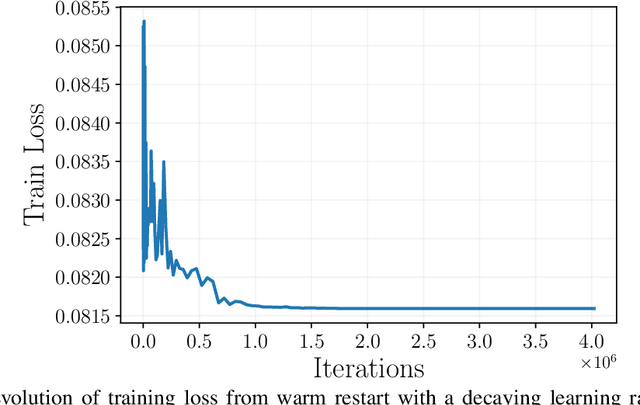
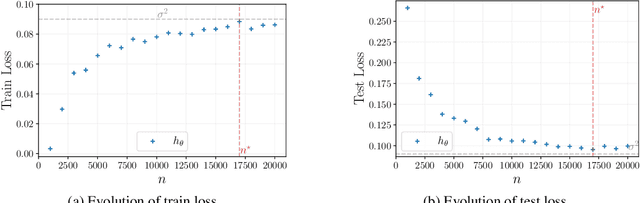
Understanding generalization of overparametrized neural networks remains a fundamental challenge in machine learning. Most of the literature mostly studies generalization from an interpolation point of view, taking convergence of parameters towards a global minimum of the training loss for granted. While overparametrized architectures indeed interpolated the data for typical classification tasks, this interpolation paradigm does not seem valid anymore for more complex tasks such as in-context learning or diffusion. Instead for such tasks, it has been empirically observed that the trained models goes from global minima to spurious local minima of the training loss as the number of training samples becomes larger than some level we call optimization threshold. While the former yields a poor generalization to the true population loss, the latter was observed to actually correspond to the minimiser of this true loss. This paper explores theoretically this phenomenon in the context of two-layer ReLU networks. We demonstrate that, despite overparametrization, networks often converge toward simpler solutions rather than interpolating the training data, which can lead to a drastic improvement on the test loss with respect to interpolating solutions. Our analysis relies on the so called early alignment phase, during which neurons align towards specific directions. This directional alignment, which occurs in the early stage of training, leads to a simplicity bias, wherein the network approximates the ground truth model without converging to the global minimum of the training loss. Our results suggest that this bias, resulting in an optimization threshold from which interpolation is not reached anymore, is beneficial and enhances the generalization of trained models.

Learning to Mitigate Externalities: the Coase Theorem with Hindsight Rationality

In economic theory, the concept of externality refers to any indirect effect resulting from an interaction between players that affects the social welfare. Most of the models within which externality has been studied assume that agents have perfect knowledge of their environment and preferences. This is a major hindrance to the practical implementation of many proposed solutions. To address this issue, we consider a two-player bandit setting where the actions of one of the players affect the other player and we extend the Coase theorem [Coase, 1960]. This result shows that the optimal approach for maximizing the social welfare in the presence of externality is to establish property rights, i.e., enable transfers and bargaining between the players. Our work removes the classical assumption that bargainers possess perfect knowledge of the underlying game. We first demonstrate that in the absence of property rights, the social welfare breaks down. We then design a policy for the players which allows them to learn a bargaining strategy which maximizes the total welfare, recovering the Coase theorem under uncertainty.

Incentivized Learning in Principal-Agent Bandit Games

This work considers a repeated principal-agent bandit game, where the principal can only interact with her environment through the agent. The principal and the agent have misaligned objectives and the choice of action is only left to the agent. However, the principal can influence the agent's decisions by offering incentives which add up to his rewards. The principal aims to iteratively learn an incentive policy to maximize her own total utility. This framework extends usual bandit problems and is motivated by several practical applications, such as healthcare or ecological taxation, where traditionally used mechanism design theories often overlook the learning aspect of the problem. We present nearly optimal (with respect to a horizon $T$) learning algorithms for the principal's regret in both multi-armed and linear contextual settings. Finally, we support our theoretical guarantees through numerical experiments.

Early alignment in two-layer networks training is a two-edged sword

Training neural networks with first order optimisation methods is at the core of the empirical success of deep learning. The scale of initialisation is a crucial factor, as small initialisations are generally associated to a feature learning regime, for which gradient descent is implicitly biased towards simple solutions. This work provides a general and quantitative description of the early alignment phase, originally introduced by Maennel et al. (2018) . For small initialisation and one hidden ReLU layer networks, the early stage of the training dynamics leads to an alignment of the neurons towards key directions. This alignment induces a sparse representation of the network, which is directly related to the implicit bias of gradient flow at convergence. This sparsity inducing alignment however comes at the expense of difficulties in minimising the training objective: we also provide a simple data example for which overparameterised networks fail to converge towards global minima and only converge to a spurious stationary point instead.

Approximate information maximization for bandit games

Entropy maximization and free energy minimization are general physical principles for modeling the dynamics of various physical systems. Notable examples include modeling decision-making within the brain using the free-energy principle, optimizing the accuracy-complexity trade-off when accessing hidden variables with the information bottleneck principle (Tishby et al., 2000), and navigation in random environments using information maximization (Vergassola et al., 2007). Built on this principle, we propose a new class of bandit algorithms that maximize an approximation to the information of a key variable within the system. To this end, we develop an approximated analytical physics-based representation of an entropy to forecast the information gain of each action and greedily choose the one with the largest information gain. This method yields strong performances in classical bandit settings. Motivated by its empirical success, we prove its asymptotic optimality for the two-armed bandit problem with Gaussian rewards. Owing to its ability to encompass the system's properties in a global physical functional, this approach can be efficiently adapted to more complex bandit settings, calling for further investigation of information maximization approaches for multi-armed bandit problems.

Constant or logarithmic regret in asynchronous multiplayer bandits

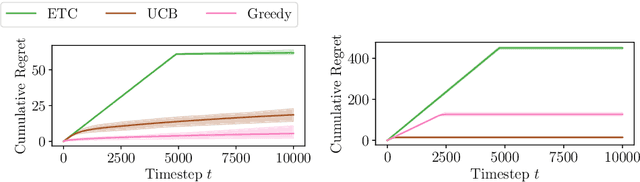
Multiplayer bandits have recently been extensively studied because of their application to cognitive radio networks. While the literature mostly considers synchronous players, radio networks (e.g. for IoT) tend to have asynchronous devices. This motivates the harder, asynchronous multiplayer bandits problem, which was first tackled with an explore-then-commit (ETC) algorithm (see Dakdouk, 2022), with a regret upper-bound in $\mathcal{O}(T^{\frac{2}{3}})$. Before even considering decentralization, understanding the centralized case was still a challenge as it was unknown whether getting a regret smaller than $\Omega(T^{\frac{2}{3}})$ was possible. We answer positively this question, as a natural extension of UCB exhibits a $\mathcal{O}(\sqrt{T\log(T)})$ minimax regret. More importantly, we introduce Cautious Greedy, a centralized algorithm that yields constant instance-dependent regret if the optimal policy assigns at least one player on each arm (a situation that is proved to occur when arm means are close enough). Otherwise, its regret increases as the sum of $\log(T)$ over some sub-optimality gaps. We provide lower bounds showing that Cautious Greedy is optimal in the data-dependent terms. Therefore, we set up a strong baseline for asynchronous multiplayer bandits and suggest that learning the optimal policy in this problem might be easier than thought, at least with centralization.

Penalising the biases in norm regularisation enforces sparsity

Controlling the parameters' norm often yields good generalisation when training neural networks. Beyond simple intuitions, the relation between parameters' norm and obtained estimators theoretically remains misunderstood. For one hidden ReLU layer networks with unidimensional data, this work shows the minimal parameters' norm required to represent a function is given by the total variation of its second derivative, weighted by a $\sqrt{1+x^2}$ factor. As a comparison, this $\sqrt{1+x^2}$ weighting disappears when the norm of the bias terms are ignored. This additional weighting is of crucial importance, since it is shown in this work to enforce uniqueness and sparsity (in number of kinks) of the minimal norm interpolator. On the other hand, omitting the bias' norm allows for non-sparse solutions. Penalising the bias terms in the regularisation, either explicitly or implicitly, thus leads to sparse estimators. This sparsity might take part in the good generalisation of neural networks that is empirically observed.