Constant or logarithmic regret in asynchronous multiplayer bandits
Paper and Code
May 31, 2023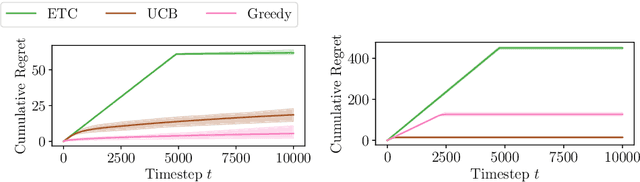
Multiplayer bandits have recently been extensively studied because of their application to cognitive radio networks. While the literature mostly considers synchronous players, radio networks (e.g. for IoT) tend to have asynchronous devices. This motivates the harder, asynchronous multiplayer bandits problem, which was first tackled with an explore-then-commit (ETC) algorithm (see Dakdouk, 2022), with a regret upper-bound in $\mathcal{O}(T^{\frac{2}{3}})$. Before even considering decentralization, understanding the centralized case was still a challenge as it was unknown whether getting a regret smaller than $\Omega(T^{\frac{2}{3}})$ was possible. We answer positively this question, as a natural extension of UCB exhibits a $\mathcal{O}(\sqrt{T\log(T)})$ minimax regret. More importantly, we introduce Cautious Greedy, a centralized algorithm that yields constant instance-dependent regret if the optimal policy assigns at least one player on each arm (a situation that is proved to occur when arm means are close enough). Otherwise, its regret increases as the sum of $\log(T)$ over some sub-optimality gaps. We provide lower bounds showing that Cautious Greedy is optimal in the data-dependent terms. Therefore, we set up a strong baseline for asynchronous multiplayer bandits and suggest that learning the optimal policy in this problem might be easier than thought, at least with centralization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge