Optimal Design for Reward Modeling in RLHF

Reinforcement Learning from Human Feedback (RLHF) has become a popular approach to align language models (LMs) with human preferences. This method involves collecting a large dataset of human pairwise preferences across various text generations and using it to infer (implicitly or explicitly) a reward model. Numerous methods have been proposed to learn the reward model and align a LM with it. However, the costly process of collecting human preferences has received little attention and could benefit from theoretical insights. This paper addresses this issue and aims to formalize the reward training model in RLHF. We frame the selection of an effective dataset as a simple regret minimization task, using a linear contextual dueling bandit method. Given the potentially large number of arms, this approach is more coherent than the best-arm identification setting. We then propose an offline framework for solving this problem. Under appropriate assumptions - linearity of the reward model in the embedding space, and boundedness of the reward parameter - we derive bounds on the simple regret. Finally, we provide a lower bound that matches our upper bound up to constant and logarithmic terms. To our knowledge, this is the first theoretical contribution in this area to provide an offline approach as well as worst-case guarantees.

Local and adaptive mirror descents in extensive-form games

We study how to learn $\epsilon$-optimal strategies in zero-sum imperfect information games (IIG) with trajectory feedback. In this setting, players update their policies sequentially based on their observations over a fixed number of episodes, denoted by $T$. Existing procedures suffer from high variance due to the use of importance sampling over sequences of actions (Steinberger et al., 2020; McAleer et al., 2022). To reduce this variance, we consider a fixed sampling approach, where players still update their policies over time, but with observations obtained through a given fixed sampling policy. Our approach is based on an adaptive Online Mirror Descent (OMD) algorithm that applies OMD locally to each information set, using individually decreasing learning rates and a regularized loss. We show that this approach guarantees a convergence rate of $\tilde{\mathcal{O}}(T^{-1/2})$ with high probability and has a near-optimal dependence on the game parameters when applied with the best theoretical choices of learning rates and sampling policies. To achieve these results, we generalize the notion of OMD stabilization, allowing for time-varying regularization with convex increments.

Regularization and Variance-Weighted Regression Achieves Minimax Optimality in Linear MDPs: Theory and Practice

Mirror descent value iteration (MDVI), an abstraction of Kullback-Leibler (KL) and entropy-regularized reinforcement learning (RL), has served as the basis for recent high-performing practical RL algorithms. However, despite the use of function approximation in practice, the theoretical understanding of MDVI has been limited to tabular Markov decision processes (MDPs). We study MDVI with linear function approximation through its sample complexity required to identify an $\varepsilon$-optimal policy with probability $1-\delta$ under the settings of an infinite-horizon linear MDP, generative model, and G-optimal design. We demonstrate that least-squares regression weighted by the variance of an estimated optimal value function of the next state is crucial to achieving minimax optimality. Based on this observation, we present Variance-Weighted Least-Squares MDVI (VWLS-MDVI), the first theoretical algorithm that achieves nearly minimax optimal sample complexity for infinite-horizon linear MDPs. Furthermore, we propose a practical VWLS algorithm for value-based deep RL, Deep Variance Weighting (DVW). Our experiments demonstrate that DVW improves the performance of popular value-based deep RL algorithms on a set of MinAtar benchmarks.

Learning Generative Models with Goal-conditioned Reinforcement Learning

We present a novel, alternative framework for learning generative models with goal-conditioned reinforcement learning. We define two agents, a goal conditioned agent (GC-agent) and a supervised agent (S-agent). Given a user-input initial state, the GC-agent learns to reconstruct the training set. In this context, elements in the training set are the goals. During training, the S-agent learns to imitate the GC-agent while remaining agnostic of the goals. At inference we generate new samples with the S-agent. Following a similar route as in variational auto-encoders, we derive an upper bound on the negative log-likelihood that consists of a reconstruction term and a divergence between the GC-agent policy and the (goal-agnostic) S-agent policy. We empirically demonstrate that our method is able to generate diverse and high quality samples in the task of image synthesis.

Adapting to game trees in zero-sum imperfect information games

Imperfect information games (IIG) are games in which each player only partially observes the current game state. We study how to learn $\epsilon$-optimal strategies in a zero-sum IIG through self-play with trajectory feedback. We give a problem-independent lower bound $\mathcal{O}(H(A_{\mathcal{X}}+B_{\mathcal{Y}})/\epsilon^2)$ on the required number of realizations to learn these strategies with high probability, where $H$ is the length of the game, $A_{\mathcal{X}}$ and $B_{\mathcal{Y}}$ are the total number of actions for the two players. We also propose two Follow the Regularize leader (FTRL) algorithms for this setting: Balanced-FTRL which matches this lower bound, but requires the knowledge of the information set structure beforehand to define the regularization; and Adaptive-FTRL which needs $\mathcal{O}(H^2(A_{\mathcal{X}}+B_{\mathcal{Y}})/\epsilon^2)$ plays without this requirement by progressively adapting the regularization to the observations.

KL-Entropy-Regularized RL with a Generative Model is Minimax Optimal

In this work, we consider and analyze the sample complexity of model-free reinforcement learning with a generative model. Particularly, we analyze mirror descent value iteration (MDVI) by Geist et al. (2019) and Vieillard et al. (2020a), which uses the Kullback-Leibler divergence and entropy regularization in its value and policy updates. Our analysis shows that it is nearly minimax-optimal for finding an $\varepsilon$-optimal policy when $\varepsilon$ is sufficiently small. This is the first theoretical result that demonstrates that a simple model-free algorithm without variance-reduction can be nearly minimax-optimal under the considered setting.

Indexed Minimum Empirical Divergence for Unimodal Bandits

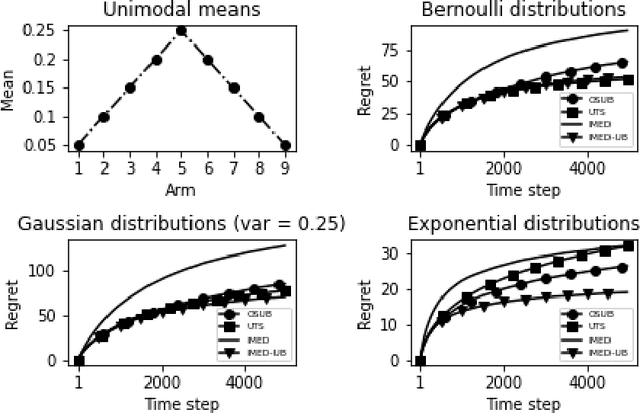
We consider a multi-armed bandit problem specified by a set of one-dimensional family exponential distributions endowed with a unimodal structure. We introduce IMED-UB, a algorithm that optimally exploits the unimodal-structure, by adapting to this setting the Indexed Minimum Empirical Divergence (IMED) algorithm introduced by Honda and Takemura [2015]. Owing to our proof technique, we are able to provide a concise finite-time analysis of IMED-UB algorithm. Numerical experiments show that IMED-UB competes with the state-of-the-art algorithms.

Adaptive Multi-Goal Exploration

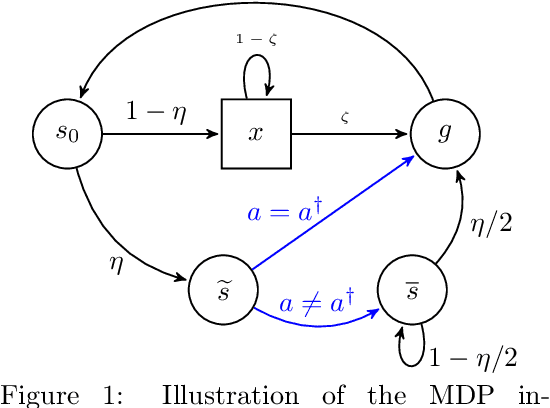
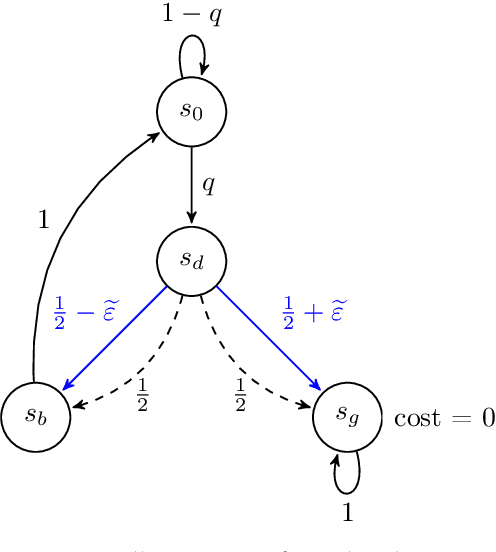
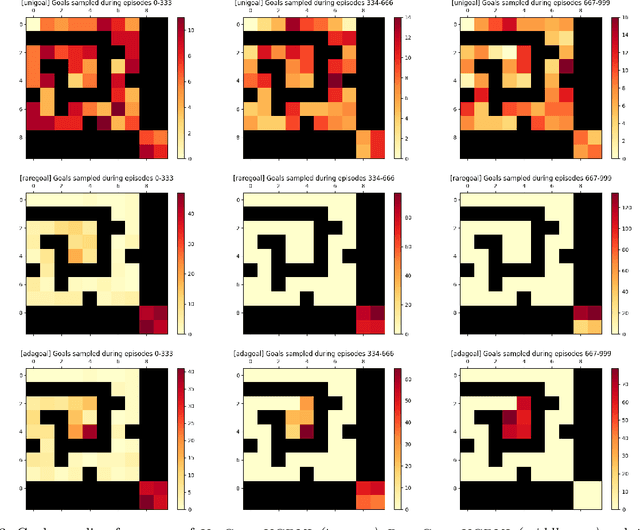
We introduce a generic strategy for provably efficient multi-goal exploration. It relies on AdaGoal, a novel goal selection scheme that is based on a simple constrained optimization problem, which adaptively targets goal states that are neither too difficult nor too easy to reach according to the agent's current knowledge. We show how AdaGoal can be used to tackle the objective of learning an $\epsilon$-optimal goal-conditioned policy for all the goal states that are reachable within $L$ steps in expectation from a reference state $s_0$ in a reward-free Markov decision process. In the tabular case with $S$ states and $A$ actions, our algorithm requires $\tilde{O}(L^3 S A \epsilon^{-2})$ exploration steps, which is nearly minimax optimal. We also readily instantiate AdaGoal in linear mixture Markov decision processes, which yields the first goal-oriented PAC guarantee with linear function approximation. Beyond its strong theoretical guarantees, AdaGoal is anchored in the high-level algorithmic structure of existing methods for goal-conditioned deep reinforcement learning.

Problem Dependent View on Structured Thresholding Bandit Problems

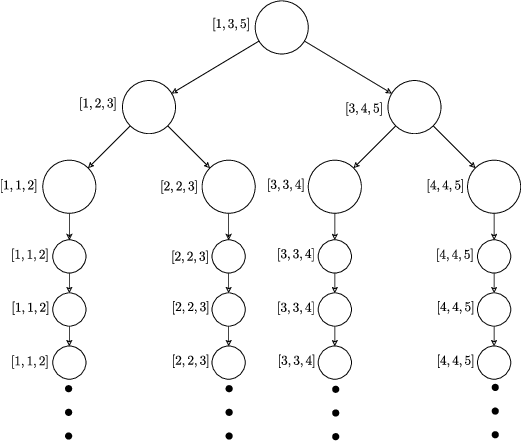
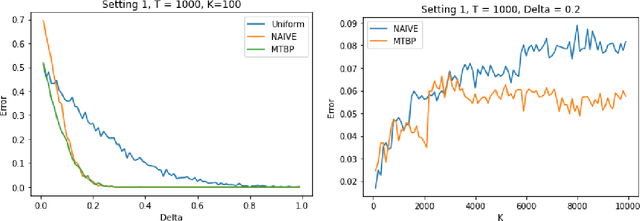
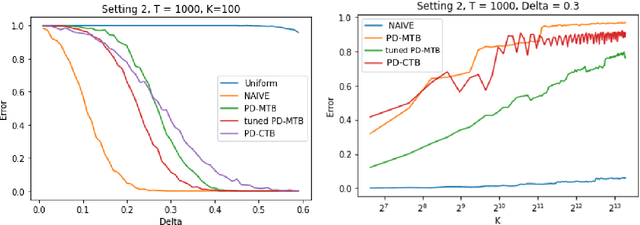
We investigate the problem dependent regime in the stochastic Thresholding Bandit problem (TBP) under several shape constraints. In the TBP, the objective of the learner is to output, at the end of a sequential game, the set of arms whose means are above a given threshold. The vanilla, unstructured, case is already well studied in the literature. Taking $K$ as the number of arms, we consider the case where (i) the sequence of arm's means $(\mu_k)_{k=1}^K$ is monotonically increasing (MTBP) and (ii) the case where $(\mu_k)_{k=1}^K$ is concave (CTBP). We consider both cases in the problem dependent regime and study the probability of error - i.e. the probability to mis-classify at least one arm. In the fixed budget setting, we provide upper and lower bounds for the probability of error in both the concave and monotone settings, as well as associated algorithms. In both settings the bounds match in the problem dependent regime up to universal constants in the exponential.

Model-Free Learning for Two-Player Zero-Sum Partially Observable Markov Games with Perfect Recall

We study the problem of learning a Nash equilibrium (NE) in an imperfect information game (IIG) through self-play. Precisely, we focus on two-player, zero-sum, episodic, tabular IIG under the perfect-recall assumption where the only feedback is realizations of the game (bandit feedback). In particular, the dynamic of the IIG is not known -- we can only access it by sampling or interacting with a game simulator. For this learning setting, we provide the Implicit Exploration Online Mirror Descent (IXOMD) algorithm. It is a model-free algorithm with a high-probability bound on the convergence rate to the NE of order $1/\sqrt{T}$ where $T$ is the number of played games. Moreover, IXOMD is computationally efficient as it needs to perform the updates only along the sampled trajectory.