James Cheshire
Problem Dependent View on Structured Thresholding Bandit Problems
Jun 18, 2021

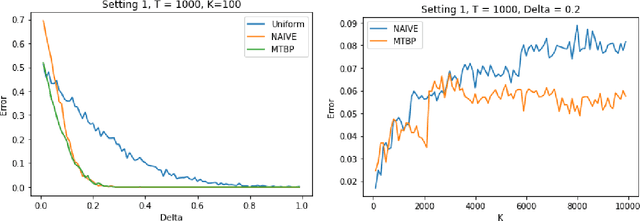
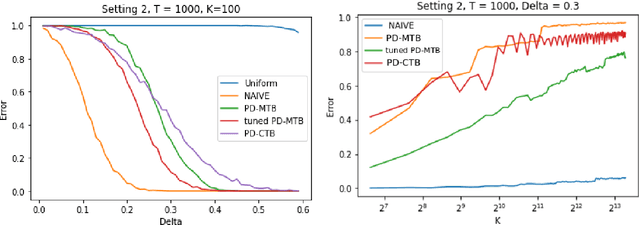
Abstract:We investigate the problem dependent regime in the stochastic Thresholding Bandit problem (TBP) under several shape constraints. In the TBP, the objective of the learner is to output, at the end of a sequential game, the set of arms whose means are above a given threshold. The vanilla, unstructured, case is already well studied in the literature. Taking $K$ as the number of arms, we consider the case where (i) the sequence of arm's means $(\mu_k)_{k=1}^K$ is monotonically increasing (MTBP) and (ii) the case where $(\mu_k)_{k=1}^K$ is concave (CTBP). We consider both cases in the problem dependent regime and study the probability of error - i.e. the probability to mis-classify at least one arm. In the fixed budget setting, we provide upper and lower bounds for the probability of error in both the concave and monotone settings, as well as associated algorithms. In both settings the bounds match in the problem dependent regime up to universal constants in the exponential.
Bandits with many optimal arms
Mar 23, 2021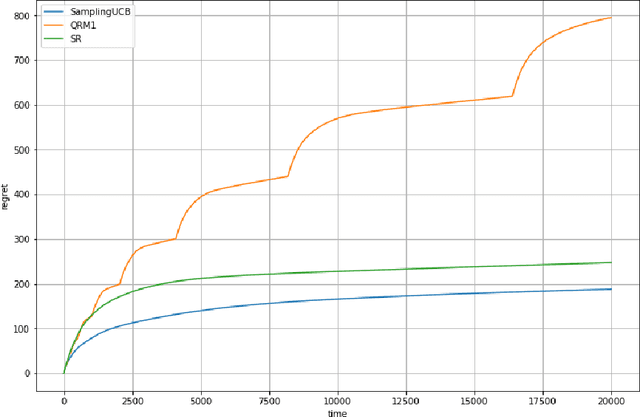
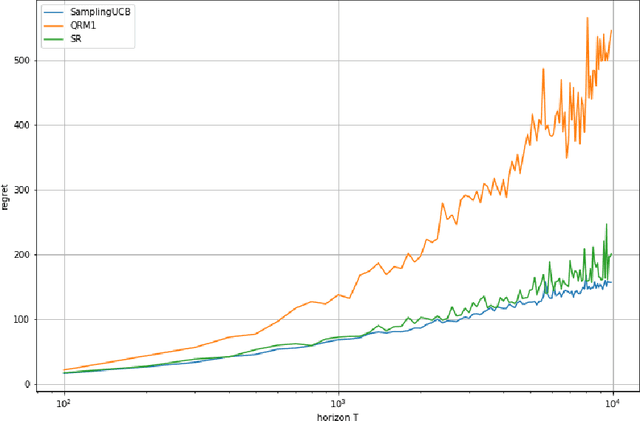
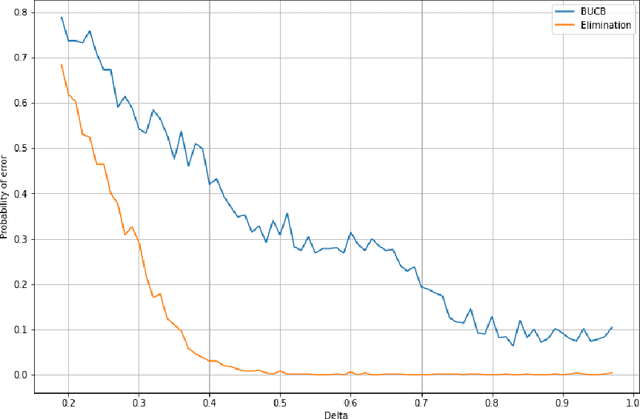
Abstract:We consider a stochastic bandit problem with a possibly infinite number of arms. We write $p^*$ for the proportion of optimal arms and $\Delta$ for the minimal mean-gap between optimal and sub-optimal arms. We characterize the optimal learning rates both in the cumulative regret setting, and in the best-arm identification setting in terms of the problem parameters $T$ (the budget), $p^*$ and $\Delta$. For the objective of minimizing the cumulative regret, we provide a lower bound of order $\Omega(\log(T)/(p^*\Delta))$ and a UCB-style algorithm with matching upper bound up to a factor of $\log(1/\Delta)$. Our algorithm needs $p^*$ to calibrate its parameters, and we prove that this knowledge is necessary, since adapting to $p^*$ in this setting is impossible. For best-arm identification we also provide a lower bound of order $\Omega(\exp(-cT\Delta^2p^*))$ on the probability of outputting a sub-optimal arm where $c>0$ is an absolute constant. We also provide an elimination algorithm with an upper bound matching the lower bound up to a factor of order $\log(1/\Delta)$ in the exponential, and that does not need $p^*$ or $\Delta$ as parameter.
The Influence of Shape Constraints on the Thresholding Bandit Problem
Jun 17, 2020


Abstract:We investigate the stochastic Thresholding Bandit problem (TBP) under several shape constraints. On top of (i) the vanilla, unstructured TBP, we consider the case where (ii) the sequence of arm's means $(\mu_k)_k$ is monotonically increasing MTBP, (iii) the case where $(\mu_k)_k$ is unimodal UTBP and (iv) the case where $(\mu_k)_k$ is concave CTBP. In the TBP problem the aim is to output, at the end of the sequential game, the set of arms whose means are above a given threshold. The regret is the highest gap between a misclassified arm and the threshold. In the fixed budget setting, we provide problem independent minimax rates for the expected regret in all settings, as well as associated algorithms. We prove that the minimax rates for the regret are (i) $\sqrt{\log(K)K/T}$ for TBP, (ii) $\sqrt{\log(K)/T}$ for MTBP, (iii) $\sqrt{K/T}$ for UTBP and (iv) $\sqrt{\log\log K/T}$ for CTBP, where $K$ is the number of arms and $T$ is the budget. These rates demonstrate that the dependence on $K$ of the minimax regret varies significantly depending on the shape constraint. This highlights the fact that the shape constraints modify fundamentally the nature of the TBP.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge