Problem Dependent View on Structured Thresholding Bandit Problems
Paper and Code
Jun 18, 2021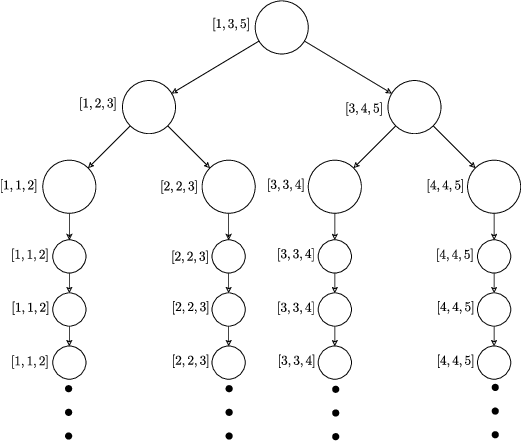

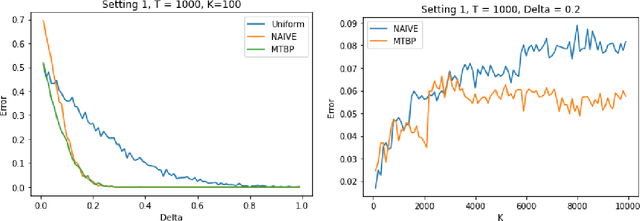
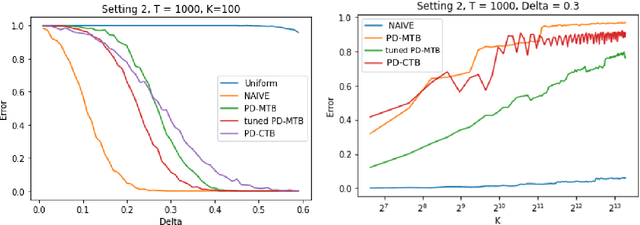
We investigate the problem dependent regime in the stochastic Thresholding Bandit problem (TBP) under several shape constraints. In the TBP, the objective of the learner is to output, at the end of a sequential game, the set of arms whose means are above a given threshold. The vanilla, unstructured, case is already well studied in the literature. Taking $K$ as the number of arms, we consider the case where (i) the sequence of arm's means $(\mu_k)_{k=1}^K$ is monotonically increasing (MTBP) and (ii) the case where $(\mu_k)_{k=1}^K$ is concave (CTBP). We consider both cases in the problem dependent regime and study the probability of error - i.e. the probability to mis-classify at least one arm. In the fixed budget setting, we provide upper and lower bounds for the probability of error in both the concave and monotone settings, as well as associated algorithms. In both settings the bounds match in the problem dependent regime up to universal constants in the exponential.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge