Indexed Minimum Empirical Divergence for Unimodal Bandits

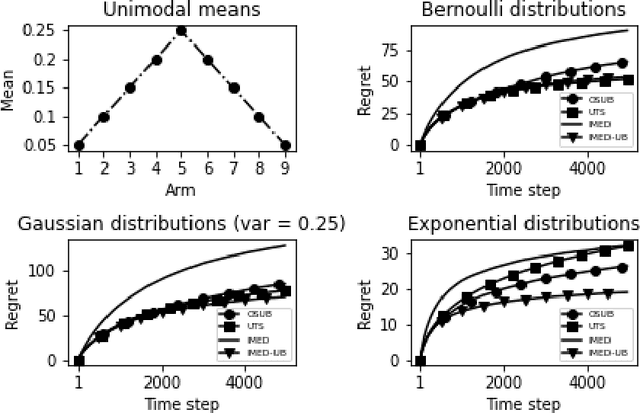
We consider a multi-armed bandit problem specified by a set of one-dimensional family exponential distributions endowed with a unimodal structure. We introduce IMED-UB, a algorithm that optimally exploits the unimodal-structure, by adapting to this setting the Indexed Minimum Empirical Divergence (IMED) algorithm introduced by Honda and Takemura [2015]. Owing to our proof technique, we are able to provide a concise finite-time analysis of IMED-UB algorithm. Numerical experiments show that IMED-UB competes with the state-of-the-art algorithms.

Optimal Strategies for Graph-Structured Bandits

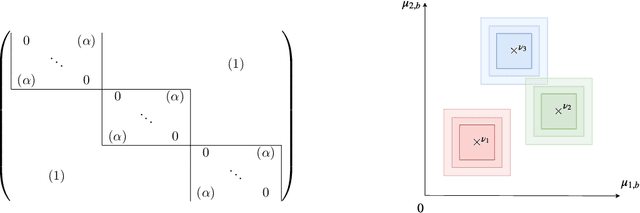
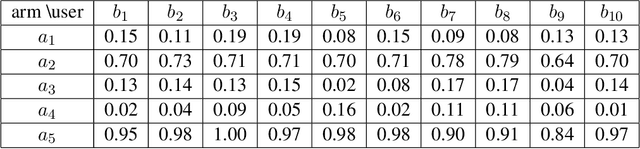
We study a structured variant of the multi-armed bandit problem specified by a set of Bernoulli distributions $ \nu \!= \!(\nu\_{a,b})\_{a \in \mathcal{A}, b \in \mathcal{B}}$ with means $(\mu\_{a,b})\_{a \in \mathcal{A}, b \in \mathcal{B}}\!\in\![0,1]^{\mathcal{A}\times\mathcal{B}}$ and by a given weight matrix $\omega\!=\! (\omega\_{b,b'})\_{b,b' \in \mathcal{B}}$, where $ \mathcal{A}$ is a finite set of arms and $ \mathcal{B} $ is a finite set of users. The weight matrix $\omega$ is such that for any two users $b,b'\!\in\!\mathcal{B}, \text{max}\_{a\in\mathcal{A}}|\mu\_{a,b} \!-\! \mu\_{a,b'}| \!\leq\! \omega\_{b,b'} $. This formulation is flexible enough to capture various situations, from highly-structured scenarios ($\omega\!\in\!\{0,1\}^{\mathcal{B}\times\mathcal{B}}$) to fully unstructured setups ($\omega\!\equiv\! 1$).We consider two scenarios depending on whether the learner chooses only the actions to sample rewards from or both users and actions. We first derive problem-dependent lower bounds on the regret for this generic graph-structure that involves a structure dependent linear programming problem. Second, we adapt to this setting the Indexed Minimum Empirical Divergence (IMED) algorithm introduced by Honda and Takemura (2015), and introduce the IMED-GS$^\star$ algorithm. Interestingly, IMED-GS$^\star$ does not require computing the solution of the linear programming problem more than about $\log(T)$ times after $T$ steps, while being provably asymptotically optimal. Also, unlike existing bandit strategies designed for other popular structures, IMED-GS$^\star$ does not resort to an explicit forced exploration scheme and only makes use of local counts of empirical events. We finally provide numerical illustration of our results that confirm the performance of IMED-GS$^\star$.

Forced-exploration free Strategies for Unimodal Bandits

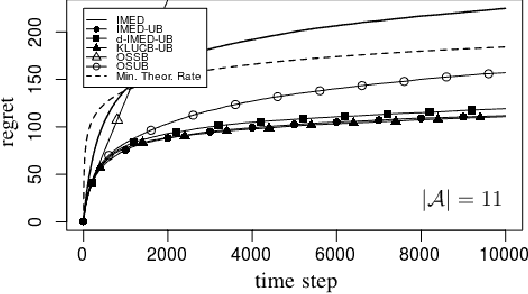
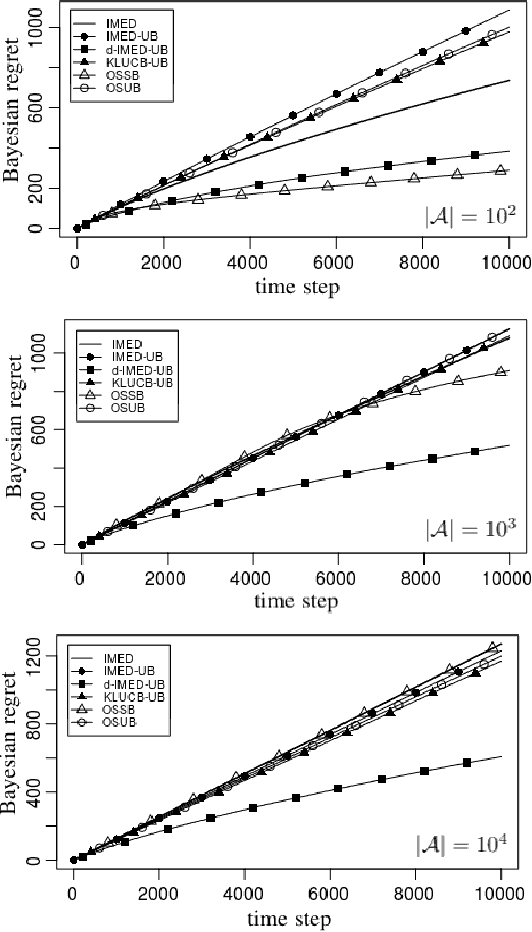
We consider a multi-armed bandit problem specified by a set of Gaussian or Bernoulli distributions endowed with a unimodal structure. Although this problem has been addressed in the literature (Combes and Proutiere, 2014), the state-of-the-art algorithms for such structure make appear a forced-exploration mechanism. We introduce IMED-UB, the first forced-exploration free strategy that exploits the unimodal-structure, by adapting to this setting the Indexed Minimum Empirical Divergence (IMED) strategy introduced by Honda and Takemura (2015). This strategy is proven optimal. We then derive KLUCB-UB, a KLUCB version of IMED-UB, which is also proven optimal. Owing to our proof technique, we are further able to provide a concise finite-time analysis of both strategies in an unified way. Numerical experiments show that both IMED-UB and KLUCB-UB perform similarly in practice and outperform the state-of-the-art algorithms.