Optimal Strategies for Graph-Structured Bandits
Paper and Code
Jul 10, 2020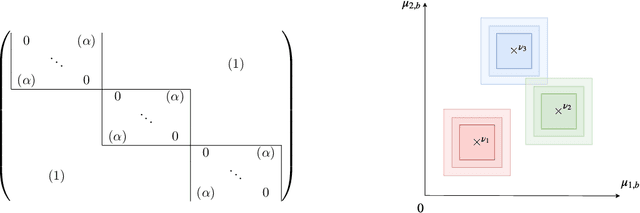
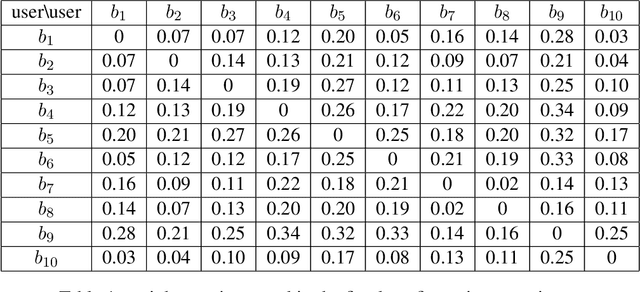
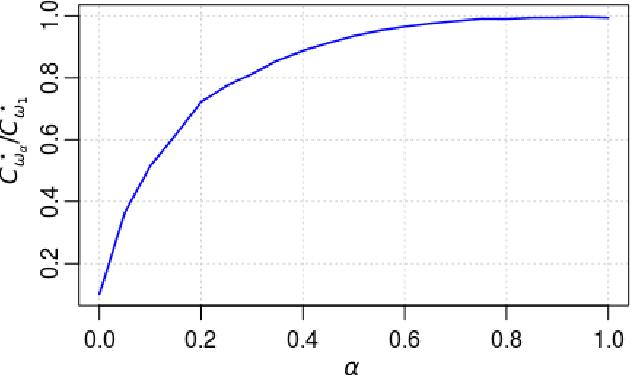
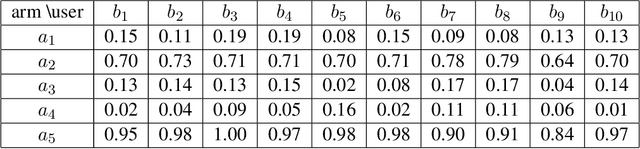
We study a structured variant of the multi-armed bandit problem specified by a set of Bernoulli distributions $ \nu \!= \!(\nu\_{a,b})\_{a \in \mathcal{A}, b \in \mathcal{B}}$ with means $(\mu\_{a,b})\_{a \in \mathcal{A}, b \in \mathcal{B}}\!\in\![0,1]^{\mathcal{A}\times\mathcal{B}}$ and by a given weight matrix $\omega\!=\! (\omega\_{b,b'})\_{b,b' \in \mathcal{B}}$, where $ \mathcal{A}$ is a finite set of arms and $ \mathcal{B} $ is a finite set of users. The weight matrix $\omega$ is such that for any two users $b,b'\!\in\!\mathcal{B}, \text{max}\_{a\in\mathcal{A}}|\mu\_{a,b} \!-\! \mu\_{a,b'}| \!\leq\! \omega\_{b,b'} $. This formulation is flexible enough to capture various situations, from highly-structured scenarios ($\omega\!\in\!\{0,1\}^{\mathcal{B}\times\mathcal{B}}$) to fully unstructured setups ($\omega\!\equiv\! 1$).We consider two scenarios depending on whether the learner chooses only the actions to sample rewards from or both users and actions. We first derive problem-dependent lower bounds on the regret for this generic graph-structure that involves a structure dependent linear programming problem. Second, we adapt to this setting the Indexed Minimum Empirical Divergence (IMED) algorithm introduced by Honda and Takemura (2015), and introduce the IMED-GS$^\star$ algorithm. Interestingly, IMED-GS$^\star$ does not require computing the solution of the linear programming problem more than about $\log(T)$ times after $T$ steps, while being provably asymptotically optimal. Also, unlike existing bandit strategies designed for other popular structures, IMED-GS$^\star$ does not resort to an explicit forced exploration scheme and only makes use of local counts of empirical events. We finally provide numerical illustration of our results that confirm the performance of IMED-GS$^\star$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge