Adaptive Multi-Goal Exploration
Paper and Code
Nov 23, 2021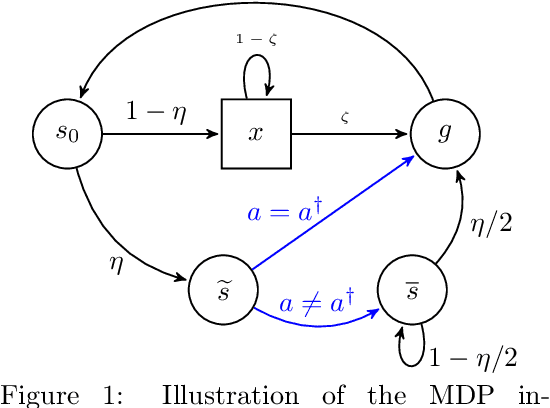
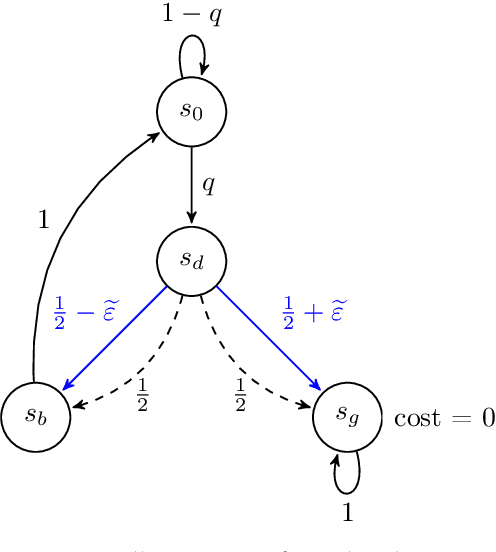
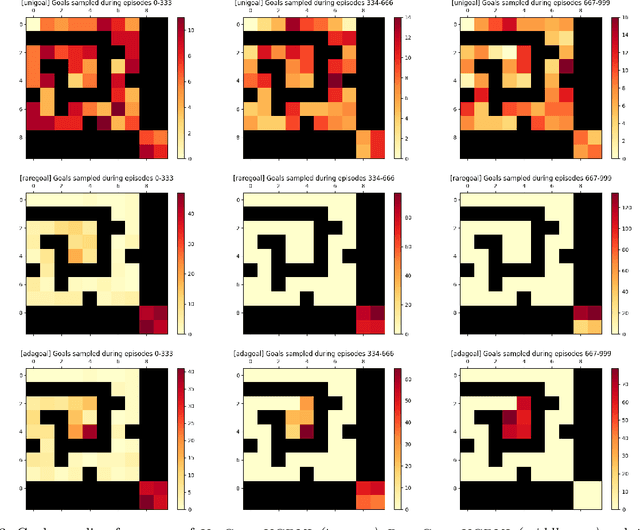
We introduce a generic strategy for provably efficient multi-goal exploration. It relies on AdaGoal, a novel goal selection scheme that is based on a simple constrained optimization problem, which adaptively targets goal states that are neither too difficult nor too easy to reach according to the agent's current knowledge. We show how AdaGoal can be used to tackle the objective of learning an $\epsilon$-optimal goal-conditioned policy for all the goal states that are reachable within $L$ steps in expectation from a reference state $s_0$ in a reward-free Markov decision process. In the tabular case with $S$ states and $A$ actions, our algorithm requires $\tilde{O}(L^3 S A \epsilon^{-2})$ exploration steps, which is nearly minimax optimal. We also readily instantiate AdaGoal in linear mixture Markov decision processes, which yields the first goal-oriented PAC guarantee with linear function approximation. Beyond its strong theoretical guarantees, AdaGoal is anchored in the high-level algorithmic structure of existing methods for goal-conditioned deep reinforcement learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge