On-the-Fly VLA Adaptation via Test-Time Reinforcement Learning

Vision-Language-Action models have recently emerged as a powerful paradigm for general-purpose robot learning, enabling agents to map visual observations and natural-language instructions into executable robotic actions. Though popular, they are primarily trained via supervised fine-tuning or training-time reinforcement learning, requiring explicit fine-tuning phases, human interventions, or controlled data collection. Consequently, existing methods remain unsuitable for challenging simulated- or physical-world deployments, where robots must respond autonomously and flexibly to evolving environments. To address this limitation, we introduce a Test-Time Reinforcement Learning for VLAs (TT-VLA), a framework that enables on-the-fly policy adaptation during inference. TT-VLA formulates a dense reward mechanism that leverages step-by-step task-progress signals to refine action policies during test time while preserving the SFT/RL-trained priors, making it an effective supplement to current VLA models. Empirical results show that our approach enhances overall adaptability, stability, and task success in dynamic, previously unseen scenarios under simulated and real-world settings. We believe TT-VLA offers a principled step toward self-improving, deployment-ready VLAs.

Deep But Reliable: Advancing Multi-turn Reasoning for Thinking with Images

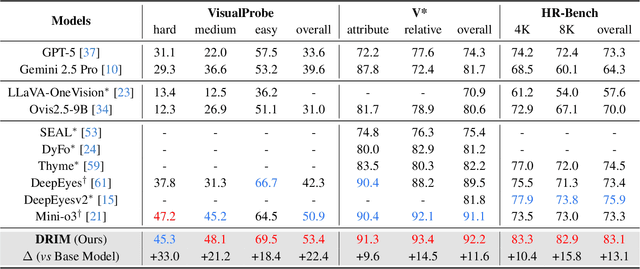
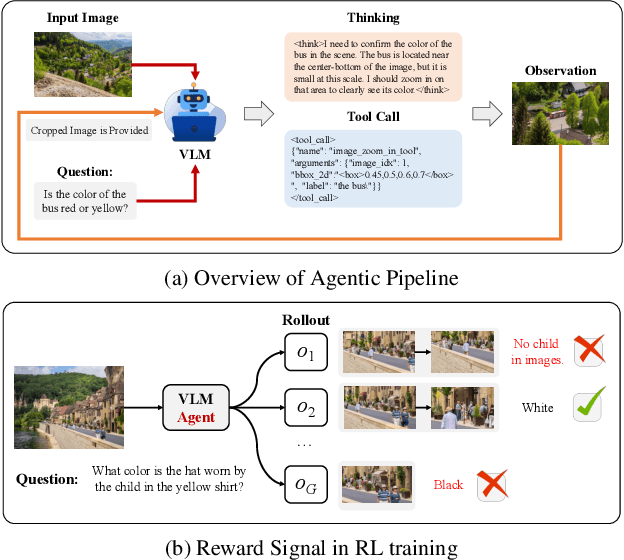
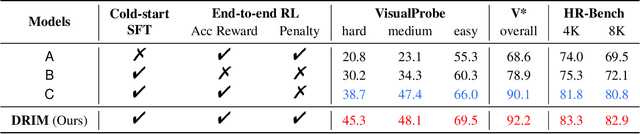
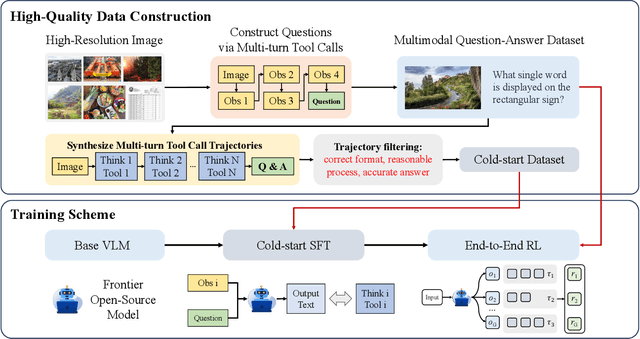
Recent advances in large Vision-Language Models (VLMs) have exhibited strong reasoning capabilities on complex visual tasks by thinking with images in their Chain-of-Thought (CoT), which is achieved by actively invoking tools to analyze visual inputs rather than merely perceiving them. However, existing models often struggle to reflect on and correct themselves when attempting incorrect reasoning trajectories. To address this limitation, we propose DRIM, a model that enables deep but reliable multi-turn reasoning when thinking with images in its multimodal CoT. Our pipeline comprises three stages: data construction, cold-start SFT and RL. Based on a high-resolution image dataset, we construct high-difficulty and verifiable visual question-answer pairs, where solving each task requires multi-turn tool calls to reach the correct answer. In the SFT stage, we collect tool trajectories as cold-start data, guiding a multi-turn reasoning pattern. In the RL stage, we introduce redundancy-penalized policy optimization, which incentivizes the model to develop a self-reflective reasoning pattern. The basic idea is to impose judgment on reasoning trajectories and penalize those that produce incorrect answers without sufficient multi-scale exploration. Extensive experiments demonstrate that DRIM achieves superior performance on visual understanding benchmarks.

Listening for "You": Enhancing Speech Image Retrieval via Target Speaker Extraction

Image retrieval using spoken language cues has emerged as a promising direction in multimodal perception, yet leveraging speech in multi-speaker scenarios remains challenging. We propose a novel Target Speaker Speech-Image Retrieval task and a framework that learns the relationship between images and multi-speaker speech signals in the presence of a target speaker. Our method integrates pre-trained self-supervised audio encoders with vision models via target speaker-aware contrastive learning, conditioned on a Target Speaker Extraction and Retrieval module. This enables the system to extract spoken commands from the target speaker and align them with corresponding images. Experiments on SpokenCOCO2Mix and SpokenCOCO3Mix show that TSRE significantly outperforms existing methods, achieving 36.3% and 29.9% Recall@1 in 2 and 3 speaker scenarios, respectively - substantial improvements over single speaker baselines and state-of-the-art models. Our approach demonstrates potential for real-world deployment in assistive robotics and multimodal interaction systems.

Improved Analysis for Sign-based Methods with Momentum Updates

In this paper, we present enhanced analysis for sign-based optimization algorithms with momentum updates. Traditional sign-based methods, under the separable smoothness assumption, guarantee a convergence rate of $\mathcal{O}(T^{-1/4})$, but they either require large batch sizes or assume unimodal symmetric stochastic noise. To address these limitations, we demonstrate that signSGD with momentum can achieve the same convergence rate using constant batch sizes without additional assumptions. Our analysis, under the standard $l_2$-smoothness condition, improves upon the result of the prior momentum-based signSGD method by a factor of $\mathcal{O}(d^{1/2})$, where $d$ is the problem dimension. Furthermore, we explore sign-based methods with majority vote in distributed settings and show that the proposed momentum-based method yields convergence rates of $\mathcal{O}\left( d^{1/2}T^{-1/2} + dn^{-1/2} \right)$ and $\mathcal{O}\left( \max \{ d^{1/4}T^{-1/4}, d^{1/10}T^{-1/5} \} \right)$, which outperform the previous results of $\mathcal{O}\left( dT^{-1/4} + dn^{-1/2} \right)$ and $\mathcal{O}\left( d^{3/8}T^{-1/8} \right)$, respectively. Numerical experiments further validate the effectiveness of the proposed methods.

Discounted Online Convex Optimization: Uniform Regret Across a Continuous Interval

Reflecting the greater significance of recent history over the distant past in non-stationary environments, $\lambda$-discounted regret has been introduced in online convex optimization (OCO) to gracefully forget past data as new information arrives. When the discount factor $\lambda$ is given, online gradient descent with an appropriate step size achieves an $O(1/\sqrt{1-\lambda})$ discounted regret. However, the value of $\lambda$ is often not predetermined in real-world scenarios. This gives rise to a significant open question: is it possible to develop a discounted algorithm that adapts to an unknown discount factor. In this paper, we affirmatively answer this question by providing a novel analysis to demonstrate that smoothed OGD (SOGD) achieves a uniform $O(\sqrt{\log T/1-\lambda})$ discounted regret, holding for all values of $\lambda$ across a continuous interval simultaneously. The basic idea is to maintain multiple OGD instances to handle different discount factors, and aggregate their outputs sequentially by an online prediction algorithm named as Discounted-Normal-Predictor (DNP) (Kapralov and Panigrahy,2010). Our analysis reveals that DNP can combine the decisions of two experts, even when they operate on discounted regret with different discount factors.

Cream of the Crop: Harvesting Rich, Scalable and Transferable Multi-Modal Data for Instruction Fine-Tuning

The hypothesis that pretrained large language models (LLMs) necessitate only minimal supervision during the fine-tuning (SFT) stage (Zhou et al., 2024) has been substantiated by recent advancements in data curation and selection research. However, their stability and generalizability are compromised due to the vulnerability to experimental setups and validation protocols, falling short of surpassing random sampling (Diddee & Ippolito, 2024; Xia et al., 2024b). Built upon LLMs, multi-modal LLMs (MLLMs), combined with the sheer token volume and heightened heterogeneity of data sources, amplify both the significance and complexity of data selection. To harvest multi-modal instructional data in a robust and efficient manner, we re-define the granularity of the quality metric by decomposing it into 14 vision-language-related capabilities, and introduce multi-modal rich scorers to evaluate the capabilities of each data candidate. To promote diversity, in light of the inherent objective of the alignment stage, we take interaction style as diversity indicator and use a multi-modal rich styler to identify data instruction patterns. In doing so, our multi-modal rich scorers and styler (mmSSR) guarantee that high-scoring information is conveyed to users in diversified forms. Free from embedding-based clustering or greedy sampling, mmSSR efficiently scales to millions of data with varying budget constraints, supports customization for general or specific capability acquisition, and facilitates training-free generalization to new domains for curation. Across 10+ experimental settings, validated by 14 multi-modal benchmarks, we demonstrate consistent improvements over random sampling, baseline strategies and state-of-the-art selection methods, achieving 99.1% of full performance with only 30% of the 2.6M data.

Exploring the Adversarial Vulnerabilities of Vision-Language-Action Models in Robotics

Recently in robotics, Vision-Language-Action (VLA) models have emerged as a transformative approach, enabling robots to execute complex tasks by integrating visual and linguistic inputs within an end-to-end learning framework. While VLA models offer significant capabilities, they also introduce new attack surfaces, making them vulnerable to adversarial attacks. With these vulnerabilities largely unexplored, this paper systematically quantifies the robustness of VLA-based robotic systems. Recognizing the unique demands of robotic execution, our attack objectives target the inherent spatial and functional characteristics of robotic systems. In particular, we introduce an untargeted position-aware attack objective that leverages spatial foundations to destabilize robotic actions, and a targeted attack objective that manipulates the robotic trajectory. Additionally, we design an adversarial patch generation approach that places a small, colorful patch within the camera's view, effectively executing the attack in both digital and physical environments. Our evaluation reveals a marked degradation in task success rates, with up to a 100\% reduction across a suite of simulated robotic tasks, highlighting critical security gaps in current VLA architectures. By unveiling these vulnerabilities and proposing actionable evaluation metrics, this work advances both the understanding and enhancement of safety for VLA-based robotic systems, underscoring the necessity for developing robust defense strategies prior to physical-world deployments.

Limit Theorems for Stochastic Gradient Descent with Infinite Variance

Stochastic gradient descent is a classic algorithm that has gained great popularity especially in the last decades as the most common approach for training models in machine learning. While the algorithm has been well-studied when stochastic gradients are assumed to have a finite variance, there is significantly less research addressing its theoretical properties in the case of infinite variance gradients. In this paper, we establish the asymptotic behavior of stochastic gradient descent in the context of infinite variance stochastic gradients, assuming that the stochastic gradient is regular varying with index $\alpha\in(1,2)$. The closest result in this context was established in 1969 , in the one-dimensional case and assuming that stochastic gradients belong to a more restrictive class of distributions. We extend it to the multidimensional case, covering a broader class of infinite variance distributions. As we show, the asymptotic distribution of the stochastic gradient descent algorithm can be characterized as the stationary distribution of a suitably defined Ornstein-Uhlenbeck process driven by an appropriate stable L\'evy process. Additionally, we explore the applications of these results in linear regression and logistic regression models.

Neuron-based Personality Trait Induction in Large Language Models

Large language models (LLMs) have become increasingly proficient at simulating various personality traits, an important capability for supporting related applications (e.g., role-playing). To further improve this capacity, in this paper, we present a neuron-based approach for personality trait induction in LLMs, with three major technical contributions. First, we construct PersonalityBench, a large-scale dataset for identifying and evaluating personality traits in LLMs. This dataset is grounded in the Big Five personality traits from psychology and is designed to assess the generative capabilities of LLMs towards specific personality traits. Second, by leveraging PersonalityBench, we propose an efficient method for identifying personality-related neurons within LLMs by examining the opposite aspects of a given trait. Third, we develop a simple yet effective induction method that manipulates the values of these identified personality-related neurons. This method enables fine-grained control over the traits exhibited by LLMs without training and modifying model parameters. Extensive experiments validate the efficacy of our neuron identification and trait induction methods. Notably, our approach achieves comparable performance as fine-tuned models, offering a more efficient and flexible solution for personality trait induction in LLMs. We provide access to all the mentioned resources at https://github.com/RUCAIBox/NPTI.

You Only Speak Once to See

Grounding objects in images using visual cues is a well-established approach in computer vision, yet the potential of audio as a modality for object recognition and grounding remains underexplored. We introduce YOSS, "You Only Speak Once to See," to leverage audio for grounding objects in visual scenes, termed Audio Grounding. By integrating pre-trained audio models with visual models using contrastive learning and multi-modal alignment, our approach captures speech commands or descriptions and maps them directly to corresponding objects within images. Experimental results indicate that audio guidance can be effectively applied to object grounding, suggesting that incorporating audio guidance may enhance the precision and robustness of current object grounding methods and improve the performance of robotic systems and computer vision applications. This finding opens new possibilities for advanced object recognition, scene understanding, and the development of more intuitive and capable robotic systems.