Distributionally Robust Optimization as a Scalable Framework to Characterize Extreme Value Distributions

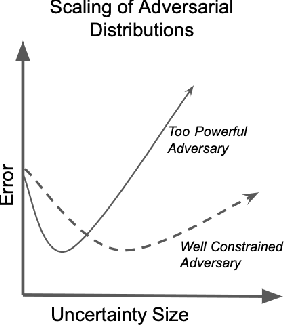
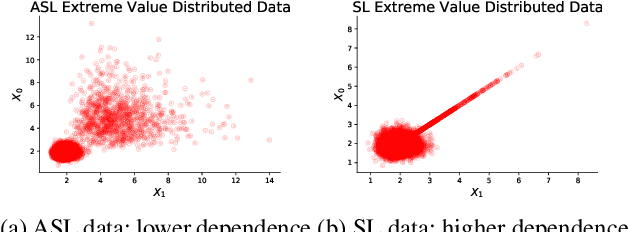
The goal of this paper is to develop distributionally robust optimization (DRO) estimators, specifically for multidimensional Extreme Value Theory (EVT) statistics. EVT supports using semi-parametric models called max-stable distributions built from spatial Poisson point processes. While powerful, these models are only asymptotically valid for large samples. However, since extreme data is by definition scarce, the potential for model misspecification error is inherent to these applications, thus DRO estimators are natural. In order to mitigate over-conservative estimates while enhancing out-of-sample performance, we study DRO estimators informed by semi-parametric max-stable constraints in the space of point processes. We study both tractable convex formulations for some problems of interest (e.g. CVaR) and more general neural network based estimators. Both approaches are validated using synthetically generated data, recovering prescribed characteristics, and verifying the efficacy of the proposed techniques. Additionally, the proposed method is applied to a real data set of financial returns for comparison to a previous analysis. We established the proposed model as a novel formulation in the multivariate EVT domain, and innovative with respect to performance when compared to relevant alternate proposals.

Robust Quickest Change Detection in Non-Stationary Processes

Optimal algorithms are developed for robust detection of changes in non-stationary processes. These are processes in which the distribution of the data after change varies with time. The decision-maker does not have access to precise information on the post-change distribution. It is shown that if the post-change non-stationary family has a distribution that is least favorable in a well-defined sense, then the algorithms designed using the least favorable distributions are robust and optimal. Non-stationary processes are encountered in public health monitoring and space and military applications. The robust algorithms are applied to real and simulated data to show their effectiveness.

Kidney Exchange with Inhomogeneous Edge Existence Uncertainty

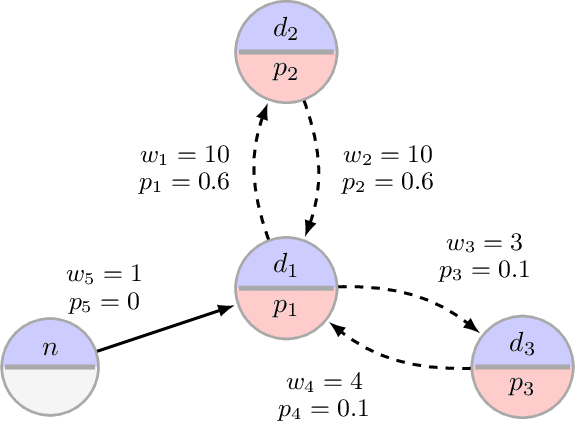
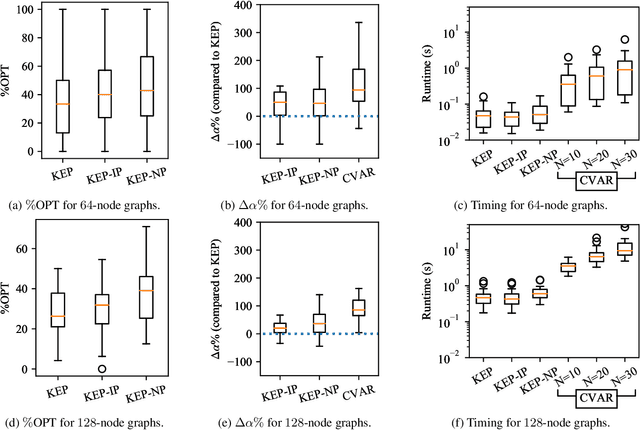
Motivated by kidney exchange, we study a stochastic cycle and chain packing problem, where we aim to identify structures in a directed graph to maximize the expectation of matched edge weights. All edges are subject to failure, and the failures can have nonidentical probabilities. To the best of our knowledge, the state-of-the-art approaches are only tractable when failure probabilities are identical. We formulate a relevant non-convex optimization problem and propose a tractable mixed-integer linear programming reformulation to solve it. In addition, we propose a model that integrates both risks and the expected utilities of the matching by incorporating conditional value at risk (CVaR) into the objective function, providing a robust formulation for this problem. Subsequently, we propose a sample-average-approximation (SAA) based approach to solve this problem. We test our approaches on data from the United Network for Organ Sharing (UNOS) and compare against state-of-the-art approaches. Our model provides better performance with the same running time as a leading deterministic approach (PICEF). Our CVaR extensions with an SAA-based method improves the $\alpha \times 100\%$ ($0<\alpha\leqslant 1$) worst-case performance substantially compared to existing models.

Optimizing vaccine distribution networks in low and middle-income countries

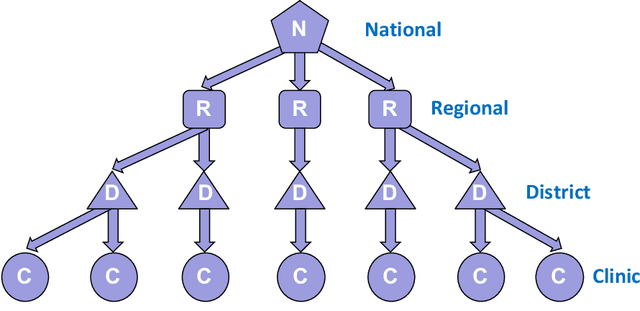
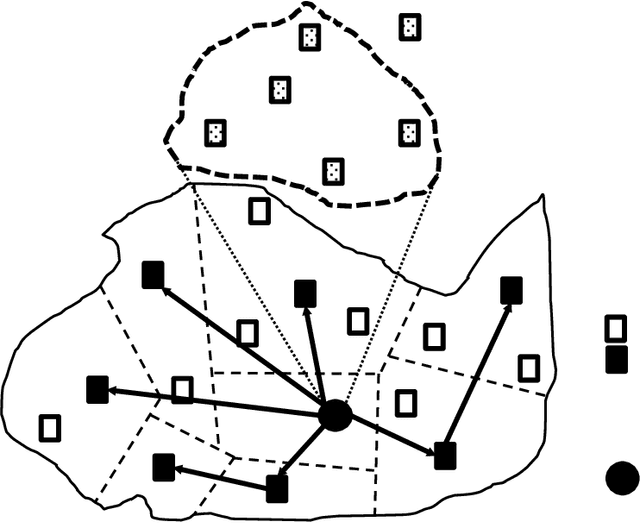
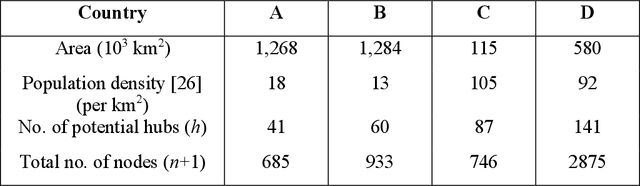
Vaccination has been proven to be the most effective method to prevent infectious diseases. However, there are still millions of children in low and middle-income countries who are not covered by routine vaccines and remain at risk. The World Health Organization's Expanded Programme on Immunization (WHO-EPI) was designed to provide universal childhood vaccine access for children across the world and in this work, we address the design of the distribution network for WHO-EPI vaccines. In particular, we formulate the network design problem as a mixed integer program (MIP) and present a new algorithm for typical problems that are too large to be solved using commercial MIP software. We test the algorithm using data derived from four different countries in sub-Saharan Africa and show that the algorithm is able to obtain high-quality solutions for even the largest problems within a few minutes.

Scalable Robust Kidney Exchange

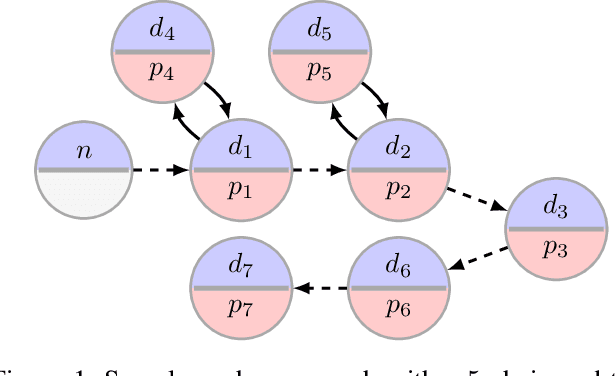
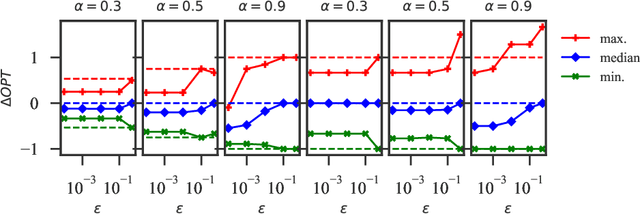
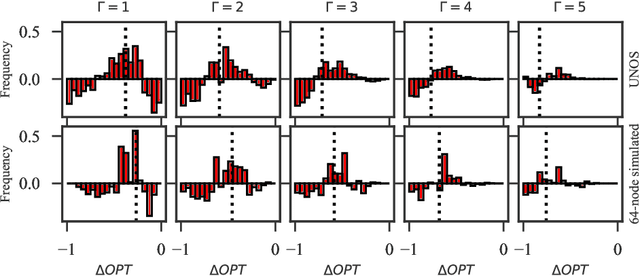
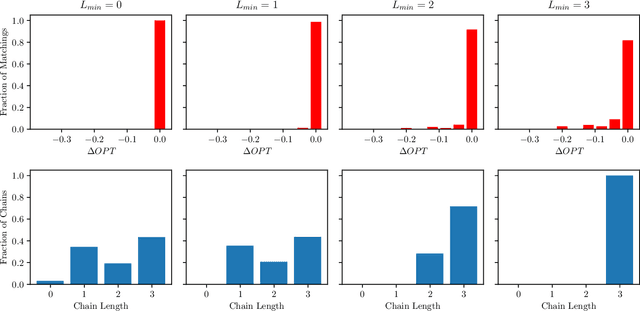
In barter exchanges, participants directly trade their endowed goods in a constrained economic setting without money. Transactions in barter exchanges are often facilitated via a central clearinghouse that must match participants even in the face of uncertainty---over participants, existence and quality of potential trades, and so on. Leveraging robust combinatorial optimization techniques, we address uncertainty in kidney exchange, a real-world barter market where patients swap (in)compatible paired donors. We provide two scalable robust methods to handle two distinct types of uncertainty in kidney exchange---over the quality and the existence of a potential match. The latter case directly addresses a weakness in all stochastic-optimization-based methods to the kidney exchange clearing problem, which all necessarily require explicit estimates of the probability of a transaction existing---a still-unsolved problem in this nascent market. We also propose a novel, scalable kidney exchange formulation that eliminates the need for an exponential-time constraint generation process in competing formulations, maintains provable optimality, and serves as a subsolver for our robust approach. For each type of uncertainty we demonstrate the benefits of robustness on real data from a large, fielded kidney exchange in the United States. We conclude by drawing parallels between robustness and notions of fairness in the kidney exchange setting.