Kidney Exchange with Inhomogeneous Edge Existence Uncertainty
Paper and Code
Jul 07, 2020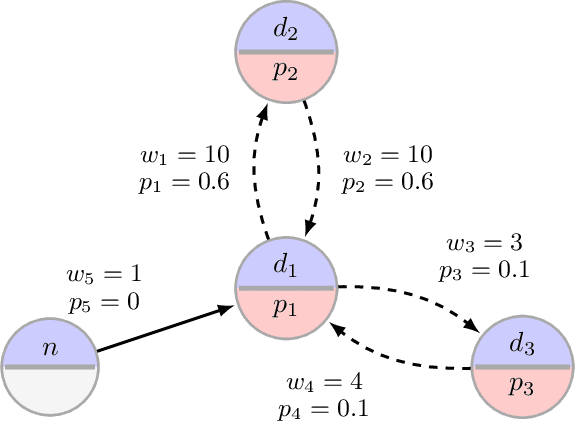

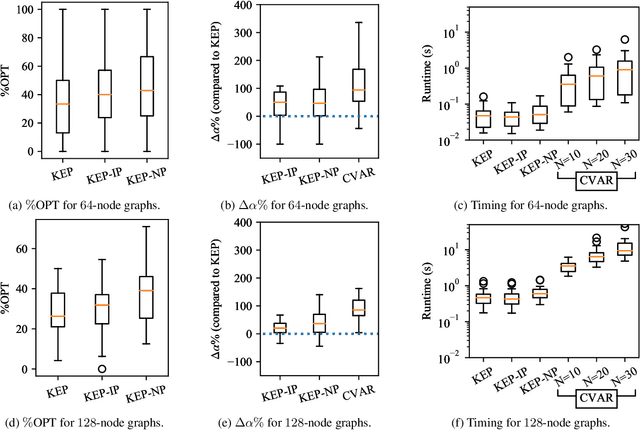
Motivated by kidney exchange, we study a stochastic cycle and chain packing problem, where we aim to identify structures in a directed graph to maximize the expectation of matched edge weights. All edges are subject to failure, and the failures can have nonidentical probabilities. To the best of our knowledge, the state-of-the-art approaches are only tractable when failure probabilities are identical. We formulate a relevant non-convex optimization problem and propose a tractable mixed-integer linear programming reformulation to solve it. In addition, we propose a model that integrates both risks and the expected utilities of the matching by incorporating conditional value at risk (CVaR) into the objective function, providing a robust formulation for this problem. Subsequently, we propose a sample-average-approximation (SAA) based approach to solve this problem. We test our approaches on data from the United Network for Organ Sharing (UNOS) and compare against state-of-the-art approaches. Our model provides better performance with the same running time as a leading deterministic approach (PICEF). Our CVaR extensions with an SAA-based method improves the $\alpha \times 100\%$ ($0<\alpha\leqslant 1$) worst-case performance substantially compared to existing models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge