Central Limit Theorem for ergodic averages of Markov chains \& the comparison of sampling algorithms for heavy-tailed distributions

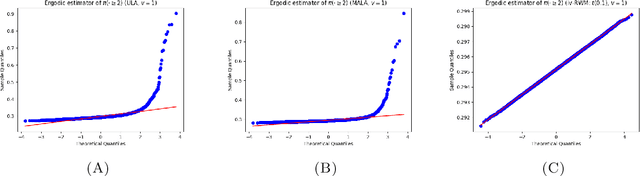
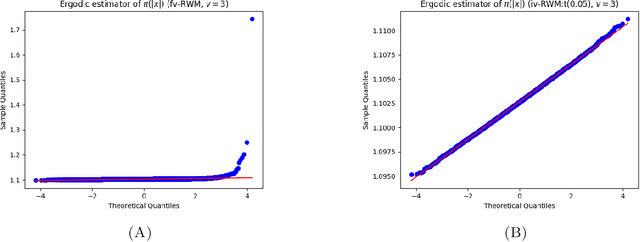
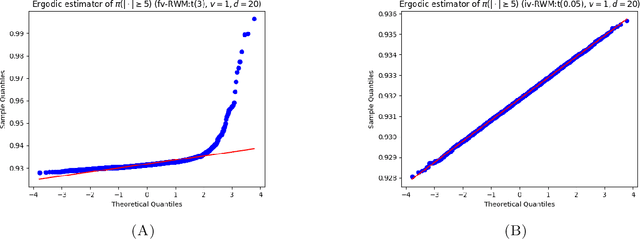
Establishing central limit theorems (CLTs) for ergodic averages of Markov chains is a fundamental problem in probability and its applications. Since the seminal work~\cite{MR834478}, a vast literature has emerged on the sufficient conditions for such CLTs. To counterbalance this, the present paper provides verifiable necessary conditions for CLTs of ergodic averages of Markov chains on general state spaces. Our theory is based on drift conditions, which also yield lower bounds on the rates of convergence to stationarity in various metrics. The validity of the ergodic CLT is of particular importance for sampling algorithms, where it underpins the error analysis of estimators in Bayesian statistics and machine learning. Although heavy-tailed sampling is of central importance in applications, the characterisation of the CLT and the convergence rates are theoretically poorly understood for almost all practically-used Markov chain Monte Carlo (MCMC) algorithms. In this setting our results provide sharp conditions on the validity of the ergodic CLT and establish convergence rates for large families of MCMC sampling algorithms for heavy-tailed targets. Our study includes a rather complete analyses for random walk Metropolis samplers (with finite- and infinite-variance proposals), Metropolis-adjusted and unadjusted Langevin algorithms and the stereographic projection sampler (as well as the independence sampler). By providing these sharp results via our practical drift conditions, our theory offers significant insights into the problems of algorithm selection and comparison for sampling heavy-tailed distributions (see short YouTube presentations~\cite{YouTube_talk} describing our \href{https://youtu.be/m2y7U4cEqy4}{\underline{theory}} and \href{https://youtu.be/w8I_oOweuko}{\underline{applications}}).

Limit Theorems for Stochastic Gradient Descent with Infinite Variance

Stochastic gradient descent is a classic algorithm that has gained great popularity especially in the last decades as the most common approach for training models in machine learning. While the algorithm has been well-studied when stochastic gradients are assumed to have a finite variance, there is significantly less research addressing its theoretical properties in the case of infinite variance gradients. In this paper, we establish the asymptotic behavior of stochastic gradient descent in the context of infinite variance stochastic gradients, assuming that the stochastic gradient is regular varying with index $\alpha\in(1,2)$. The closest result in this context was established in 1969 , in the one-dimensional case and assuming that stochastic gradients belong to a more restrictive class of distributions. We extend it to the multidimensional case, covering a broader class of infinite variance distributions. As we show, the asymptotic distribution of the stochastic gradient descent algorithm can be characterized as the stationary distribution of a suitably defined Ornstein-Uhlenbeck process driven by an appropriate stable L\'evy process. Additionally, we explore the applications of these results in linear regression and logistic regression models.

Non-asymptotic bounds for forward processes in denoising diffusions: Ornstein-Uhlenbeck is hard to beat

Denoising diffusion probabilistic models (DDPMs) represent a recent advance in generative modelling that has delivered state-of-the-art results across many domains of applications. Despite their success, a rigorous theoretical understanding of the error within DDPMs, particularly the non-asymptotic bounds required for the comparison of their efficiency, remain scarce. Making minimal assumptions on the initial data distribution, allowing for example the manifold hypothesis, this paper presents explicit non-asymptotic bounds on the forward diffusion error in total variation (TV), expressed as a function of the terminal time $T$. We parametrise multi-modal data distributions in terms of the distance $R$ to their furthest modes and consider forward diffusions with additive and multiplicative noise. Our analysis rigorously proves that, under mild assumptions, the canonical choice of the Ornstein-Uhlenbeck (OU) process cannot be significantly improved in terms of reducing the terminal time $T$ as a function of $R$ and error tolerance $\varepsilon>0$. Motivated by data distributions arising in generative modelling, we also establish a cut-off like phenomenon (as $R\to\infty$) for the convergence to its invariant measure in TV of an OU process, initialized at a multi-modal distribution with maximal mode distance $R$.

Non-asymptotic bounds for sampling algorithms without log-concavity

Discrete time analogues of ergodic stochastic differential equations (SDEs) are one of the most popular and flexible tools for sampling high-dimensional probability measures. Non-asymptotic analysis in the $L^2$ Wasserstein distance of sampling algorithms based on Euler discretisations of SDEs has been recently developed by several authors for log-concave probability distributions. In this work we replace the log-concavity assumption with a log-concavity at infinity condition. We provide novel $L^2$ convergence rates for Euler schemes, expressed explicitly in terms of problem parameters. From there we derive non-asymptotic bounds on the distance between the laws induced by Euler schemes and the invariant laws of SDEs, both for schemes with standard and with randomised (inaccurate) drifts. We also obtain bounds for the hierarchy of discretisation, which enables us to deploy a multi-level Monte Carlo estimator. Our proof relies on a novel construction of a coupling for the Markov chains that can be used to control both the $L^1$ and $L^2$ Wasserstein distances simultaneously. Finally, we provide a weak convergence analysis that covers both the standard and the randomised (inaccurate) drift case. In particular, we reveal that the variance of the randomised drift does not influence the rate of weak convergence of the Euler scheme to the SDE.