Non-convex entropic mean-field optimization via Best Response flow

We study the problem of minimizing non-convex functionals on the space of probability measures, regularized by the relative entropy (KL divergence) with respect to a fixed reference measure, as well as the corresponding problem of solving entropy-regularized non-convex-non-concave min-max problems. We utilize the Best Response flow (also known in the literature as the fictitious play flow) and study how its convergence is influenced by the relation between the degree of non-convexity of the functional under consideration, the regularization parameter and the tail behaviour of the reference measure. In particular, we demonstrate how to choose the regularizer, given the non-convex functional, so that the Best Response operator becomes a contraction with respect to the $L^1$-Wasserstein distance, which then ensures the existence of its unique fixed point, which is then shown to be the unique global minimizer for our optimization problem. This extends recent results where the Best Response flow was applied to solve convex optimization problems regularized by the relative entropy with respect to arbitrary reference measures, and with arbitrary values of the regularization parameter. Our results explain precisely how the assumption of convexity can be relaxed, at the expense of making a specific choice of the regularizer. Additionally, we demonstrate how these results can be applied in reinforcement learning in the context of policy optimization for Markov Decision Processes and Markov games with softmax parametrized policies in the mean-field regime.

Linear convergence of proximal descent schemes on the Wasserstein space

We investigate proximal descent methods, inspired by the minimizing movement scheme introduced by Jordan, Kinderlehrer and Otto, for optimizing entropy-regularized functionals on the Wasserstein space. We establish linear convergence under flat convexity assumptions, thereby relaxing the common reliance on geodesic convexity. Our analysis circumvents the need for discrete-time adaptations of the Evolution Variational Inequality (EVI). Instead, we leverage a uniform logarithmic Sobolev inequality (LSI) and the entropy "sandwich" lemma, extending the analysis from arXiv:2201.10469 and arXiv:2202.01009. The major challenge in the proof via LSI is to show that the relative Fisher information $I(\cdot|\pi)$ is well-defined at every step of the scheme. Since the relative entropy is not Wasserstein differentiable, we prove that along the scheme the iterates belong to a certain class of Sobolev regularity, and hence the relative entropy $\operatorname{KL}(\cdot|\pi)$ has a unique Wasserstein sub-gradient, and that the relative Fisher information is indeed finite.

Mirror Descent-Ascent for mean-field min-max problems

We study two variants of the mirror descent-ascent algorithm for solving min-max problems on the space of measures: simultaneous and sequential. We work under assumptions of convexity-concavity and relative smoothness of the payoff function with respect to a suitable Bregman divergence, defined on the space of measures via flat derivatives. We show that the convergence rates to mixed Nash equilibria, measured in the Nikaid\`o-Isoda error, are of order $\mathcal{O}\left(N^{-1/2}\right)$ and $\mathcal{O}\left(N^{-2/3}\right)$ for the simultaneous and sequential schemes, respectively, which is in line with the state-of-the-art results for related finite-dimensional algorithms.

Multi-index Antithetic Stochastic Gradient Algorithm

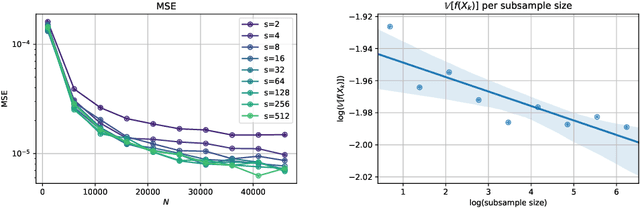
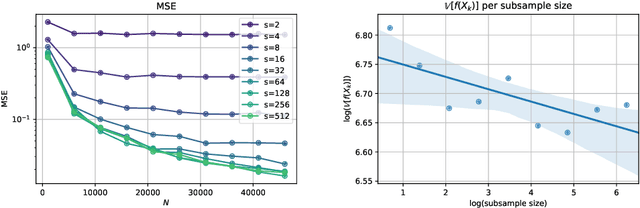
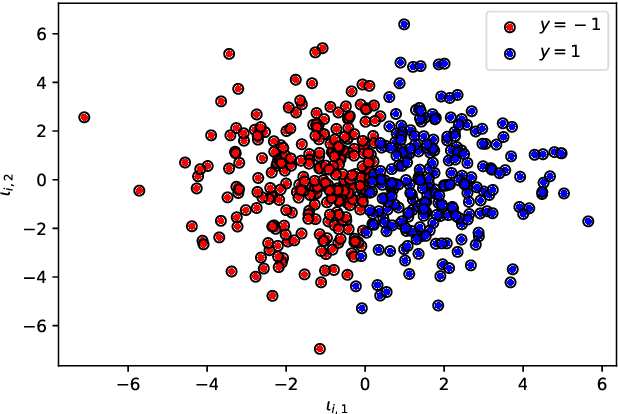
Stochastic Gradient Algorithms (SGAs) are ubiquitous in computational statistics, machine learning and optimisation. Recent years have brought an influx of interest in SGAs and the non-asymptotic analysis of their bias is by now well-developed. However, in order to fully understand the efficiency of Monte Carlo algorithms utilizing stochastic gradients, one also needs to carry out the analysis of their variance, which turns out to be problem-specific. For this reason, there is no systematic theory that would specify the optimal choice of the random approximation of the gradient in SGAs for a given data regime. Furthermore, while there have been numerous attempts to reduce the variance of SGAs, these typically exploit a particular structure of the sampled distribution. In this paper we use the Multi-index Monte Carlo apparatus combined with the antithetic approach to construct the Multi-index Antithetic Stochastic Gradient Algorithm (MASGA), which can be used to sample from any probability distribution. This, to our knowledge, is the first SGA that, for all data regimes and without relying on any specific structure of the target measure, achieves performance on par with Monte Carlo estimators that have access to unbiased samples from the distribution of interest. In other words, MASGA is an optimal estimator from the error-computational cost perspective within the class of Monte Carlo estimators.

Non-asymptotic bounds for sampling algorithms without log-concavity

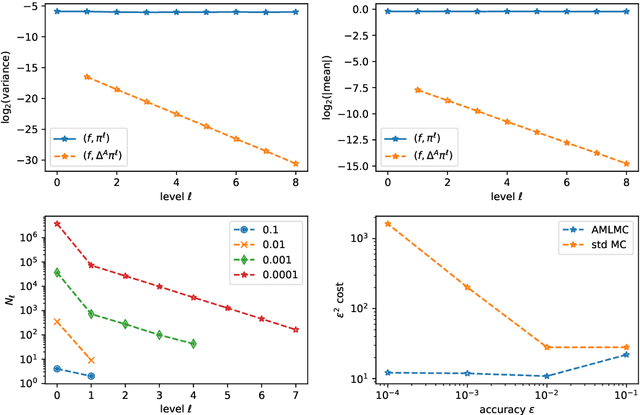
Discrete time analogues of ergodic stochastic differential equations (SDEs) are one of the most popular and flexible tools for sampling high-dimensional probability measures. Non-asymptotic analysis in the $L^2$ Wasserstein distance of sampling algorithms based on Euler discretisations of SDEs has been recently developed by several authors for log-concave probability distributions. In this work we replace the log-concavity assumption with a log-concavity at infinity condition. We provide novel $L^2$ convergence rates for Euler schemes, expressed explicitly in terms of problem parameters. From there we derive non-asymptotic bounds on the distance between the laws induced by Euler schemes and the invariant laws of SDEs, both for schemes with standard and with randomised (inaccurate) drifts. We also obtain bounds for the hierarchy of discretisation, which enables us to deploy a multi-level Monte Carlo estimator. Our proof relies on a novel construction of a coupling for the Markov chains that can be used to control both the $L^1$ and $L^2$ Wasserstein distances simultaneously. Finally, we provide a weak convergence analysis that covers both the standard and the randomised (inaccurate) drift case. In particular, we reveal that the variance of the randomised drift does not influence the rate of weak convergence of the Euler scheme to the SDE.