PPO in the Fisher-Rao geometry

Proximal Policy Optimization (PPO) has become a widely adopted algorithm for reinforcement learning, offering a practical policy gradient method with strong empirical performance. Despite its popularity, PPO lacks formal theoretical guarantees for policy improvement and convergence. PPO is motivated by Trust Region Policy Optimization (TRPO) that utilizes a surrogate loss with a KL divergence penalty, which arises from linearizing the value function within a flat geometric space. In this paper, we derive a tighter surrogate in the Fisher-Rao (FR) geometry, yielding a novel variant, Fisher-Rao PPO (FR-PPO). Our proposed scheme provides strong theoretical guarantees, including monotonic policy improvement. Furthermore, in the tabular setting, we demonstrate that FR-PPO achieves sub-linear convergence without any dependence on the dimensionality of the action or state spaces, marking a significant step toward establishing formal convergence results for PPO-based algorithms.

Linear convergence of proximal descent schemes on the Wasserstein space

We investigate proximal descent methods, inspired by the minimizing movement scheme introduced by Jordan, Kinderlehrer and Otto, for optimizing entropy-regularized functionals on the Wasserstein space. We establish linear convergence under flat convexity assumptions, thereby relaxing the common reliance on geodesic convexity. Our analysis circumvents the need for discrete-time adaptations of the Evolution Variational Inequality (EVI). Instead, we leverage a uniform logarithmic Sobolev inequality (LSI) and the entropy "sandwich" lemma, extending the analysis from arXiv:2201.10469 and arXiv:2202.01009. The major challenge in the proof via LSI is to show that the relative Fisher information $I(\cdot|\pi)$ is well-defined at every step of the scheme. Since the relative entropy is not Wasserstein differentiable, we prove that along the scheme the iterates belong to a certain class of Sobolev regularity, and hence the relative entropy $\operatorname{KL}(\cdot|\pi)$ has a unique Wasserstein sub-gradient, and that the relative Fisher information is indeed finite.

Understanding Transfer Learning via Mean-field Analysis

We propose a novel framework for exploring generalization errors of transfer learning through the lens of differential calculus on the space of probability measures. In particular, we consider two main transfer learning scenarios, $\alpha$-ERM and fine-tuning with the KL-regularized empirical risk minimization and establish generic conditions under which the generalization error and the population risk convergence rates for these scenarios are studied. Based on our theoretical results, we show the benefits of transfer learning with a one-hidden-layer neural network in the mean-field regime under some suitable integrability and regularity assumptions on the loss and activation functions.

Mirror Descent-Ascent for mean-field min-max problems

We study two variants of the mirror descent-ascent algorithm for solving min-max problems on the space of measures: simultaneous and sequential. We work under assumptions of convexity-concavity and relative smoothness of the payoff function with respect to a suitable Bregman divergence, defined on the space of measures via flat derivatives. We show that the convergence rates to mixed Nash equilibria, measured in the Nikaid\`o-Isoda error, are of order $\mathcal{O}\left(N^{-1/2}\right)$ and $\mathcal{O}\left(N^{-2/3}\right)$ for the simultaneous and sequential schemes, respectively, which is in line with the state-of-the-art results for related finite-dimensional algorithms.

Generalization Error of Graph Neural Networks in the Mean-field Regime

This work provides a theoretical framework for assessing the generalization error of graph classification tasks via graph neural networks in the over-parameterized regime, where the number of parameters surpasses the quantity of data points. We explore two widely utilized types of graph neural networks: graph convolutional neural networks and message passing graph neural networks. Prior to this study, existing bounds on the generalization error in the over-parametrized regime were uninformative, limiting our understanding of over-parameterized network performance. Our novel approach involves deriving upper bounds within the mean-field regime for evaluating the generalization error of these graph neural networks. We establish upper bounds with a convergence rate of $O(1/n)$, where $n$ is the number of graph samples. These upper bounds offer a theoretical assurance of the networks' performance on unseen data in the challenging over-parameterized regime and overall contribute to our understanding of their performance.

Mean-field Analysis of Generalization Errors

We propose a novel framework for exploring weak and $L_2$ generalization errors of algorithms through the lens of differential calculus on the space of probability measures. Specifically, we consider the KL-regularized empirical risk minimization problem and establish generic conditions under which the generalization error convergence rate, when training on a sample of size $n$, is $\mathcal{O}(1/n)$. In the context of supervised learning with a one-hidden layer neural network in the mean-field regime, these conditions are reflected in suitable integrability and regularity assumptions on the loss and activation functions.

Multi-index Antithetic Stochastic Gradient Algorithm

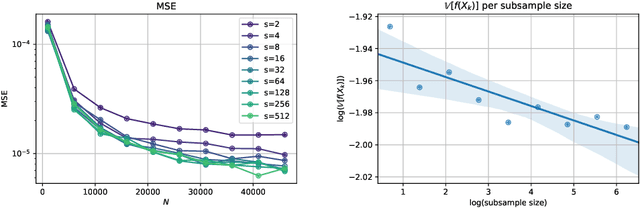
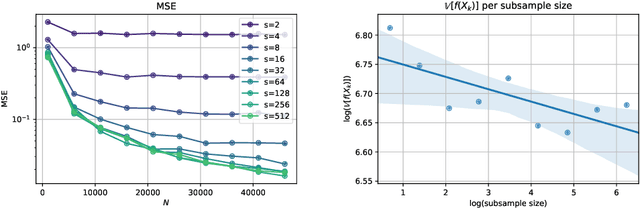
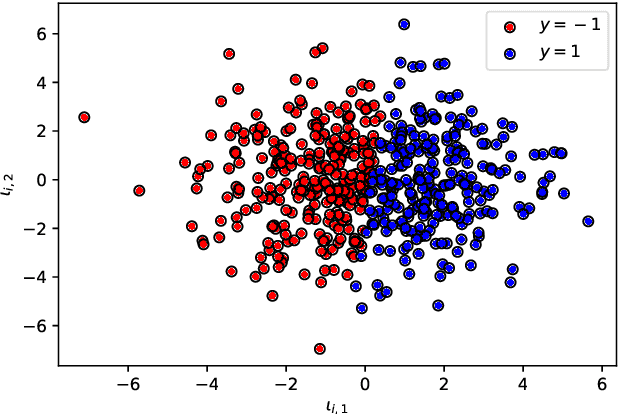
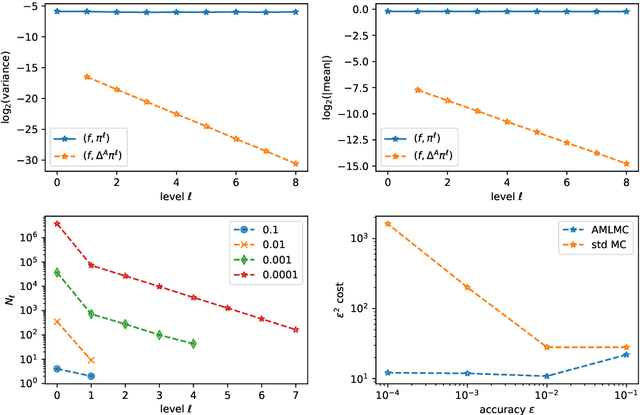
Stochastic Gradient Algorithms (SGAs) are ubiquitous in computational statistics, machine learning and optimisation. Recent years have brought an influx of interest in SGAs and the non-asymptotic analysis of their bias is by now well-developed. However, in order to fully understand the efficiency of Monte Carlo algorithms utilizing stochastic gradients, one also needs to carry out the analysis of their variance, which turns out to be problem-specific. For this reason, there is no systematic theory that would specify the optimal choice of the random approximation of the gradient in SGAs for a given data regime. Furthermore, while there have been numerous attempts to reduce the variance of SGAs, these typically exploit a particular structure of the sampled distribution. In this paper we use the Multi-index Monte Carlo apparatus combined with the antithetic approach to construct the Multi-index Antithetic Stochastic Gradient Algorithm (MASGA), which can be used to sample from any probability distribution. This, to our knowledge, is the first SGA that, for all data regimes and without relying on any specific structure of the target measure, achieves performance on par with Monte Carlo estimators that have access to unbiased samples from the distribution of interest. In other words, MASGA is an optimal estimator from the error-computational cost perspective within the class of Monte Carlo estimators.

Gradient Flows for Regularized Stochastic Control Problems

This work is motivated by a desire to extend the theoretical underpinning for the convergence of stochastic gradient type algorithms widely used in the reinforcement learning community to solve control problems. This paper studies stochastic control problems regularized by the relative entropy, where the action space is the space of measures. This setting includes relaxed control problems, problems of finding Markovian controls with the control function replaced by an idealized infinitely wide neural network and can be extended to the search for causal optimal transport maps. By exploiting the Pontryagin optimality principle, we construct gradient flow for the measure-valued control process along which the cost functional is guaranteed to decrease. It is shown that under appropriate conditions, this gradient flow has an invariant measure which is the optimal control for the regularized stochastic control problem. If the problem we work with is sufficiently convex, the gradient flow converges exponentially fast.

Mean-Field Neural ODEs via Relaxed Optimal Control

We develop a framework for the analysis of deep neural networks and neural ODE models that are trained with stochastic gradient algorithms. We do that by identifying the connections between high-dimensional data-driven control problems, deep learning and theory of statistical sampling. In particular, we derive and study a mean-field (over-damped) Langevin algorithm for solving relaxed data-driven control problems. A key step in the analysis is to derive Pontryagin's optimality principle for data-driven relaxed control problems. Subsequently, we study uniform-in-time propagation of chaos of time-discretised Mean-Field (overdamped) Langevin dynamics. We derive explicit convergence rate in terms of the learning rate, the number of particles/model parameters and the number of iterations of the gradient algorithm. In addition, we study the error arising when using a finite training data set and thus provide quantitive bounds on the generalisation error. Crucially, the obtained rates are dimension-independent. This is possible by exploiting the regularity of the model with respect to the measure over the parameter space (relaxed control).