Linear convergence of proximal descent schemes on the Wasserstein space

We investigate proximal descent methods, inspired by the minimizing movement scheme introduced by Jordan, Kinderlehrer and Otto, for optimizing entropy-regularized functionals on the Wasserstein space. We establish linear convergence under flat convexity assumptions, thereby relaxing the common reliance on geodesic convexity. Our analysis circumvents the need for discrete-time adaptations of the Evolution Variational Inequality (EVI). Instead, we leverage a uniform logarithmic Sobolev inequality (LSI) and the entropy "sandwich" lemma, extending the analysis from arXiv:2201.10469 and arXiv:2202.01009. The major challenge in the proof via LSI is to show that the relative Fisher information $I(\cdot|\pi)$ is well-defined at every step of the scheme. Since the relative entropy is not Wasserstein differentiable, we prove that along the scheme the iterates belong to a certain class of Sobolev regularity, and hence the relative entropy $\operatorname{KL}(\cdot|\pi)$ has a unique Wasserstein sub-gradient, and that the relative Fisher information is indeed finite.

Entropy annealing for policy mirror descent in continuous time and space

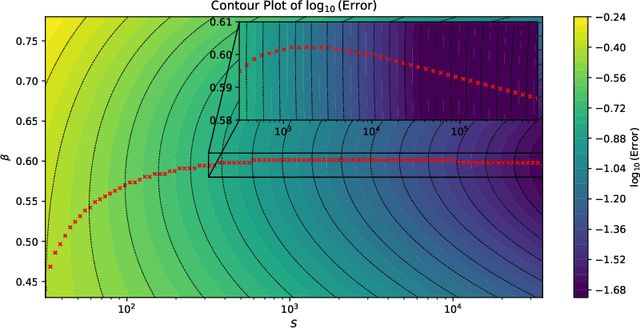
Entropy regularization has been extensively used in policy optimization algorithms to regularize the optimization landscape and accelerate convergence; however, it comes at the cost of introducing an additional regularization bias. This work quantifies the impact of entropy regularization on the convergence of policy gradient methods for stochastic exit time control problems. We analyze a continuous-time policy mirror descent dynamics, which updates the policy based on the gradient of an entropy-regularized value function and adjusts the strength of entropy regularization as the algorithm progresses. We prove that with a fixed entropy level, the dynamics converges exponentially to the optimal solution of the regularized problem. We further show that when the entropy level decays at suitable polynomial rates, the annealed flow converges to the solution of the unregularized problem at a rate of $\mathcal O(1/S)$ for discrete action spaces and, under suitable conditions, at a rate of $\mathcal O(1/\sqrt{S})$ for general action spaces, with $S$ being the gradient flow time. This paper explains how entropy regularization improves policy optimization, even with the true gradient, from the perspective of convergence rate.

Convergence of policy gradient for entropy regularized MDPs with neural network approximation in the mean-field regime

We study the global convergence of policy gradient for infinite-horizon, continuous state and action space, entropy-regularized Markov decision processes (MDPs). We consider a softmax policy with (one-hidden layer) neural network approximation in a mean-field regime. Additional entropic regularization in the associated mean-field probability measure is added, and the corresponding gradient flow is studied in the 2-Wasserstein metric. We show that the objective function is increasing along the gradient flow. Further, we prove that if the regularization in terms of the mean-field measure is sufficient, the gradient flow converges exponentially fast to the unique stationary solution, which is the unique maximizer of the regularized MDP objective. Lastly, we study the sensitivity of the value function along the gradient flow with respect to regularization parameters and the initial condition. Our results rely on the careful analysis of non-linear Fokker--Planck--Kolmogorov equation and extend the pioneering work of Mei et al. 2020 and Agarwal et al. 2020, which quantify the global convergence rate of policy gradient for entropy-regularized MDPs in the tabular setting.

Robust pricing and hedging via neural SDEs

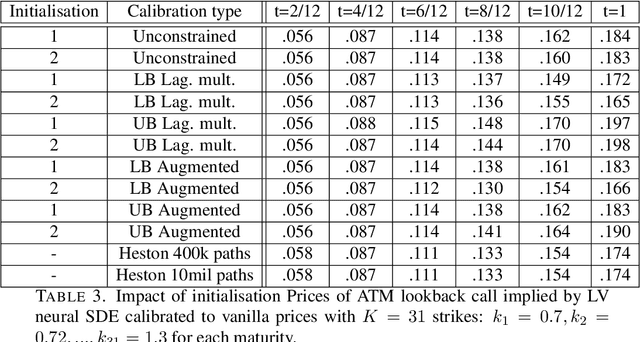
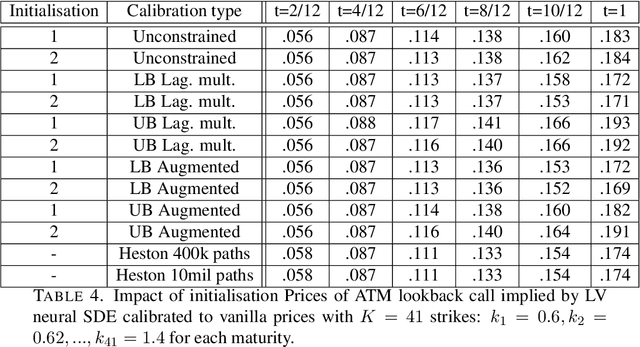
Mathematical modelling is ubiquitous in the financial industry and drives key decision processes. Any given model provides only a crude approximation to reality and the risk of using an inadequate model is hard to detect and quantify. By contrast, modern data science techniques are opening the door to more robust and data-driven model selection mechanisms. However, most machine learning models are "black-boxes" as individual parameters do not have meaningful interpretation. The aim of this paper is to combine the above approaches achieving the best of both worlds. Combining neural networks with risk models based on classical stochastic differential equations (SDEs), we find robust bounds for prices of derivatives and the corresponding hedging strategies while incorporating relevant market data. The resulting model called neural SDE is an instantiation of generative models and is closely linked with the theory of causal optimal transport. Neural SDEs allow consistent calibration under both the risk-neutral and the real-world measures. Thus the model can be used to simulate market scenarios needed for assessing risk profiles and hedging strategies. We develop and analyse novel algorithms needed for efficient use of neural SDEs. We validate our approach with numerical experiments using both local and stochastic volatility models.

Gradient Flows for Regularized Stochastic Control Problems

This work is motivated by a desire to extend the theoretical underpinning for the convergence of stochastic gradient type algorithms widely used in the reinforcement learning community to solve control problems. This paper studies stochastic control problems regularized by the relative entropy, where the action space is the space of measures. This setting includes relaxed control problems, problems of finding Markovian controls with the control function replaced by an idealized infinitely wide neural network and can be extended to the search for causal optimal transport maps. By exploiting the Pontryagin optimality principle, we construct gradient flow for the measure-valued control process along which the cost functional is guaranteed to decrease. It is shown that under appropriate conditions, this gradient flow has an invariant measure which is the optimal control for the regularized stochastic control problem. If the problem we work with is sufficiently convex, the gradient flow converges exponentially fast.

Mean-Field Neural ODEs via Relaxed Optimal Control

We develop a framework for the analysis of deep neural networks and neural ODE models that are trained with stochastic gradient algorithms. We do that by identifying the connections between high-dimensional data-driven control problems, deep learning and theory of statistical sampling. In particular, we derive and study a mean-field (over-damped) Langevin algorithm for solving relaxed data-driven control problems. A key step in the analysis is to derive Pontryagin's optimality principle for data-driven relaxed control problems. Subsequently, we study uniform-in-time propagation of chaos of time-discretised Mean-Field (overdamped) Langevin dynamics. We derive explicit convergence rate in terms of the learning rate, the number of particles/model parameters and the number of iterations of the gradient algorithm. In addition, we study the error arising when using a finite training data set and thus provide quantitive bounds on the generalisation error. Crucially, the obtained rates are dimension-independent. This is possible by exploiting the regularity of the model with respect to the measure over the parameter space (relaxed control).

Uniform error estimates for artificial neural network approximations for heat equations

Recently, artificial neural networks (ANNs) in conjunction with stochastic gradient descent optimization methods have been employed to approximately compute solutions of possibly rather high-dimensional partial differential equations (PDEs). Very recently, there have also been a number of rigorous mathematical results in the scientific literature which examine the approximation capabilities of such deep learning based approximation algorithms for PDEs. These mathematical results from the scientific literature prove in part that algorithms based on ANNs are capable of overcoming the curse of dimensionality in the numerical approximation of high-dimensional PDEs. In these mathematical results from the scientific literature usually the error between the solution of the PDE and the approximating ANN is measured in the $L^p$-sense with respect to some $p \in [1,\infty)$ and some probability measure. In many applications it is, however, also important to control the error in a uniform $L^\infty$-sense. The key contribution of the main result of this article is to develop the techniques to obtain error estimates between solutions of PDEs and approximating ANNs in the uniform $L^\infty$-sense. In particular, we prove that the number of parameters of an ANN to uniformly approximate the classical solution of the heat equation in a region $ [a,b]^d $ for a fixed time point $ T \in (0,\infty) $ grows at most polynomially in the dimension $ d \in \mathbb{N} $ and the reciprocal of the approximation precision $ \varepsilon > 0 $. This shows that ANNs can overcome the curse of dimensionality in the numerical approximation of the heat equation when the error is measured in the uniform $L^\infty$-norm.