PADAM: Parallel averaged Adam reduces the error for stochastic optimization in scientific machine learning

Averaging techniques such as Ruppert--Polyak averaging and exponential movering averaging (EMA) are powerful approaches to accelerate optimization procedures of stochastic gradient descent (SGD) optimization methods such as the popular ADAM optimizer. However, depending on the specific optimization problem under consideration, the type and the parameters for the averaging need to be adjusted to achieve the smallest optimization error. In this work we propose an averaging approach, which we refer to as parallel averaged ADAM (PADAM), in which we compute parallely different averaged variants of ADAM and during the training process dynamically select the variant with the smallest optimization error. A central feature of this approach is that this procedure requires no more gradient evaluations than the usual ADAM optimizer as each of the averaged trajectories relies on the same underlying ADAM trajectory and thus on the same underlying gradients. We test the proposed PADAM optimizer in 13 stochastic optimization and deep neural network (DNN) learning problems and compare its performance with known optimizers from the literature such as standard SGD, momentum SGD, Adam with and without EMA, and ADAMW. In particular, we apply the compared optimizers to physics-informed neural network, deep Galerkin, deep backward stochastic differential equation and deep Kolmogorov approximations for boundary value partial differential equation problems from scientific machine learning, as well as to DNN approximations for optimal control and optimal stopping problems. In nearly all of the considered examples PADAM achieves, sometimes among others and sometimes exclusively, essentially the smallest optimization error. This work thus strongly suggest to consider PADAM for scientific machine learning problems and also motivates further research for adaptive averaging procedures within the training of DNNs.

SAD Neural Networks: Divergent Gradient Flows and Asymptotic Optimality via o-minimal Structures

We study gradient flows for loss landscapes of fully connected feed forward neural networks with commonly used continuously differentiable activation functions such as the logistic, hyperbolic tangent, softplus or GELU function. We prove that the gradient flow either converges to a critical point or diverges to infinity while the loss converges to an asymptotic critical value. Moreover, we prove the existence of a threshold $\varepsilon>0$ such that the loss value of any gradient flow initialized at most $\varepsilon$ above the optimal level converges to it. For polynomial target functions and sufficiently big architecture and data set, we prove that the optimal loss value is zero and can only be realized asymptotically. From this setting, we deduce our main result that any gradient flow with sufficiently good initialization diverges to infinity. Our proof heavily relies on the geometry of o-minimal structures. We confirm these theoretical findings with numerical experiments and extend our investigation to real-world scenarios, where we observe an analogous behavior.

Sharp higher order convergence rates for the Adam optimizer

Gradient descent based optimization methods are the methods of choice to train deep neural networks in machine learning. Beyond the standard gradient descent method, also suitable modified variants of standard gradient descent involving acceleration techniques such as the momentum method and/or adaptivity techniques such as the RMSprop method are frequently considered optimization methods. These days the most popular of such sophisticated optimization schemes is presumably the Adam optimizer that has been proposed in 2014 by Kingma and Ba. A highly relevant topic of research is to investigate the speed of convergence of such optimization methods. In particular, in 1964 Polyak showed that the standard gradient descent method converges in a neighborhood of a strict local minimizer with rate (x - 1)(x + 1)^{-1} while momentum achieves the (optimal) strictly faster convergence rate (\sqrt{x} - 1)(\sqrt{x} + 1)^{-1} where x \in (1,\infty) is the condition number (the ratio of the largest and the smallest eigenvalue) of the Hessian of the objective function at the local minimizer. It is the key contribution of this work to reveal that Adam also converges with the strictly faster convergence rate (\sqrt{x} - 1)(\sqrt{x} + 1)^{-1} while RMSprop only converges with the convergence rate (x - 1)(x + 1)^{-1}.

Non-convergence to the optimal risk for Adam and stochastic gradient descent optimization in the training of deep neural networks

Despite the omnipresent use of stochastic gradient descent (SGD) optimization methods in the training of deep neural networks (DNNs), it remains, in basically all practically relevant scenarios, a fundamental open problem to provide a rigorous theoretical explanation for the success (and the limitations) of SGD optimization methods in deep learning. In particular, it remains an open question to prove or disprove convergence of the true risk of SGD optimization methods to the optimal true risk value in the training of DNNs. In one of the main results of this work we reveal for a general class of activations, loss functions, random initializations, and SGD optimization methods (including, for example, standard SGD, momentum SGD, Nesterov accelerated SGD, Adagrad, RMSprop, Adadelta, Adam, Adamax, Nadam, Nadamax, and AMSGrad) that in the training of any arbitrary fully-connected feedforward DNN it does not hold that the true risk of the considered optimizer converges in probability to the optimal true risk value. Nonetheless, the true risk of the considered SGD optimization method may very well converge to a strictly suboptimal true risk value.

On the logical skills of large language models: evaluations using arbitrarily complex first-order logic problems

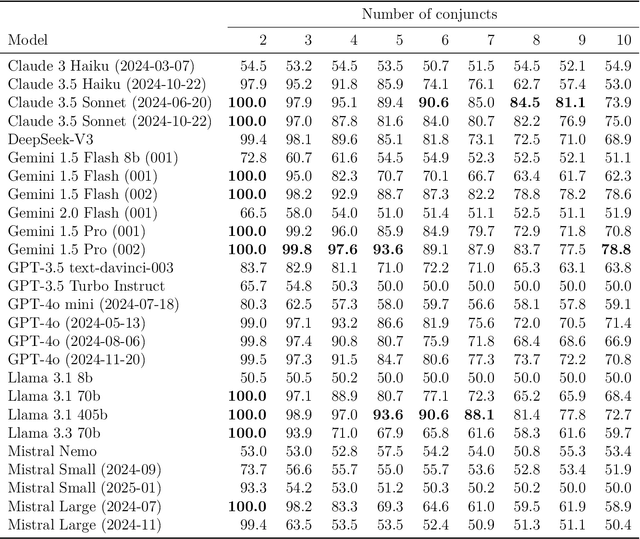
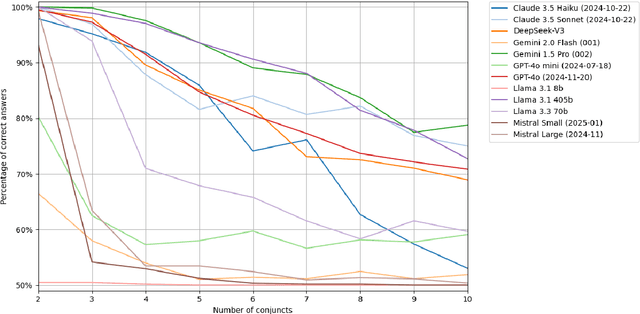
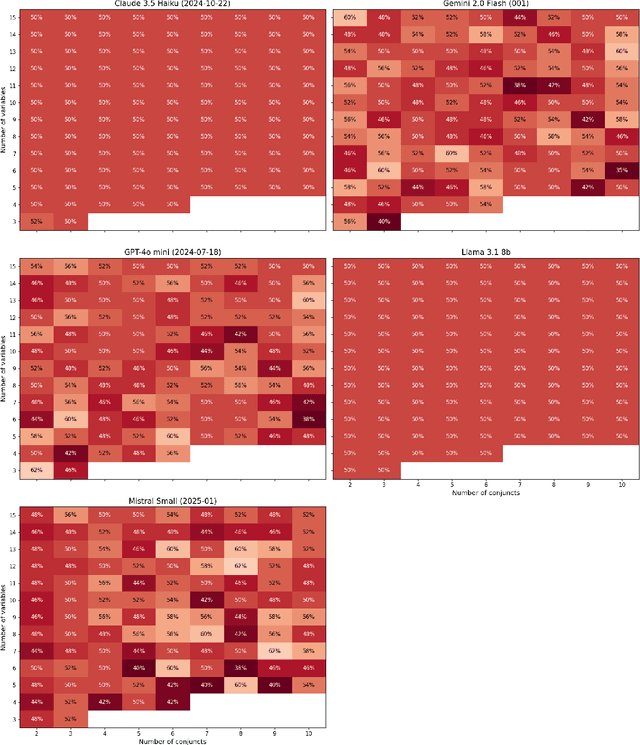
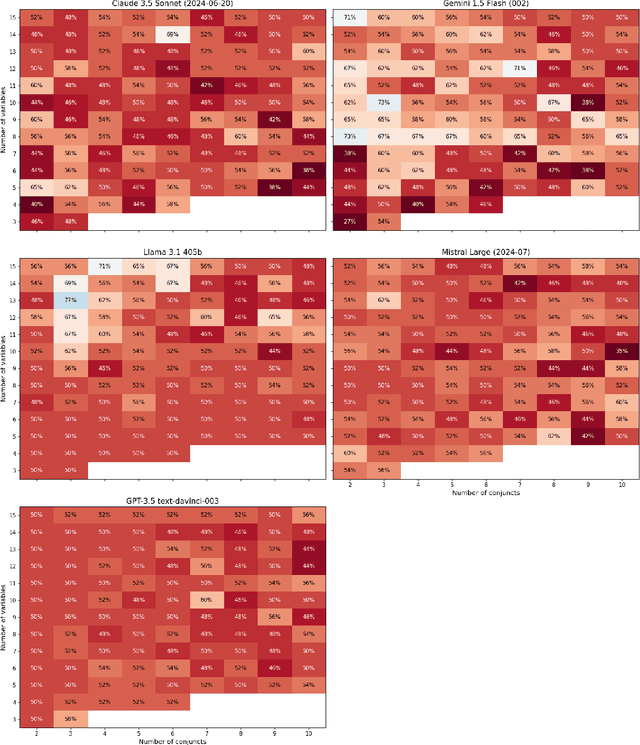
We present a method of generating first-order logic statements whose complexity can be controlled along multiple dimensions. We use this method to automatically create several datasets consisting of questions asking for the truth or falsity of first-order logic statements in Zermelo-Fraenkel set theory. While the resolution of these questions does not require any knowledge beyond basic notation of first-order logic and set theory, it does require a degree of planning and logical reasoning, which can be controlled up to arbitrarily high difficulty by the complexity of the generated statements. Furthermore, we do extensive evaluations of the performance of various large language models, including recent models such as DeepSeek-R1 and OpenAI's o3-mini, on these datasets. All of the datasets along with the code used for generating them, as well as all data from the evaluations is publicly available at https://github.com/bkuckuck/logical-skills-of-llms.

Mathematical analysis of the gradients in deep learning

Deep learning algorithms -- typically consisting of a class of deep artificial neural networks (ANNs) trained by a stochastic gradient descent (SGD) optimization method -- are nowadays an integral part in many areas of science, industry, and also our day to day life. Roughly speaking, in their most basic form, ANNs can be regarded as functions that consist of a series of compositions of affine-linear functions with multidimensional versions of so-called activation functions. One of the most popular of such activation functions is the rectified linear unit (ReLU) function $\mathbb{R} \ni x \mapsto \max\{ x, 0 \} \in \mathbb{R}$. The ReLU function is, however, not differentiable and, typically, this lack of regularity transfers to the cost function of the supervised learning problem under consideration. Regardless of this lack of differentiability issue, deep learning practioners apply SGD methods based on suitably generalized gradients in standard deep learning libraries like {\sc TensorFlow} or {\sc Pytorch}. In this work we reveal an accurate and concise mathematical description of such generalized gradients in the training of deep fully-connected feedforward ANNs and we also study the resulting generalized gradient function analytically. Specifically, we provide an appropriate approximation procedure that uniquely describes the generalized gradient function, we prove that the generalized gradients are limiting Fr\'echet subgradients of the cost functional, and we conclude that the generalized gradients must coincide with the standard gradient of the cost functional on every open sets on which the cost functional is continuously differentiable.

Averaged Adam accelerates stochastic optimization in the training of deep neural network approximations for partial differential equation and optimal control problems

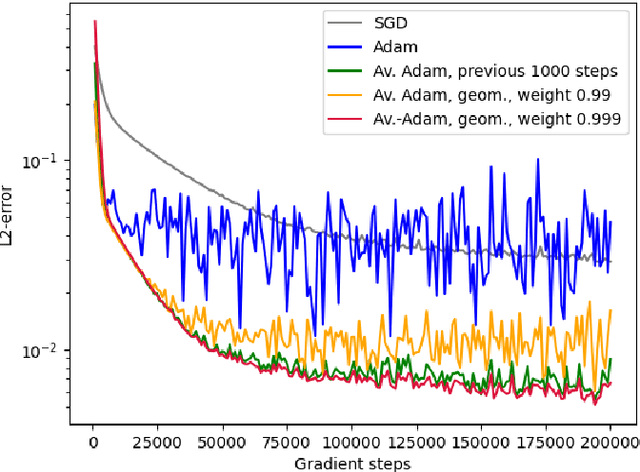
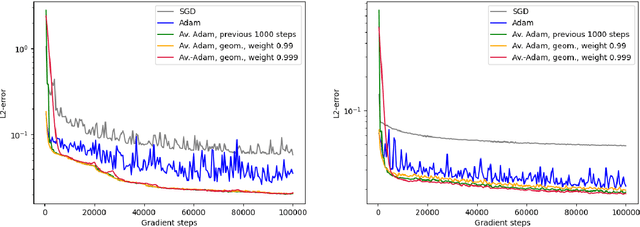
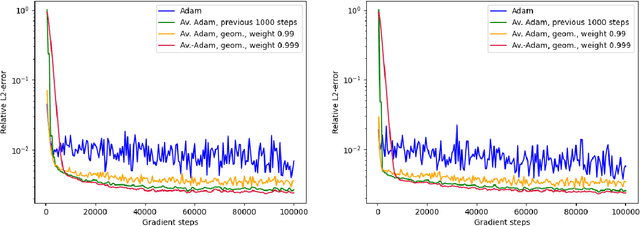
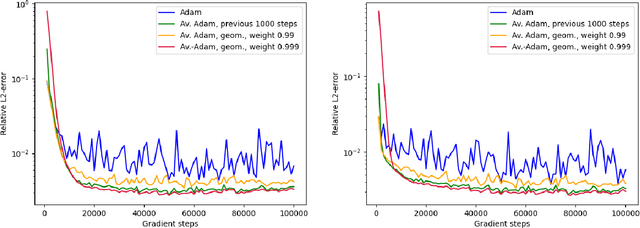
Deep learning methods - usually consisting of a class of deep neural networks (DNNs) trained by a stochastic gradient descent (SGD) optimization method - are nowadays omnipresent in data-driven learning problems as well as in scientific computing tasks such as optimal control (OC) and partial differential equation (PDE) problems. In practically relevant learning tasks, often not the plain-vanilla standard SGD optimization method is employed to train the considered class of DNNs but instead more sophisticated adaptive and accelerated variants of the standard SGD method such as the popular Adam optimizer are used. Inspired by the classical Polyak-Ruppert averaging approach, in this work we apply averaged variants of the Adam optimizer to train DNNs to approximately solve exemplary scientific computing problems in the form of PDEs and OC problems. We test the averaged variants of Adam in a series of learning problems including physics-informed neural network (PINN), deep backward stochastic differential equation (deep BSDE), and deep Kolmogorov approximations for PDEs (such as heat, Black-Scholes, Burgers, and Allen-Cahn PDEs), including DNN approximations for OC problems, and including DNN approximations for image classification problems (ResNet for CIFAR-10). In each of the numerical examples the employed averaged variants of Adam outperform the standard Adam and the standard SGD optimizers, particularly, in the situation of the scientific machine learning problems. The Python source codes for the numerical experiments associated to this work can be found on GitHub at https://github.com/deeplearningmethods/averaged-adam.

An overview of diffusion models for generative artificial intelligence

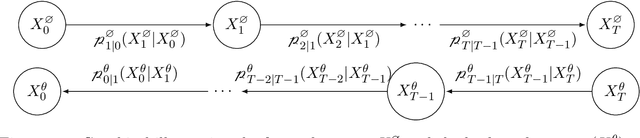
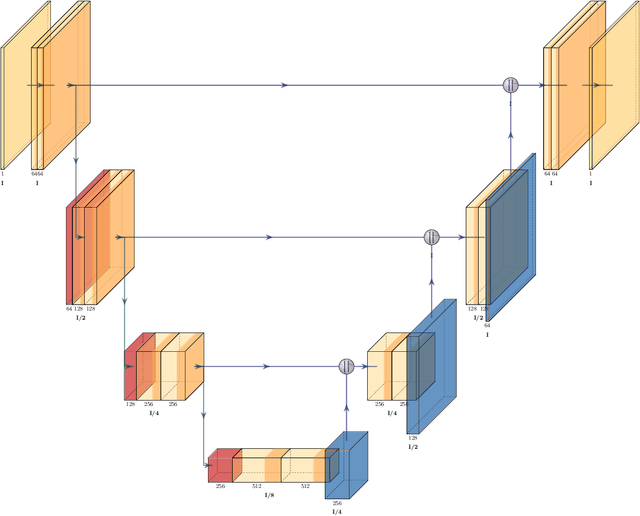
This article provides a mathematically rigorous introduction to denoising diffusion probabilistic models (DDPMs), sometimes also referred to as diffusion probabilistic models or diffusion models, for generative artificial intelligence. We provide a detailed basic mathematical framework for DDPMs and explain the main ideas behind training and generation procedures. In this overview article we also review selected extensions and improvements of the basic framework from the literature such as improved DDPMs, denoising diffusion implicit models, classifier-free diffusion guidance models, and latent diffusion models.

Non-convergence to global minimizers in data driven supervised deep learning: Adam and stochastic gradient descent optimization provably fail to converge to global minimizers in the training of deep neural networks with ReLU activation

Deep learning methods - consisting of a class of deep neural networks (DNNs) trained by a stochastic gradient descent (SGD) optimization method - are nowadays key tools to solve data driven supervised learning problems. Despite the great success of SGD methods in the training of DNNs, it remains a fundamental open problem of research to explain the success and the limitations of such methods in rigorous theoretical terms. In particular, even in the standard setup of data driven supervised learning problems, it remained an open research problem to prove (or disprove) that SGD methods converge in the training of DNNs with the popular rectified linear unit (ReLU) activation function with high probability to global minimizers in the optimization landscape. In this work we answer this question negatively. Specifically, in this work we prove for a large class of SGD methods that the considered optimizer does with high probability not converge to global minimizers of the optimization problem. It turns out that the probability to not converge to a global minimizer converges at least exponentially quickly to one as the width of the first hidden layer of the ANN and the depth of the ANN, respectively, increase. The general non-convergence results of this work do not only apply to the plain vanilla standard SGD method but also to a large class of accelerated and adaptive SGD methods such as the momentum SGD, the Nesterov accelerated SGD, the Adagrad, the RMSProp, the Adam, the Adamax, the AMSGrad, and the Nadam optimizers.

An Overview on Machine Learning Methods for Partial Differential Equations: from Physics Informed Neural Networks to Deep Operator Learning

The approximation of solutions of partial differential equations (PDEs) with numerical algorithms is a central topic in applied mathematics. For many decades, various types of methods for this purpose have been developed and extensively studied. One class of methods which has received a lot of attention in recent years are machine learning-based methods, which typically involve the training of artificial neural networks (ANNs) by means of stochastic gradient descent type optimization methods. While approximation methods for PDEs using ANNs have first been proposed in the 1990s they have only gained wide popularity in the last decade with the rise of deep learning. This article aims to provide an introduction to some of these methods and the mathematical theory on which they are based. We discuss methods such as physics-informed neural networks (PINNs) and deep BSDE methods and consider several operator learning approaches.