Interpolation property of shallow neural networks

We study the geometry of global minima of the loss landscape of overparametrized neural networks. In most optimization problems, the loss function is convex, in which case we only have a global minima, or nonconvex, with a discrete number of global minima. In this paper, we prove that in the overparametrized regime, a shallow neural network can interpolate any data set, i.e. the loss function has a global minimum value equal to zero as long as the activation function is not a polynomial of small degree. Additionally, if such a global minimum exists, then the locus of global minima has infinitely many points. Furthermore, we give a characterization of the Hessian of the loss function evaluated at the global minima, and in the last section, we provide a practical probabilistic method of finding the interpolation point.

From Monte Carlo to neural networks approximations of boundary value problems

In this paper we study probabilistic and neural network approximations for solutions to Poisson equation subject to H\" older or $C^2$ data in general bounded domains of $\mathbb{R}^d$. We aim at two fundamental goals. The first, and the most important, we show that the solution to Poisson equation can be numerically approximated in the sup-norm by Monte Carlo methods based on a slight change of the walk on spheres algorithm. This provides estimates which are efficient with respect to the prescribed approximation error and without the curse of dimensionality. In addition, the overall number of samples does not not depend on the point at which the approximation is performed. As a second goal, we show that the obtained Monte Carlo solver renders ReLU deep neural network (DNN) solutions to Poisson problem, whose sizes depend at most polynomially in the dimension $d$ and in the desired error. In fact we show that the random DNN provides with high probability a small approximation error and low polynomial complexity in the dimension.

LoCoV: low dimension covariance voting algorithm for portfolio optimization

Minimum-variance portfolio optimizations rely on accurate covariance estimator to obtain optimal portfolios. However, it usually suffers from large error from sample covariance matrix when the sample size $n$ is not significantly larger than the number of assets $p$. We analyze the random matrix aspects of portfolio optimization and identify the order of errors in sample optimal portfolio weight and show portfolio risk are underestimated when using samples. We also provide LoCoV (low dimension covariance voting) algorithm to reduce error inherited from random samples. From various experiments, LoCoV is shown to outperform the classical method by a large margin.

A Dynamical Estimation and Prediction for Covid19 on Romania using ensemble neural networks

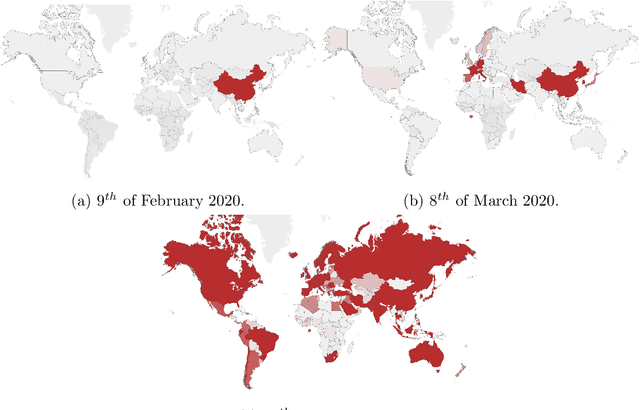
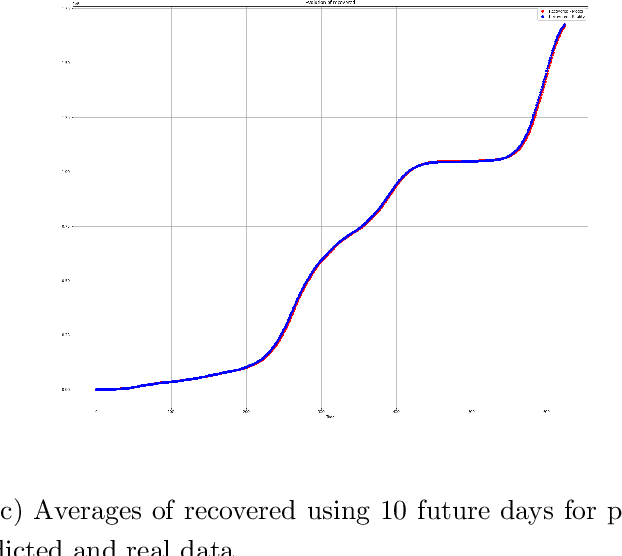
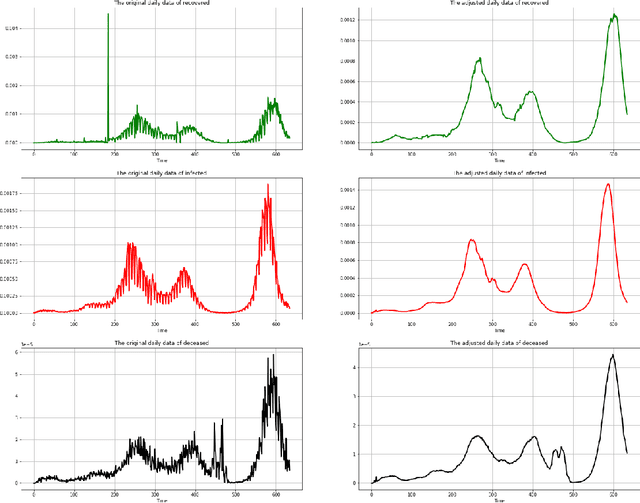
In this paper, we propose an analysis of Covid19 evolution and prediction on Romania combined with the mathematical model of SIRD, an extension of the classical model SIR, which includes the deceased as a separate category. The reason is that, because we can not fully trust the reported numbers of infected or recovered people, we base our analysis on the more reliable number of deceased people. In addition, one of the parameters of our model includes the proportion of infected and tested versus infected. Since there are many factors which have an impact on the evolution of the pandemic, we decide to treat the estimation and the prediction based on the previous 7 days of data, particularly important here being the number of deceased. We perform the estimation and prediction using neural networks in two steps. Firstly, by simulating data with our model, we train several neural networks which learn the parameters of the model. Secondly, we use an ensemble of ten of these neural networks to forecast the parameters from the real data of Covid19 in Romania. Many of these results are backed up by a theorem which guarantees that we can recover the parameters from the reported data.

Recover the spectrum of covariance matrix: a non-asymptotic iterative method

It is well known the sample covariance has a consistent bias in the spectrum, for example spectrum of Wishart matrix follows the Marchenko-Pastur law. We in this work introduce an iterative algorithm 'Concent' that actively eliminate this bias and recover the true spectrum for small and moderate dimensions.

A regime switching on Covid19 analysis and prediction in Romania

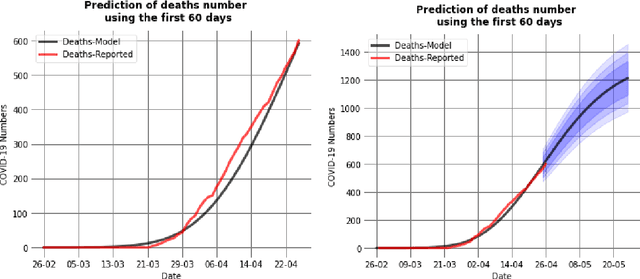
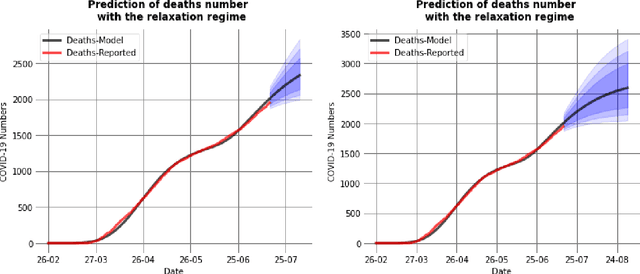
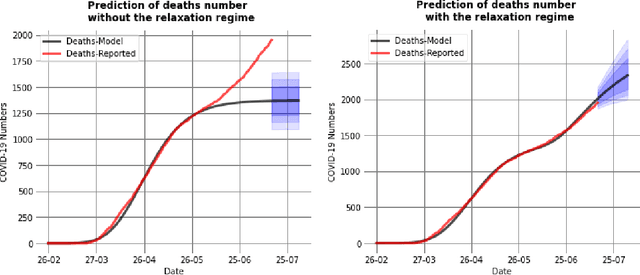
In this paper we propose a regime separation for the analysis of Covid19 on Romania combined with mathematical models of SIR and SIRD. The main regimes we study are, the free spread of the virus, the quarantine and partial relaxation and the last one is the relaxation regime. The main model we use is SIR which is a classical model, but because we can not fully trust the numbers of infected or recovered we base our analysis on the number of deceased people which is more reliable. To actually deal with this we introduce a simple modification of the SIR model to account for the deceased separately. This in turn will be our base for fitting the parameters. The estimation of the parameters is done in two steps. The first one consists in training a neural network based on SIR models to detect the regime changes. Once this is done we fit the main parameters of the SIRD model using a grid search. At the end, we make some predictions on what the evolution will be in a timeframe of a month with the fitted parameters.

A self-supervised neural-analytic method to predict the evolution of COVID-19 in Romania

Analysing and understanding the transmission and evolution of the COVID-19 pandemic is mandatory to be able to design the best social and medical policies, foresee their outcomes and deal with all the subsequent socio-economic effects. We address this important problem from a computational and machine learning perspective. More specifically, we want to statistically estimate all the relevant parameters for the new coronavirus COVID-19, such as the reproduction number, fatality rate or length of infectiousness period, based on Romanian patients, as well as be able to predict future outcomes. This endeavor is important, since it is well known that these factors vary across the globe, and might be dependent on many causes, including social, medical, age and genetic factors. We use a recently published improved version of SEIR, which is the classic, established model for infectious diseases. We want to infer all the parameters of the model, which govern the evolution of the pandemic in Romania, based on the only reliable, true measurement, which is the number of deaths. Once the model parameters are estimated, we are able to predict all the other relevant measures, such as the number of exposed and infectious people. To this end, we propose a self-supervised approach to train a deep convolutional network to guess the correct set of Modified-SEIR model parameters, given the observed number of daily fatalities. Then, we refine the solution with a stochastic coordinate descent approach. We compare our deep learning optimization scheme with the classic grid search approach and show great improvement in both computational time and prediction accuracy. We find an optimistic result in the case fatality rate for Romania which may be around 0.3% and we also demonstrate that our model is able to correctly predict the number of daily fatalities for up to three weeks in the future.

An Analytical Formula for Spectrum Reconstruction

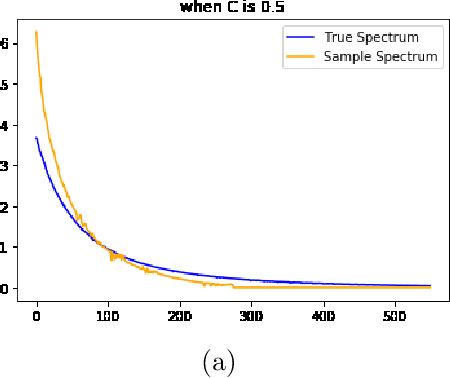
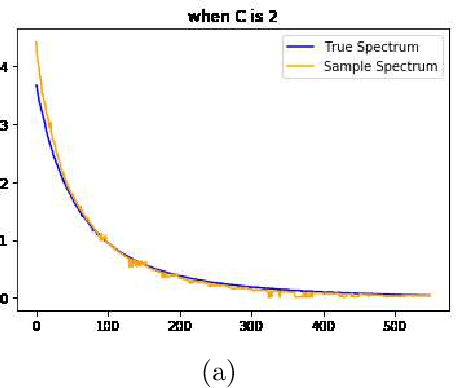
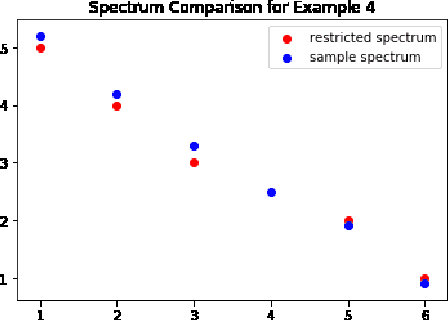
We study the spectrum reconstruction technique. As is known to all, eigenvalues play an important role in many research fields and are foundation to many practical techniques such like PCA(Principal Component Analysis). We believe that related algorithms should perform better with more accurate spectrum estimation. There was an approximation formula proposed, however, they didn't give any proof. In our research, we show why the formula works. And when both number of features and dimension of space go to infinity, we find the order of error for the approximation formula, which is related to a constant $c$-the ratio of dimension of space and number of features.

A cost-reducing partial labeling estimator in text classification problem

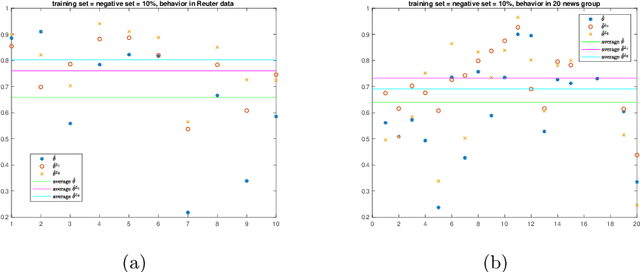
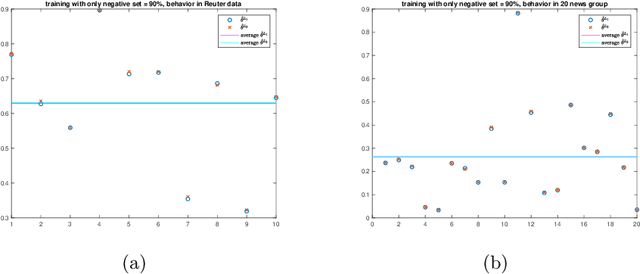
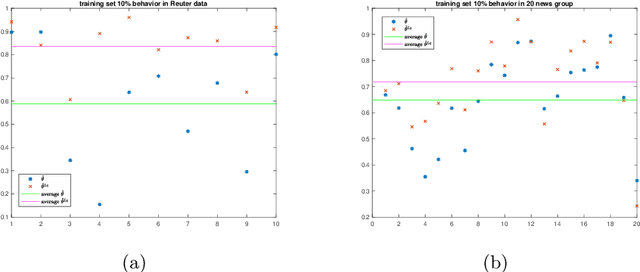
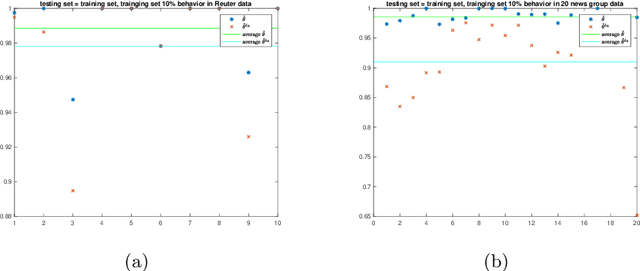
We propose a new approach to address the text classification problems when learning with partial labels is beneficial. Instead of offering each training sample a set of candidate labels, we assign negative-oriented labels to the ambiguous training examples if they are unlikely fall into certain classes. We construct our new maximum likelihood estimators with self-correction property, and prove that under some conditions, our estimators converge faster. Also we discuss the advantages of applying one of our estimator to a fully supervised learning problem. The proposed method has potential applicability in many areas, such as crowdsourcing, natural language processing and medical image analysis.