Brain-JEPA: Brain Dynamics Foundation Model with Gradient Positioning and Spatiotemporal Masking

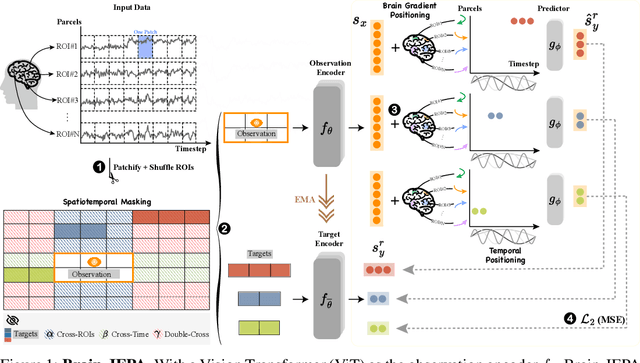
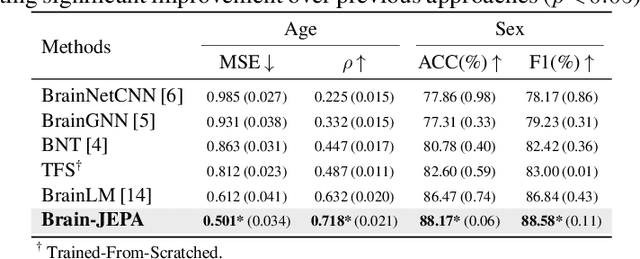
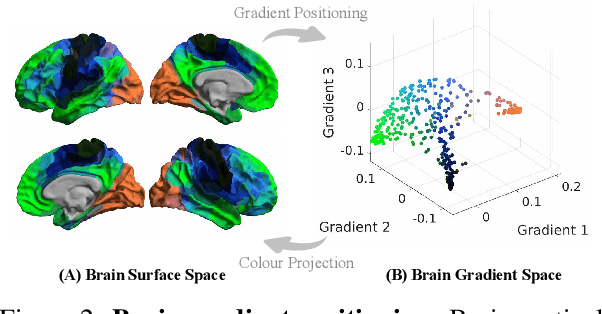
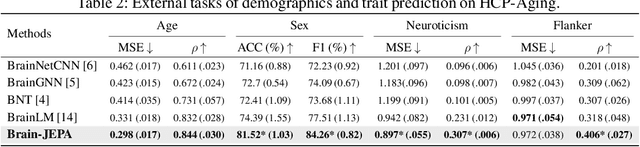
We introduce Brain-JEPA, a brain dynamics foundation model with the Joint-Embedding Predictive Architecture (JEPA). This pioneering model achieves state-of-the-art performance in demographic prediction, disease diagnosis/prognosis, and trait prediction through fine-tuning. Furthermore, it excels in off-the-shelf evaluations (e.g., linear probing) and demonstrates superior generalizability across different ethnic groups, surpassing the previous large model for brain activity significantly. Brain-JEPA incorporates two innovative techniques: Brain Gradient Positioning and Spatiotemporal Masking. Brain Gradient Positioning introduces a functional coordinate system for brain functional parcellation, enhancing the positional encoding of different Regions of Interest (ROIs). Spatiotemporal Masking, tailored to the unique characteristics of fMRI data, addresses the challenge of heterogeneous time-series patches. These methodologies enhance model performance and advance our understanding of the neural circuits underlying cognition. Overall, Brain-JEPA is paving the way to address pivotal questions of building brain functional coordinate system and masking brain activity at the AI-neuroscience interface, and setting a potentially new paradigm in brain activity analysis through downstream adaptation.

A Decomposition-Based Hybrid Ensemble CNN Framework for Improving Cross-Subject EEG Decoding Performance

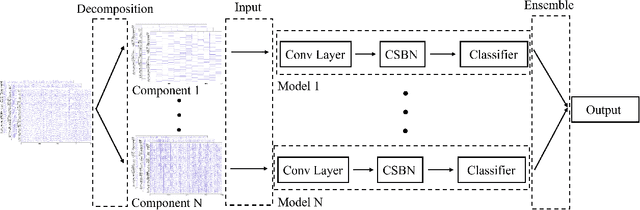
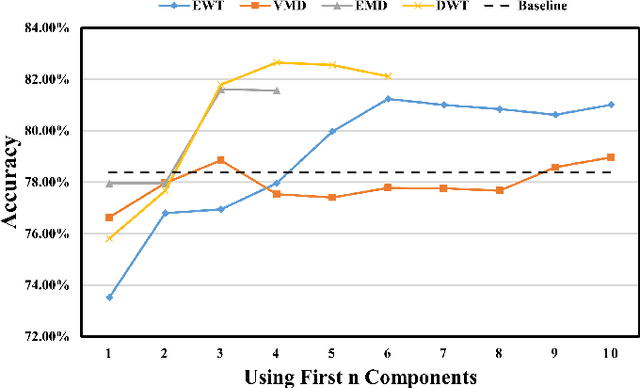
Electroencephalogram (EEG) signals are complex, non-linear, and non-stationary in nature. However, previous studies that applied decomposition to minimize the complexity mainly exploited the hand-engineering features, limiting the information learned in EEG decoding. Therefore, extracting additional primary features from different disassembled components to improve the EEG-based recognition performance remains challenging. On the other hand, attempts have been made to use a single model to learn the hand-engineering features. Less work has been done to improve the generalization ability through ensemble learning. In this work, we propose a novel decomposition-based hybrid ensemble convolutional neural network (CNN) framework to enhance the capability of decoding EEG signals. CNNs, in particular, automatically learn the primary features from raw disassembled components but not handcraft features. The first option is to fuse the obtained score before the Softmax layer and execute back-propagation on the entire ensemble network, whereas the other is to fuse the probability output of the Softmax layer. Moreover, a component-specific batch normalization (CSBN) layer is employed to reduce subject variability. Against the challenging cross-subject driver fatigue-related situation awareness (SA) recognition task, eight models are proposed under the framework, which all showed superior performance than the strong baselines. The performance of different decomposition methods and ensemble modes were further compared. Results indicated that discrete wavelet transform (DWT)-based ensemble CNN achieves the best 82.11% among the proposed models. Our framework can be simply extended to any CNN architecture and applied in any EEG-related sectors, opening the possibility of extracting more preliminary information from complex EEG data.

The Mirror Langevin Algorithm Converges with Vanishing Bias

The technique of modifying the geometry of a problem from Euclidean to Hessian metric has proved to be quite effective in optimization, and has been the subject of study for sampling. The Mirror Langevin Diffusion (MLD) is a sampling analogue of mirror flow in continuous time, and it has nice convergence properties under log-Sobolev or Poincare inequalities relative to the Hessian metric, as shown by Chewi et al. (2020). In discrete time, a simple discretization of MLD is the Mirror Langevin Algorithm (MLA) studied by Zhang et al. (2020), who showed a biased convergence bound with a non-vanishing bias term (does not go to zero as step size goes to zero). This raised the question of whether we need a better analysis or a better discretization to achieve a vanishing bias. Here we study the basic Mirror Langevin Algorithm and show it indeed has a vanishing bias. We apply mean-square analysis based on Li et al. (2019) and Li et al. (2021) to show the mixing time bound for MLA under the modified self-concordance condition introduced by Zhang et al. (2020).

Sqrt(d) Dimension Dependence of Langevin Monte Carlo

This article considers the popular MCMC method of unadjusted Langevin Monte Carlo (LMC) and provides a non-asymptotic analysis of its sampling error in 2-Wasserstein distance. The proof is based on a mean-square analysis framework refined from Li et al. (2019), which works for a large class of sampling algorithms based on discretizations of contractive SDEs. We establish an $\tilde{O}(\sqrt{d}/\epsilon)$ mixing time bound for LMC, without warm start, under the common log-smooth and log-strongly-convex conditions, plus a growth condition on the 3rd-order derivative of the potential of target measures. This bound improves the best previously known $\tilde{O}(d/\epsilon)$ result and is optimal (in terms of order) in both dimension $d$ and accuracy tolerance $\epsilon$ for target measures satisfying the aforementioned assumptions. Our theoretical analysis is further validated by numerical experiments.

A Compact and Interpretable Convolutional Neural Network for Cross-Subject Driver Drowsiness Detection from Single-Channel EEG

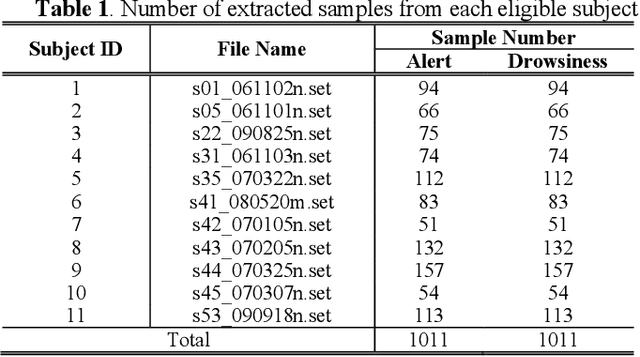
Driver drowsiness is one of main factors leading to road fatalities and hazards in the transportation industry. Electroencephalography (EEG) has been considered as one of the best physiological signals to detect drivers drowsy states, since it directly measures neurophysiological activities in the brain. However, designing a calibration-free system for driver drowsiness detection with EEG is still a challenging task, as EEG suffers from serious mental and physical drifts across different subjects. In this paper, we propose a compact and interpretable Convolutional Neural Network (CNN) to discover shared EEG features across different subjects for driver drowsiness detection. We incorporate the Global Average Pooling (GAP) layer in the model structure, allowing the Class Activation Map (CAM) method to be used for localizing regions of the input signal that contribute most for classification. Results show that the proposed model can achieve an average accuracy of 73.22% on 11 subjects for 2-class cross-subject EEG signal classification, which is higher than conventional machine learning methods and other state-of-art deep learning methods. It is revealed by the visualization technique that the model has learned biologically explainable features, e.g., Alpha spindles and Theta burst, as evidence for the drowsy state. It is also interesting to see that the model uses artifacts that usually dominate the wakeful EEG, e.g., muscle artifacts and sensor drifts, to recognize the alert state. The proposed model illustrates a potential direction to use CNN models as a powerful tool to discover shared features related to different mental states across different subjects from EEG signals.

Hessian-Free High-Resolution Nesterov Acceleration for Sampling

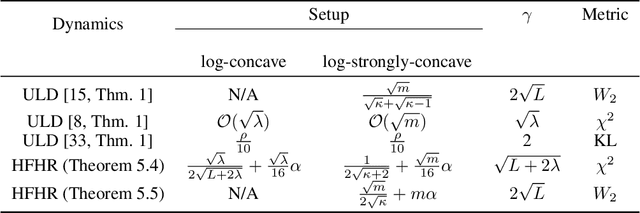
We propose an accelerated-gradient-based MCMC method. It relies on a modification of the Nesterov's accelerated gradient method for strongly convex functions (NAG-SC): We first reformulate NAG-SC as a Hessian-Free High-Resolution ODE, then release the high-resolution coefficient as a free hyperparameter, and finally inject appropriate noise and discretize the diffusion process. Accelerated sampling enabled by this new hyperparameter is not only experimentally demonstrated on several learning tasks, but also theoretically quantified, both at the continuous level and after discretization. For (not-necessarily-strongly-) convex and $L$-smooth potentials, exponential convergence in $\chi^2$ divergence is proved, with a rate analogous to state-of-the-art results of underdamped Langevin dynamics, plus an additional acceleration. At the same time, the method also works for nonconvex potentials, for which we also establish exponential convergence as long as the potential satisfies a Poincar\'e inequality.

Improving Sampling Accuracy of Stochastic Gradient MCMC Methods via Non-uniform Subsampling of Gradients

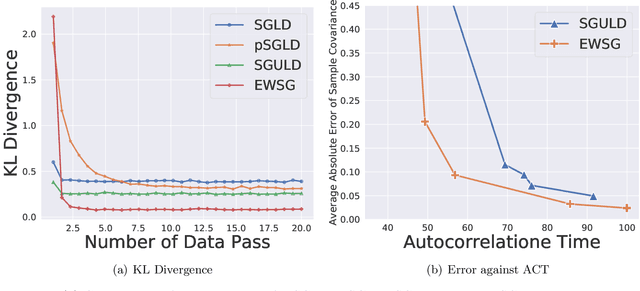
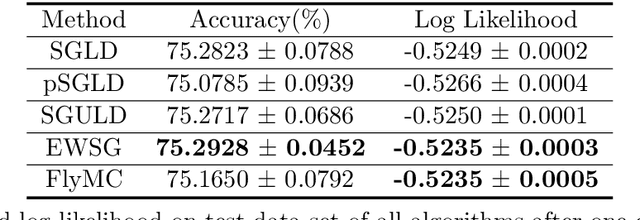
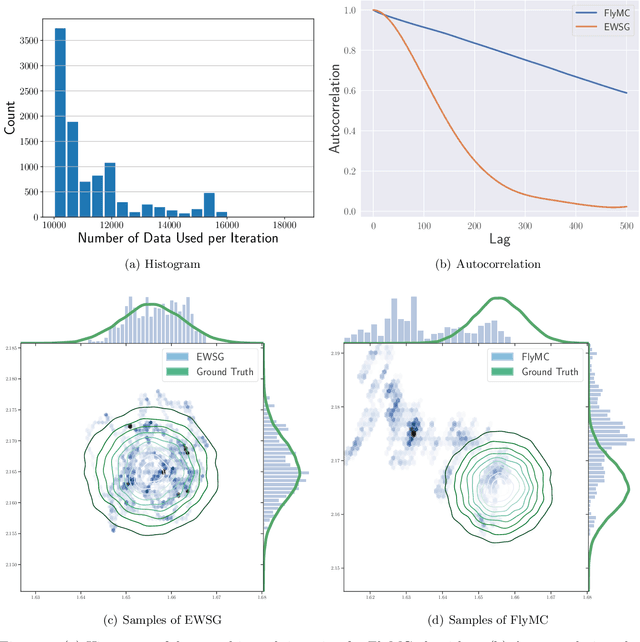
Common Stochastic Gradient MCMC methods approximate gradients by stochastic ones via uniformly subsampled data points. We propose that a non-uniform subsampling can reduce the variance introduced by the stochastic approximation, hence making the sampling of a target distribution more accurate. An exponentially weighted stochastic gradient approach (EWSG) is developed for this objective by matching the transition kernels of SG-MCMC methods respectively based on stochastic and batch gradients. A demonstration of EWSG combined with second-order Langevin equation for sampling purposes is provided. In our method, non-uniform subsampling is done efficiently via a Metropolis-Hasting chain on the data index, which is coupled to the sampling algorithm. The fact that our method has reduced local variance with high probability is theoretically analyzed. A non-asymptotic global error analysis is also presented. Numerical experiments based on both synthetic and real world data sets are also provided to demonstrate the efficacy of the proposed approaches. While statistical accuracy has improved, the speed of convergence was empirically observed to be at least comparable to the uniform version.

A cost-reducing partial labeling estimator in text classification problem

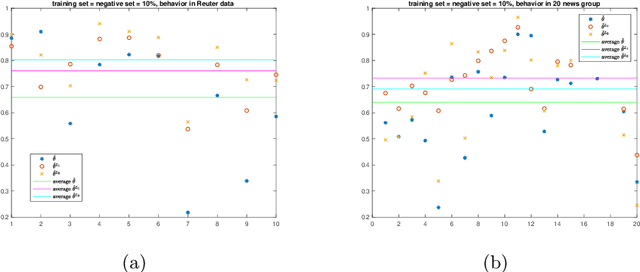
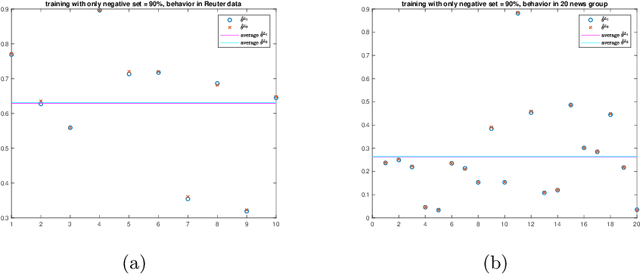
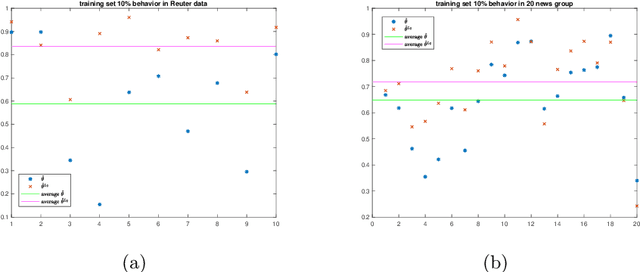
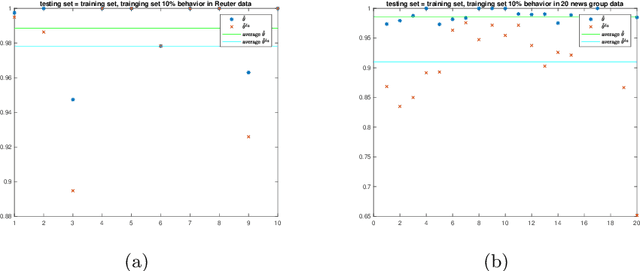
We propose a new approach to address the text classification problems when learning with partial labels is beneficial. Instead of offering each training sample a set of candidate labels, we assign negative-oriented labels to the ambiguous training examples if they are unlikely fall into certain classes. We construct our new maximum likelihood estimators with self-correction property, and prove that under some conditions, our estimators converge faster. Also we discuss the advantages of applying one of our estimator to a fully supervised learning problem. The proposed method has potential applicability in many areas, such as crowdsourcing, natural language processing and medical image analysis.

Learning to Match via Inverse Optimal Transport

We propose a unified data-driven framework based on inverse optimal transport that can learn adaptive, nonlinear interaction cost function from noisy and incomplete empirical matching matrix and predict new matching in various matching contexts. We emphasize that the discrete optimal transport plays the role of a variational principle which gives rise to an optimization-based framework for modeling the observed empirical matching data. Our formulation leads to a non-convex optimization problem which can be solved efficiently by an alternating optimization method. A key novel aspect of our formulation is the incorporation of marginal relaxation via regularized Wasserstein distance, significantly improving the robustness of the method in the face of noisy or missing empirical matching data. Our model falls into the category of prescriptive models, which not only predict potential future matching, but is also able to explain what leads to empirical matching and quantifies the impact of changes in matching factors. The proposed approach has wide applicability including predicting matching in online dating, labor market, college application and crowdsourcing. We back up our claims with numerical experiments on both synthetic data and real world data sets.

Efficient fetal-maternal ECG signal separation from two channel maternal abdominal ECG via diffusion-based channel selection

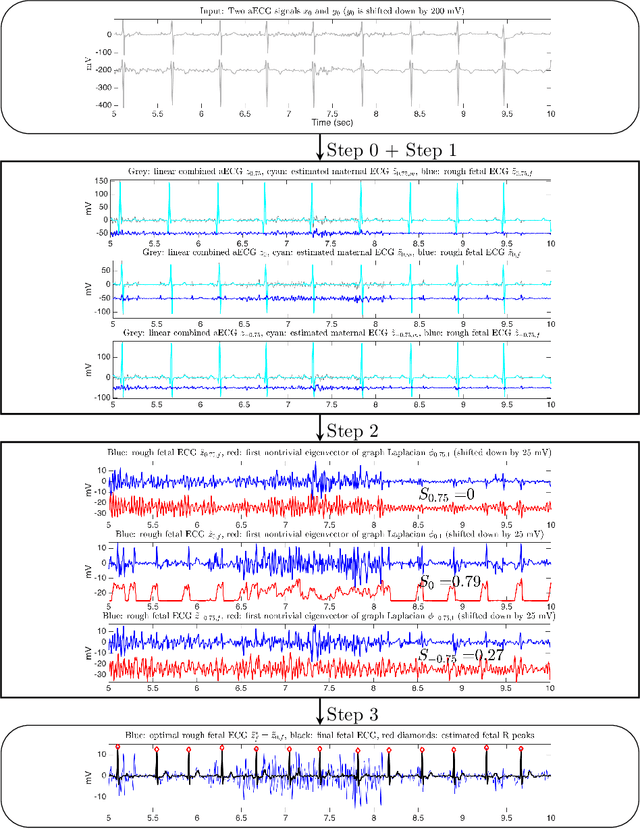
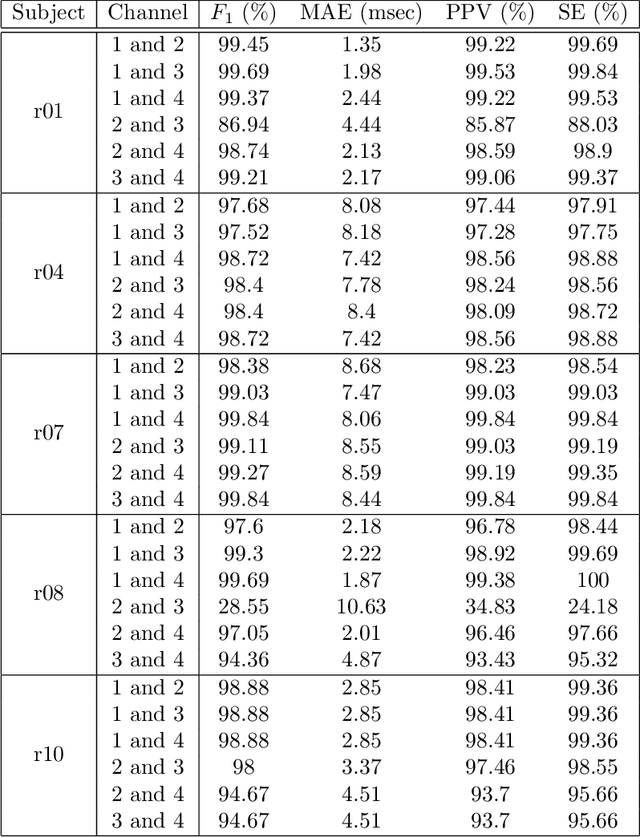
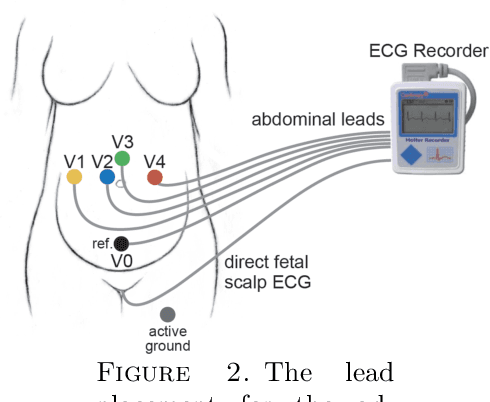
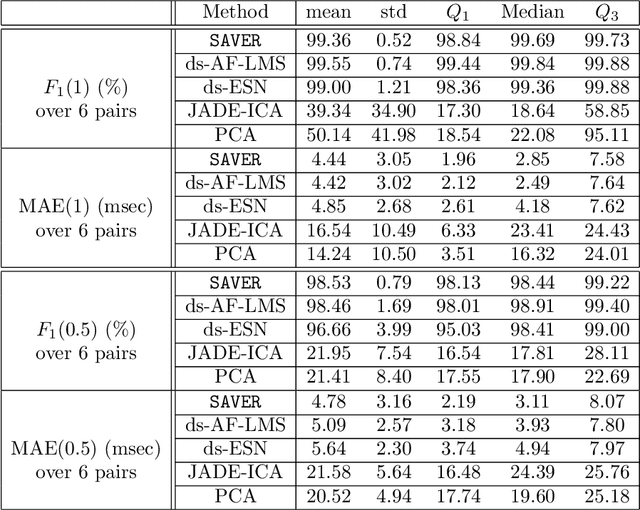
There is a need for affordable, widely deployable maternal-fetal ECG monitors to improve maternal and fetal health during pregnancy and delivery. Based on the diffusion-based channel selection, here we present the mathematical formalism and clinical validation of an algorithm capable of accurate separation of maternal and fetal ECG from a two channel signal acquired over maternal abdomen.