Hessian-Free High-Resolution Nesterov Acceleration for Sampling

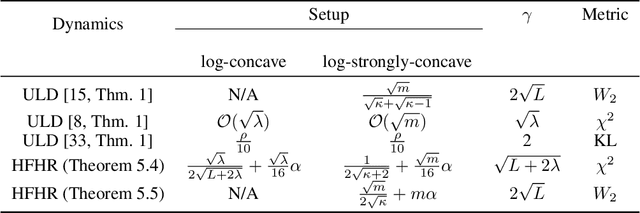
We propose an accelerated-gradient-based MCMC method. It relies on a modification of the Nesterov's accelerated gradient method for strongly convex functions (NAG-SC): We first reformulate NAG-SC as a Hessian-Free High-Resolution ODE, then release the high-resolution coefficient as a free hyperparameter, and finally inject appropriate noise and discretize the diffusion process. Accelerated sampling enabled by this new hyperparameter is not only experimentally demonstrated on several learning tasks, but also theoretically quantified, both at the continuous level and after discretization. For (not-necessarily-strongly-) convex and $L$-smooth potentials, exponential convergence in $\chi^2$ divergence is proved, with a rate analogous to state-of-the-art results of underdamped Langevin dynamics, plus an additional acceleration. At the same time, the method also works for nonconvex potentials, for which we also establish exponential convergence as long as the potential satisfies a Poincar\'e inequality.