Molei Tao
From Masks to Worlds: A Hitchhiker's Guide to World Models
Oct 23, 2025Abstract:This is not a typical survey of world models; it is a guide for those who want to build worlds. We do not aim to catalog every paper that has ever mentioned a ``world model". Instead, we follow one clear road: from early masked models that unified representation learning across modalities, to unified architectures that share a single paradigm, then to interactive generative models that close the action-perception loop, and finally to memory-augmented systems that sustain consistent worlds over time. We bypass loosely related branches to focus on the core: the generative heart, the interactive loop, and the memory system. We show that this is the most promising path towards true world models.
Variational Learning Finds Flatter Solutions at the Edge of Stability
Jun 15, 2025Abstract:Variational Learning (VL) has recently gained popularity for training deep neural networks and is competitive to standard learning methods. Part of its empirical success can be explained by theories such as PAC-Bayes bounds, minimum description length and marginal likelihood, but there are few tools to unravel the implicit regularization in play. Here, we analyze the implicit regularization of VL through the Edge of Stability (EoS) framework. EoS has previously been used to show that gradient descent can find flat solutions and we extend this result to VL to show that it can find even flatter solutions. This is obtained by controlling the posterior covariance and the number of Monte Carlo samples from the posterior. These results are derived in a similar fashion as the standard EoS literature for deep learning, by first deriving a result for a quadratic problem and then extending it to deep neural networks. We empirically validate these findings on a wide variety of large networks, such as ResNet and ViT, to find that the theoretical results closely match the empirical ones. Ours is the first work to analyze the EoS dynamics in VL.
Diffuse Everything: Multimodal Diffusion Models on Arbitrary State Spaces
Jun 09, 2025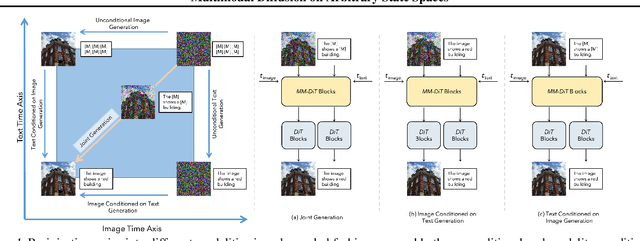
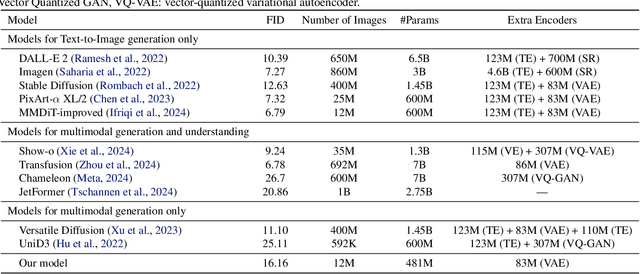
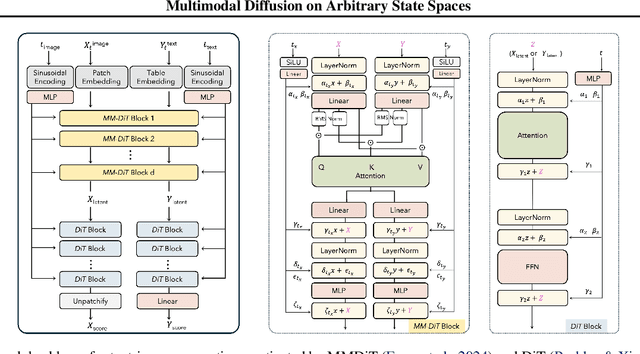
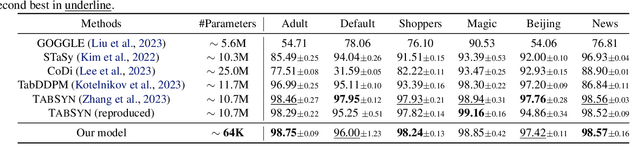
Abstract:Diffusion models have demonstrated remarkable performance in generating unimodal data across various tasks, including image, video, and text generation. On the contrary, the joint generation of multimodal data through diffusion models is still in the early stages of exploration. Existing approaches heavily rely on external preprocessing protocols, such as tokenizers and variational autoencoders, to harmonize varied data representations into a unified, unimodal format. This process heavily demands the high accuracy of encoders and decoders, which can be problematic for applications with limited data. To lift this restriction, we propose a novel framework for building multimodal diffusion models on arbitrary state spaces, enabling native generation of coupled data across different modalities. By introducing an innovative decoupled noise schedule for each modality, we enable both unconditional and modality-conditioned generation within a single model simultaneously. We empirically validate our approach for text-image generation and mixed-type tabular data synthesis, demonstrating that it achieves competitive performance.
Complexity Analysis of Normalizing Constant Estimation: from Jarzynski Equality to Annealed Importance Sampling and beyond
Feb 07, 2025Abstract:Given an unnormalized probability density $\pi\propto\mathrm{e}^{-V}$, estimating its normalizing constant $Z=\int_{\mathbb{R}^d}\mathrm{e}^{-V(x)}\mathrm{d}x$ or free energy $F=-\log Z$ is a crucial problem in Bayesian statistics, statistical mechanics, and machine learning. It is challenging especially in high dimensions or when $\pi$ is multimodal. To mitigate the high variance of conventional importance sampling estimators, annealing-based methods such as Jarzynski equality and annealed importance sampling are commonly adopted, yet their quantitative complexity guarantees remain largely unexplored. We take a first step toward a non-asymptotic analysis of annealed importance sampling. In particular, we derive an oracle complexity of $\widetilde{O}\left(\frac{d\beta^2{\mathcal{A}}^2}{\varepsilon^4}\right)$ for estimating $Z$ within $\varepsilon$ relative error with high probability, where $\beta$ is the smoothness of $V$ and $\mathcal{A}$ denotes the action of a curve of probability measures interpolating $\pi$ and a tractable reference distribution. Our analysis, leveraging Girsanov theorem and optimal transport, does not explicitly require isoperimetric assumptions on the target distribution. Finally, to tackle the large action of the widely used geometric interpolation of probability distributions, we propose a new normalizing constant estimation algorithm based on reverse diffusion samplers and establish a framework for analyzing its complexity.
Variational Schrödinger Momentum Diffusion
Jan 28, 2025



Abstract:The momentum Schr\"odinger Bridge (mSB) has emerged as a leading method for accelerating generative diffusion processes and reducing transport costs. However, the lack of simulation-free properties inevitably results in high training costs and affects scalability. To obtain a trade-off between transport properties and scalability, we introduce variational Schr\"odinger momentum diffusion (VSMD), which employs linearized forward score functions (variational scores) to eliminate the dependence on simulated forward trajectories. Our approach leverages a multivariate diffusion process with adaptively transport-optimized variational scores. Additionally, we apply a critical-damping transform to stabilize training by removing the need for score estimations for both velocity and samples. Theoretically, we prove the convergence of samples generated with optimal variational scores and momentum diffusion. Empirical results demonstrate that VSMD efficiently generates anisotropic shapes while maintaining transport efficacy, outperforming overdamped alternatives, and avoiding complex denoising processes. Our approach also scales effectively to real-world data, achieving competitive results in time series and image generation.
Diffusion Generative Modeling for Spatially Resolved Gene Expression Inference from Histology Images
Jan 26, 2025



Abstract:Spatial Transcriptomics (ST) allows a high-resolution measurement of RNA sequence abundance by systematically connecting cell morphology depicted in Hematoxylin and Eosin (H&E) stained histology images to spatially resolved gene expressions. ST is a time-consuming, expensive yet powerful experimental technique that provides new opportunities to understand cancer mechanisms at a fine-grained molecular level, which is critical for uncovering new approaches for disease diagnosis and treatments. Here, we present $\textbf{Stem}$ ($\textbf{S}$pa$\textbf{T}$ially resolved gene $\textbf{E}$xpression inference with diffusion $\textbf{M}$odel), a novel computational tool that leverages a conditional diffusion generative model to enable in silico gene expression inference from H&E stained images. Through better capturing the inherent stochasticity and heterogeneity in ST data, $\textbf{Stem}$ achieves state-of-the-art performance on spatial gene expression prediction and generates biologically meaningful gene profiles for new H&E stained images at test time. We evaluate the proposed algorithm on datasets with various tissue sources and sequencing platforms, where it demonstrates clear improvement over existing approaches. $\textbf{Stem}$ generates high-fidelity gene expression predictions that share similar gene variation levels as ground truth data, suggesting that our method preserves the underlying biological heterogeneity. Our proposed pipeline opens up the possibility of analyzing existing, easily accessible H&E stained histology images from a genomics point of view without physically performing gene expression profiling and empowers potential biological discovery from H&E stained histology images.
Generative modeling assisted simulation of measurement-altered quantum criticality
Dec 02, 2024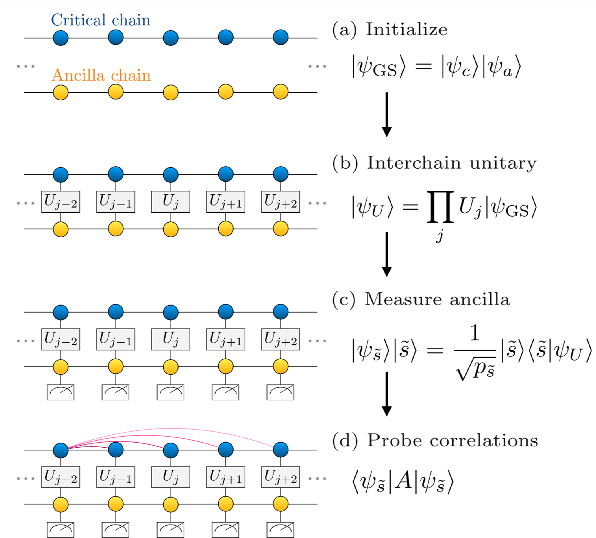
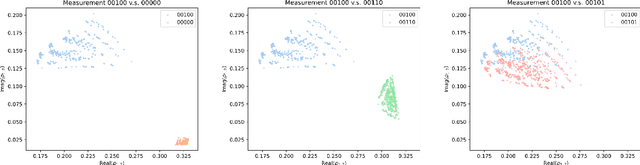
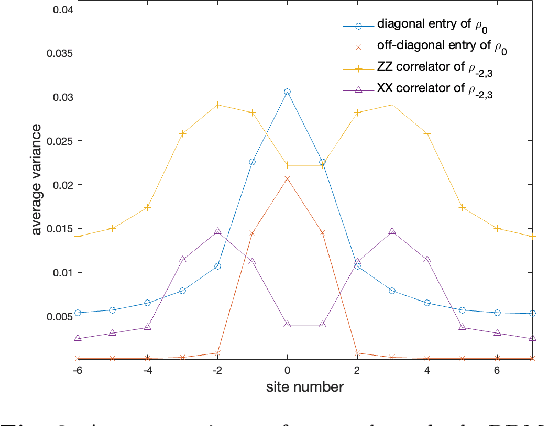
Abstract:In quantum many-body systems, measurements can induce qualitative new features, but their simulation is hindered by the exponential complexity involved in sampling the measurement results. We propose to use machine learning to assist the simulation of measurement-induced quantum phenomena. In particular, we focus on the measurement-altered quantum criticality protocol and generate local reduced density matrices of the critical chain given random measurement results. Such generation is enabled by a physics-preserving conditional diffusion generative model, which learns an observation-indexed probability distribution of an ensemble of quantum states, and then samples from that distribution given an observation.
Provable Acceleration of Nesterov's Accelerated Gradient for Rectangular Matrix Factorization and Linear Neural Networks
Oct 12, 2024



Abstract:We study the convergence rate of first-order methods for rectangular matrix factorization, which is a canonical nonconvex optimization problem. Specifically, given a rank-$r$ matrix $\mathbf{A}\in\mathbb{R}^{m\times n}$, we prove that gradient descent (GD) can find a pair of $\epsilon$-optimal solutions $\mathbf{X}_T\in\mathbb{R}^{m\times d}$ and $\mathbf{Y}_T\in\mathbb{R}^{n\times d}$, where $d\geq r$, satisfying $\lVert\mathbf{X}_T\mathbf{Y}_T^\top-\mathbf{A}\rVert_\mathrm{F}\leq\epsilon\lVert\mathbf{A}\rVert_\mathrm{F}$ in $T=O(\kappa^2\log\frac{1}{\epsilon})$ iterations with high probability, where $\kappa$ denotes the condition number of $\mathbf{A}$. Furthermore, we prove that Nesterov's accelerated gradient (NAG) attains an iteration complexity of $O(\kappa\log\frac{1}{\epsilon})$, which is the best-known bound of first-order methods for rectangular matrix factorization. Different from small balanced random initialization in the existing literature, we adopt an unbalanced initialization, where $\mathbf{X}_0$ is large and $\mathbf{Y}_0$ is $0$. Moreover, our initialization and analysis can be further extended to linear neural networks, where we prove that NAG can also attain an accelerated linear convergence rate. In particular, we only require the width of the network to be greater than or equal to the rank of the output label matrix. In contrast, previous results achieving the same rate require excessive widths that additionally depend on the condition number and the rank of the input data matrix.
Plug-and-Play Controllable Generation for Discrete Masked Models
Oct 03, 2024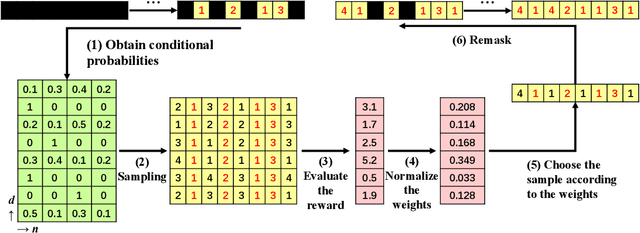
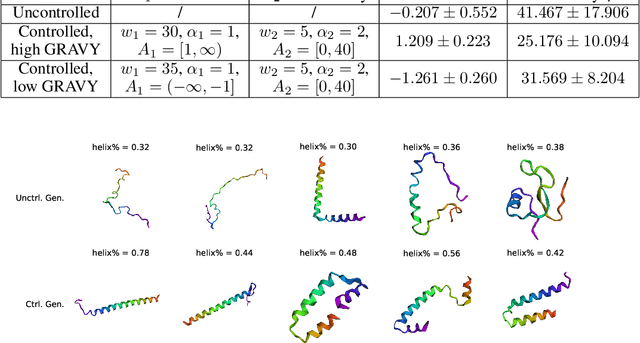
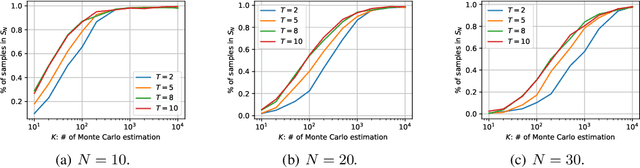
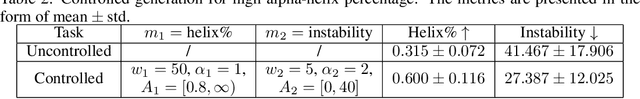
Abstract:This article makes discrete masked models for the generative modeling of discrete data controllable. The goal is to generate samples of a discrete random variable that adheres to a posterior distribution, satisfies specific constraints, or optimizes a reward function. This methodological development enables broad applications across downstream tasks such as class-specific image generation and protein design. Existing approaches for controllable generation of masked models typically rely on task-specific fine-tuning or additional modifications, which can be inefficient and resource-intensive. To overcome these limitations, we propose a novel plug-and-play framework based on importance sampling that bypasses the need for training a conditional score. Our framework is agnostic to the choice of control criteria, requires no gradient information, and is well-suited for tasks such as posterior sampling, Bayesian inverse problems, and constrained generation. We demonstrate the effectiveness of our approach through extensive experiments, showcasing its versatility across multiple domains, including protein design.
DeepTTV: Deep Learning Prediction of Hidden Exoplanet From Transit Timing Variations
Sep 06, 2024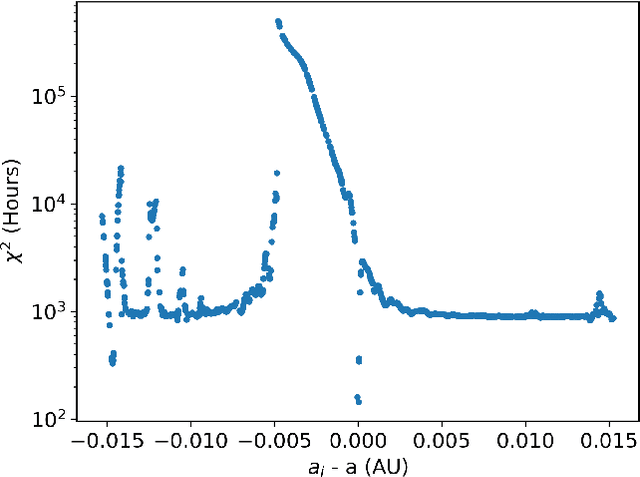
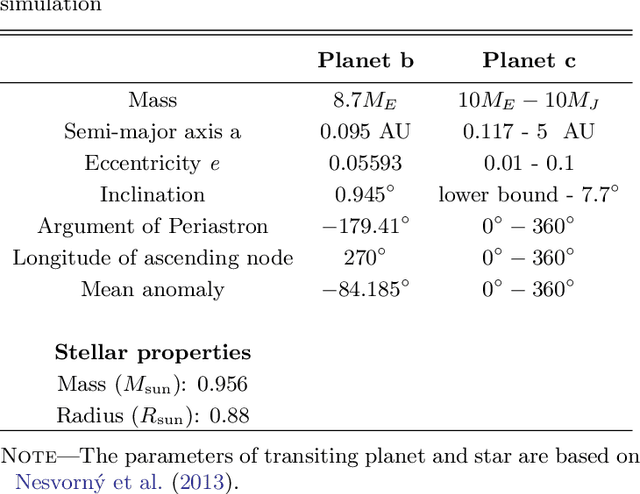
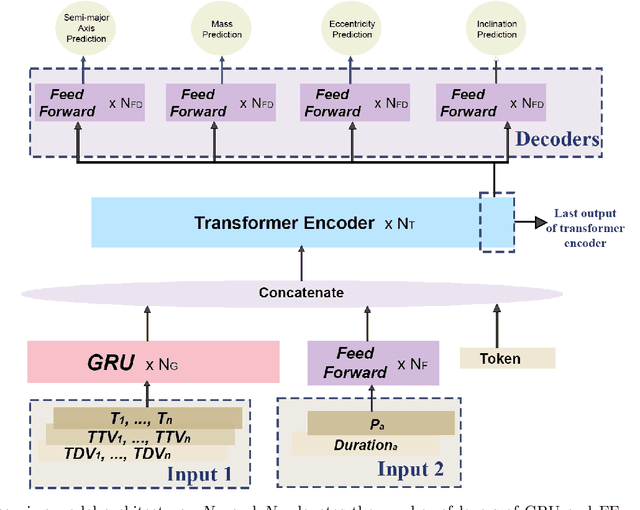
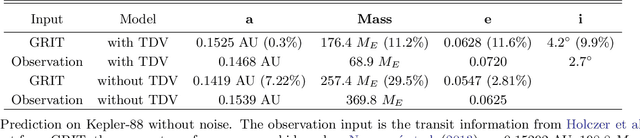
Abstract:Transit timing variation (TTV) provides rich information about the mass and orbital properties of exoplanets, which are often obtained by solving an inverse problem via Markov Chain Monte Carlo (MCMC). In this paper, we design a new data-driven approach, which potentially can be applied to problems that are hard to traditional MCMC methods, such as the case with only one planet transiting. Specifically, we use a deep learning approach to predict the parameters of non-transit companion for the single transit system with transit information (i.e., TTV, and Transit Duration Variation (TDV)) as input. Thanks to a newly constructed \textit{Transformer}-based architecture that can extract long-range interactions from TTV sequential data, this previously difficult task can now be accomplished with high accuracy, with an overall fractional error of $\sim$2\% on mass and eccentricity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge