COSMOS: A Hybrid Adaptive Optimizer for Memory-Efficient Training of LLMs

Large Language Models (LLMs) have demonstrated remarkable success across various domains, yet their optimization remains a significant challenge due to the complex and high-dimensional loss landscapes they inhabit. While adaptive optimizers such as AdamW are widely used, they suffer from critical limitations, including an inability to capture interdependencies between coordinates and high memory consumption. Subsequent research, exemplified by SOAP, attempts to better capture coordinate interdependence but incurs greater memory overhead, limiting scalability for massive LLMs. An alternative approach aims to reduce memory consumption through low-dimensional projection, but this leads to substantial approximation errors, resulting in less effective optimization (e.g., in terms of per-token efficiency). In this paper, we propose COSMOS, a novel hybrid optimizer that leverages the varying importance of eigensubspaces in the gradient matrix to achieve memory efficiency without compromising optimization performance. The design of COSMOS is motivated by our empirical insights and practical considerations. Specifically, COSMOS applies SOAP to the leading eigensubspace, which captures the primary optimization dynamics, and MUON to the remaining eigensubspace, which is less critical but computationally expensive to handle with SOAP. This hybrid strategy significantly reduces memory consumption while maintaining robust optimization performance, making it particularly suitable for massive LLMs. Numerical experiments on various datasets and transformer architectures are provided to demonstrate the effectiveness of COSMOS. Our code is available at https://github.com/lliu606/COSMOS.

Provable Acceleration of Nesterov's Accelerated Gradient for Rectangular Matrix Factorization and Linear Neural Networks

We study the convergence rate of first-order methods for rectangular matrix factorization, which is a canonical nonconvex optimization problem. Specifically, given a rank-$r$ matrix $\mathbf{A}\in\mathbb{R}^{m\times n}$, we prove that gradient descent (GD) can find a pair of $\epsilon$-optimal solutions $\mathbf{X}_T\in\mathbb{R}^{m\times d}$ and $\mathbf{Y}_T\in\mathbb{R}^{n\times d}$, where $d\geq r$, satisfying $\lVert\mathbf{X}_T\mathbf{Y}_T^\top-\mathbf{A}\rVert_\mathrm{F}\leq\epsilon\lVert\mathbf{A}\rVert_\mathrm{F}$ in $T=O(\kappa^2\log\frac{1}{\epsilon})$ iterations with high probability, where $\kappa$ denotes the condition number of $\mathbf{A}$. Furthermore, we prove that Nesterov's accelerated gradient (NAG) attains an iteration complexity of $O(\kappa\log\frac{1}{\epsilon})$, which is the best-known bound of first-order methods for rectangular matrix factorization. Different from small balanced random initialization in the existing literature, we adopt an unbalanced initialization, where $\mathbf{X}_0$ is large and $\mathbf{Y}_0$ is $0$. Moreover, our initialization and analysis can be further extended to linear neural networks, where we prove that NAG can also attain an accelerated linear convergence rate. In particular, we only require the width of the network to be greater than or equal to the rank of the output label matrix. In contrast, previous results achieving the same rate require excessive widths that additionally depend on the condition number and the rank of the input data matrix.

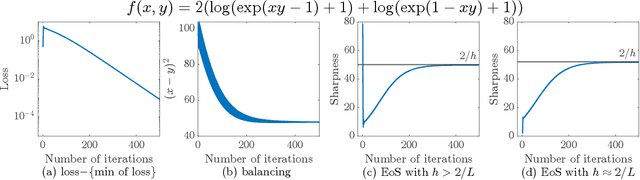
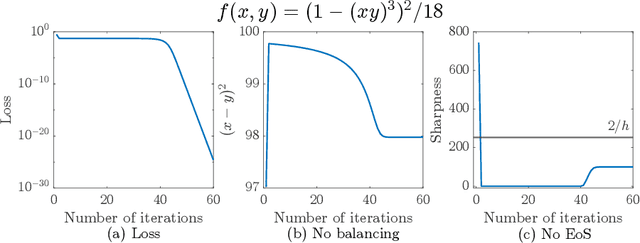
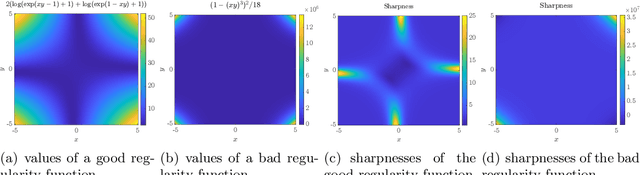
Good regularity creates large learning rate implicit biases: edge of stability, balancing, and catapult

Large learning rates, when applied to gradient descent for nonconvex optimization, yield various implicit biases including the edge of stability (Cohen et al., 2021), balancing (Wang et al., 2022), and catapult (Lewkowycz et al., 2020). These phenomena cannot be well explained by classical optimization theory. Though significant theoretical progress has been made in understanding these implicit biases, it remains unclear for which objective functions would they occur. This paper provides an initial step in answering this question, namely that these implicit biases are in fact various tips of the same iceberg. They occur when the objective function of optimization has some good regularity, which, in combination with a provable preference of large learning rate gradient descent for moving toward flatter regions, results in these nontrivial dynamical phenomena. To establish this result, we develop a new global convergence theory under large learning rates, for a family of nonconvex functions without globally Lipschitz continuous gradient, which was typically assumed in existing convergence analysis. A byproduct is the first non-asymptotic convergence rate bound for large-learning-rate gradient descent optimization of nonconvex functions. We also validate our theory with experiments on neural networks, where different losses, activation functions, and batch normalization all can significantly affect regularity and lead to very different training dynamics.

Score Matching-based Pseudolikelihood Estimation of Neural Marked Spatio-Temporal Point Process with Uncertainty Quantification

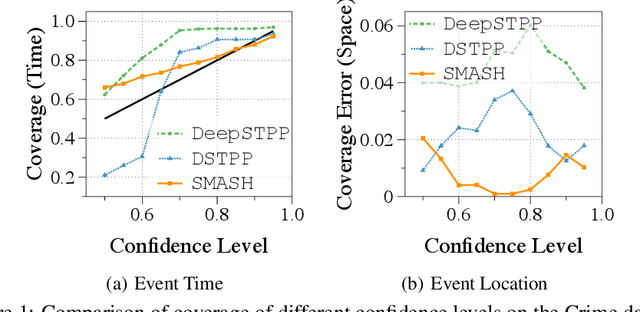
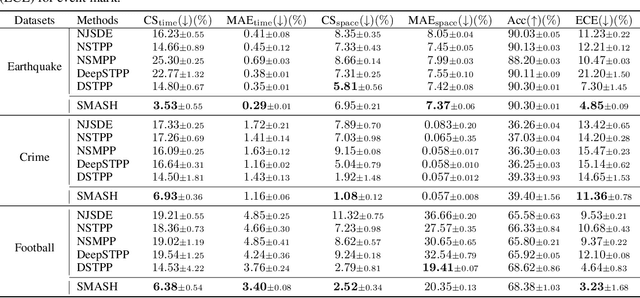
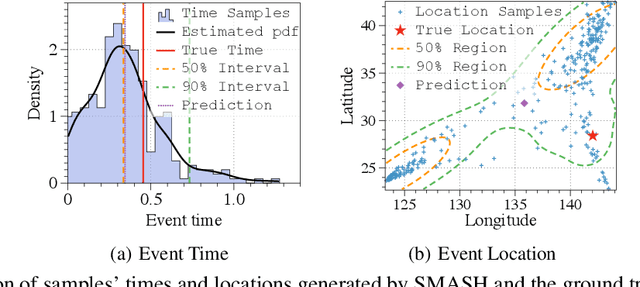
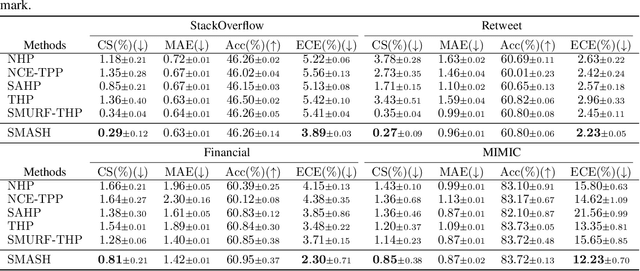
Spatio-temporal point processes (STPPs) are potent mathematical tools for modeling and predicting events with both temporal and spatial features. Despite their versatility, most existing methods for learning STPPs either assume a restricted form of the spatio-temporal distribution, or suffer from inaccurate approximations of the intractable integral in the likelihood training objective. These issues typically arise from the normalization term of the probability density function. Moreover, current techniques fail to provide uncertainty quantification for model predictions, such as confidence intervals for the predicted event's arrival time and confidence regions for the event's location, which is crucial given the considerable randomness of the data. To tackle these challenges, we introduce SMASH: a Score MAtching-based pSeudolikeliHood estimator for learning marked STPPs with uncertainty quantification. Specifically, our framework adopts a normalization-free objective by estimating the pseudolikelihood of marked STPPs through score-matching and offers uncertainty quantification for the predicted event time, location and mark by computing confidence regions over the generated samples. The superior performance of our proposed framework is demonstrated through extensive experiments in both event prediction and uncertainty quantification.

Sample Complexity of Neural Policy Mirror Descent for Policy Optimization on Low-Dimensional Manifolds

Policy-based algorithms equipped with deep neural networks have achieved great success in solving high-dimensional policy optimization problems in reinforcement learning. However, current analyses cannot explain why they are resistant to the curse of dimensionality. In this work, we study the sample complexity of the neural policy mirror descent (NPMD) algorithm with convolutional neural networks (CNN) as function approximators. Motivated by the empirical observation that many high-dimensional environments have state spaces possessing low-dimensional structures, such as those taking images as states, we consider the state space to be a $d$-dimensional manifold embedded in the $D$-dimensional Euclidean space with intrinsic dimension $d\ll D$. We show that in each iteration of NPMD, both the value function and the policy can be well approximated by CNNs. The approximation errors are controlled by the size of the networks, and the smoothness of the previous networks can be inherited. As a result, by properly choosing the network size and hyperparameters, NPMD can find an $\epsilon$-optimal policy with $\widetilde{O}(\epsilon^{-\frac{d}{\alpha}-2})$ samples in expectation, where $\alpha\in(0,1]$ indicates the smoothness of environment. Compared to previous work, our result exhibits that NPMD can leverage the low-dimensional structure of state space to escape from the curse of dimensionality, providing an explanation for the efficacy of deep policy-based algorithms.