LLMs Can Generate a Better Answer by Aggregating Their Own Responses

Large Language Models (LLMs) have shown remarkable capabilities across tasks, yet they often require additional prompting techniques when facing complex problems. While approaches like self-correction and response selection have emerged as popular solutions, recent studies have shown these methods perform poorly when relying on the LLM itself to provide feedback or selection criteria. We argue this limitation stems from the fact that common LLM post-training procedures lack explicit supervision for discriminative judgment tasks. In this paper, we propose Generative Self-Aggregation (GSA), a novel prompting method that improves answer quality without requiring the model's discriminative capabilities. GSA first samples multiple diverse responses from the LLM, then aggregates them to obtain an improved solution. Unlike previous approaches, our method does not require the LLM to correct errors or compare response quality; instead, it leverages the model's generative abilities to synthesize a new response based on the context of multiple samples. While GSA shares similarities with the self-consistency (SC) approach for response aggregation, SC requires specific verifiable tokens to enable majority voting. In contrast, our approach is more general and can be applied to open-ended tasks. Empirical evaluation demonstrates that GSA effectively improves response quality across various tasks, including mathematical reasoning, knowledge-based problems, and open-ended generation tasks such as code synthesis and conversational responses.

COSMOS: A Hybrid Adaptive Optimizer for Memory-Efficient Training of LLMs

Large Language Models (LLMs) have demonstrated remarkable success across various domains, yet their optimization remains a significant challenge due to the complex and high-dimensional loss landscapes they inhabit. While adaptive optimizers such as AdamW are widely used, they suffer from critical limitations, including an inability to capture interdependencies between coordinates and high memory consumption. Subsequent research, exemplified by SOAP, attempts to better capture coordinate interdependence but incurs greater memory overhead, limiting scalability for massive LLMs. An alternative approach aims to reduce memory consumption through low-dimensional projection, but this leads to substantial approximation errors, resulting in less effective optimization (e.g., in terms of per-token efficiency). In this paper, we propose COSMOS, a novel hybrid optimizer that leverages the varying importance of eigensubspaces in the gradient matrix to achieve memory efficiency without compromising optimization performance. The design of COSMOS is motivated by our empirical insights and practical considerations. Specifically, COSMOS applies SOAP to the leading eigensubspace, which captures the primary optimization dynamics, and MUON to the remaining eigensubspace, which is less critical but computationally expensive to handle with SOAP. This hybrid strategy significantly reduces memory consumption while maintaining robust optimization performance, making it particularly suitable for massive LLMs. Numerical experiments on various datasets and transformer architectures are provided to demonstrate the effectiveness of COSMOS. Our code is available at https://github.com/lliu606/COSMOS.

Adaptive Preference Scaling for Reinforcement Learning with Human Feedback

Reinforcement learning from human feedback (RLHF) is a prevalent approach to align AI systems with human values by learning rewards from human preference data. Due to various reasons, however, such data typically takes the form of rankings over pairs of trajectory segments, which fails to capture the varying strengths of preferences across different pairs. In this paper, we propose a novel adaptive preference loss, underpinned by distributionally robust optimization (DRO), designed to address this uncertainty in preference strength. By incorporating an adaptive scaling parameter into the loss for each pair, our method increases the flexibility of the reward function. Specifically, it assigns small scaling parameters to pairs with ambiguous preferences, leading to more comparable rewards, and large scaling parameters to those with clear preferences for more distinct rewards. Computationally, our proposed loss function is strictly convex and univariate with respect to each scaling parameter, enabling its efficient optimization through a simple second-order algorithm. Our method is versatile and can be readily adapted to various preference optimization frameworks, including direct preference optimization (DPO). Our experiments with robotic control and natural language generation with large language models (LLMs) show that our method not only improves policy performance but also aligns reward function selection more closely with policy optimization, simplifying the hyperparameter tuning process.

SMURF-THP: Score Matching-based UnceRtainty quantiFication for Transformer Hawkes Process

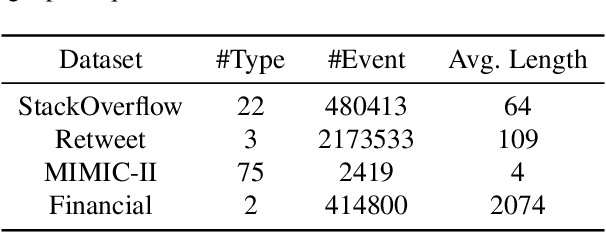
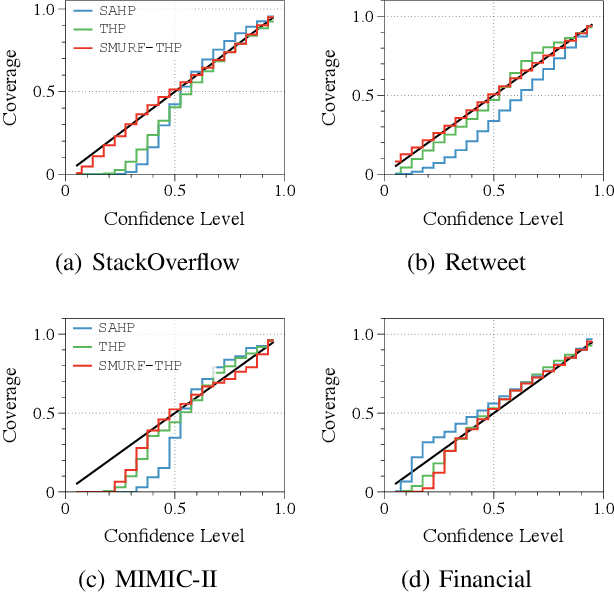
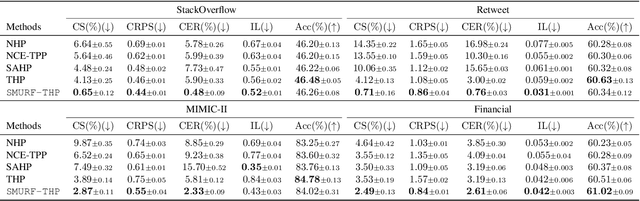
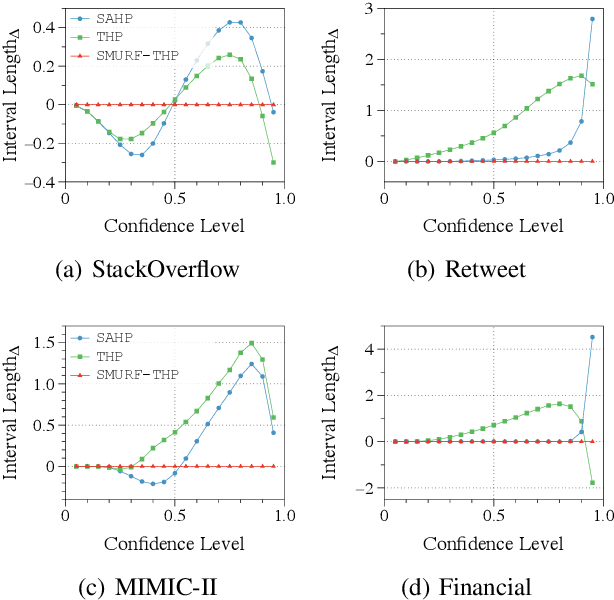
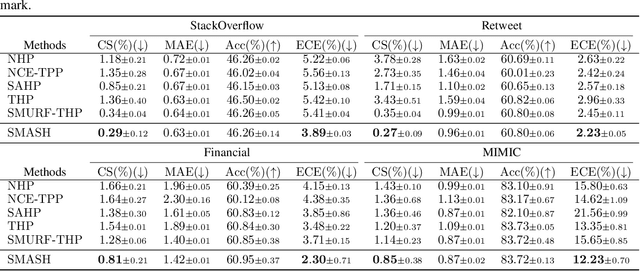
Transformer Hawkes process models have shown to be successful in modeling event sequence data. However, most of the existing training methods rely on maximizing the likelihood of event sequences, which involves calculating some intractable integral. Moreover, the existing methods fail to provide uncertainty quantification for model predictions, e.g., confidence intervals for the predicted event's arrival time. To address these issues, we propose SMURF-THP, a score-based method for learning Transformer Hawkes process and quantifying prediction uncertainty. Specifically, SMURF-THP learns the score function of events' arrival time based on a score-matching objective that avoids the intractable computation. With such a learned score function, we can sample arrival time of events from the predictive distribution. This naturally allows for the quantification of uncertainty by computing confidence intervals over the generated samples. We conduct extensive experiments in both event type prediction and uncertainty quantification of arrival time. In all the experiments, SMURF-THP outperforms existing likelihood-based methods in confidence calibration while exhibiting comparable prediction accuracy.

Score Matching-based Pseudolikelihood Estimation of Neural Marked Spatio-Temporal Point Process with Uncertainty Quantification

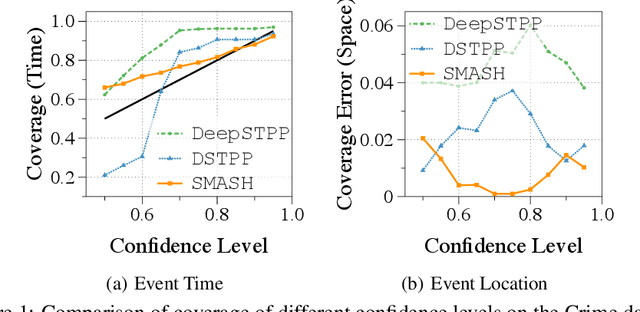
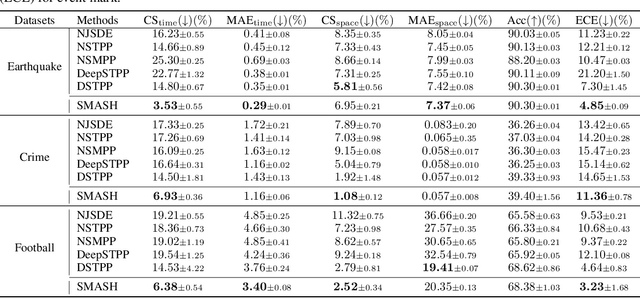
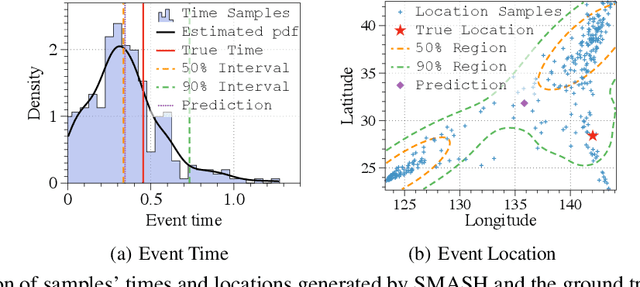
Spatio-temporal point processes (STPPs) are potent mathematical tools for modeling and predicting events with both temporal and spatial features. Despite their versatility, most existing methods for learning STPPs either assume a restricted form of the spatio-temporal distribution, or suffer from inaccurate approximations of the intractable integral in the likelihood training objective. These issues typically arise from the normalization term of the probability density function. Moreover, current techniques fail to provide uncertainty quantification for model predictions, such as confidence intervals for the predicted event's arrival time and confidence regions for the event's location, which is crucial given the considerable randomness of the data. To tackle these challenges, we introduce SMASH: a Score MAtching-based pSeudolikeliHood estimator for learning marked STPPs with uncertainty quantification. Specifically, our framework adopts a normalization-free objective by estimating the pseudolikelihood of marked STPPs through score-matching and offers uncertainty quantification for the predicted event time, location and mark by computing confidence regions over the generated samples. The superior performance of our proposed framework is demonstrated through extensive experiments in both event prediction and uncertainty quantification.

Stochastic Inexact Augmented Lagrangian Method for Nonconvex Expectation Constrained Optimization

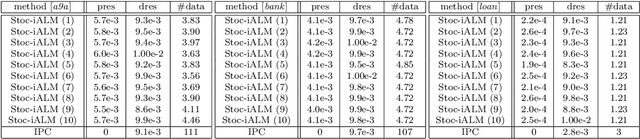
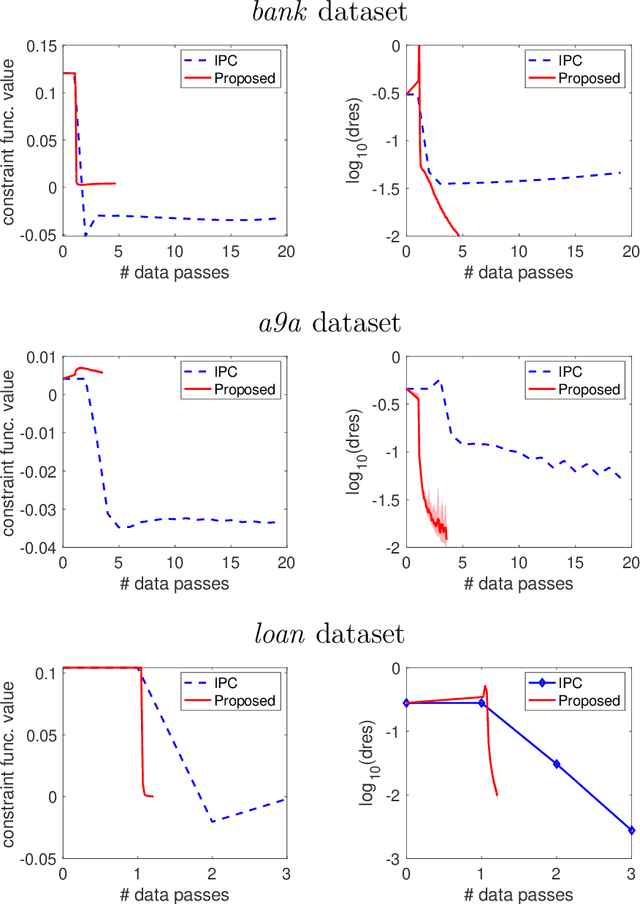
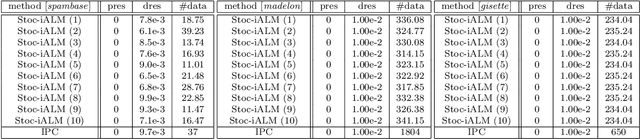
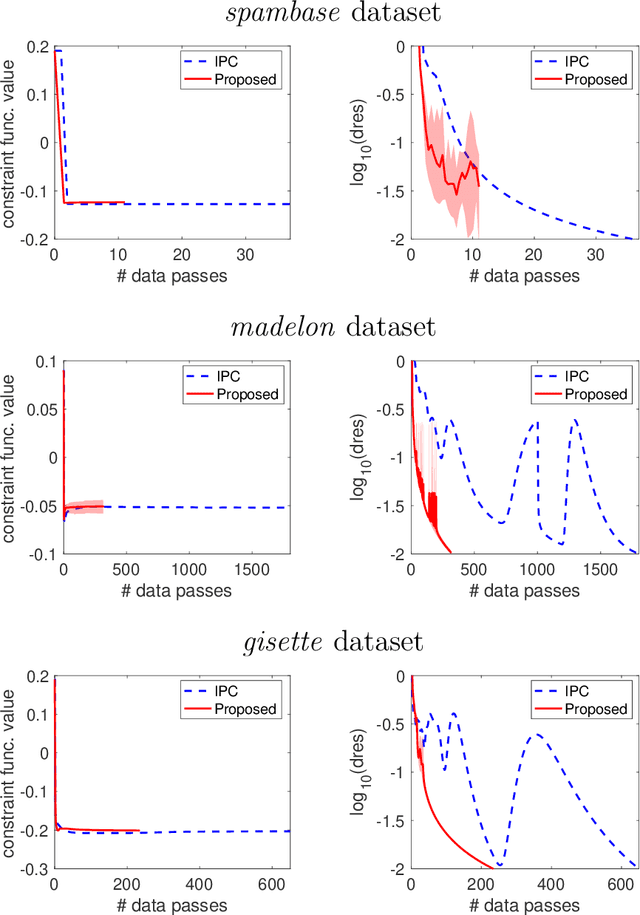
Many real-world problems not only have complicated nonconvex functional constraints but also use a large number of data points. This motivates the design of efficient stochastic methods on finite-sum or expectation constrained problems. In this paper, we design and analyze stochastic inexact augmented Lagrangian methods (Stoc-iALM) to solve problems involving a nonconvex composite (i.e. smooth+nonsmooth) objective and nonconvex smooth functional constraints. We adopt the standard iALM framework and design a subroutine by using the momentum-based variance-reduced proximal stochastic gradient method (PStorm) and a postprocessing step. Under certain regularity conditions (assumed also in existing works), to reach an $\varepsilon$-KKT point in expectation, we establish an oracle complexity result of $O(\varepsilon^{-5})$, which is better than the best-known $O(\varepsilon^{-6})$ result. Numerical experiments on the fairness constrained problem and the Neyman-Pearson classification problem with real data demonstrate that our proposed method outperforms an existing method with the previously best-known complexity result.

Transformer Hawkes Process

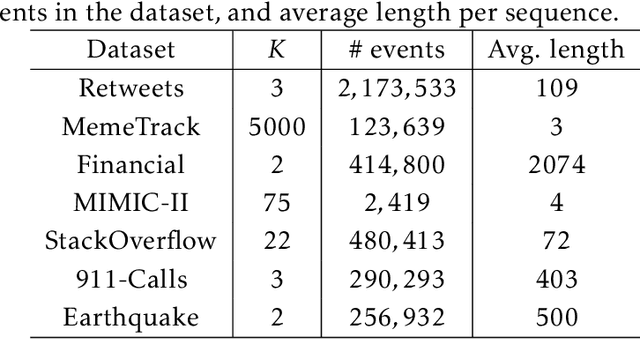
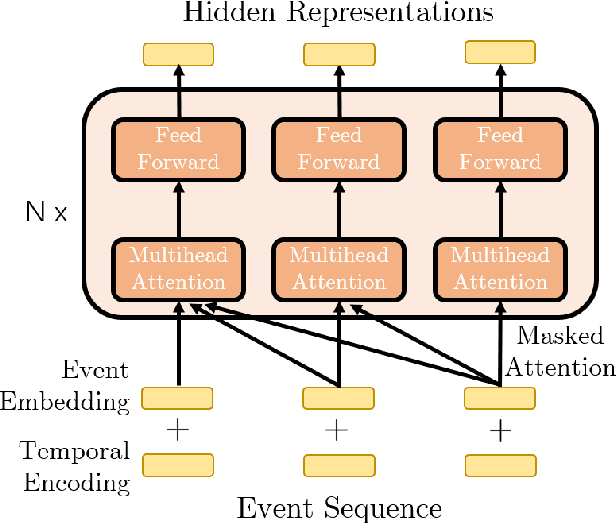
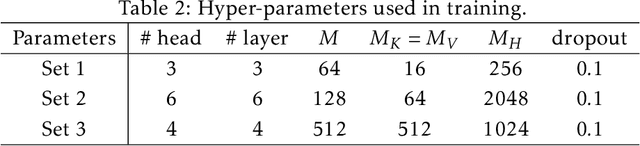
Modern data acquisition routinely produce massive amounts of event sequence data in various domains, such as social media, healthcare, and financial markets. These data often exhibit complicated short-term and long-term temporal dependencies. However, most of the existing recurrent neural network-based point process models fail to capture such dependencies, and yield unreliable prediction performance. To address this issue, we propose a Transformer Hawkes Process (THP) model, which leverages the self-attention mechanism to capture long-term dependencies and meanwhile enjoys computational efficiency. Numerical experiments on various datasets show that THP outperforms existing models in terms of both likelihood and event prediction accuracy by a notable margin. Moreover, THP is quite general and can incorporate additional structural knowledge. We provide a concrete example, where THP achieves improved prediction performance for learning multiple point processes when incorporating their relational information.