Stochastic Inexact Augmented Lagrangian Method for Nonconvex Expectation Constrained Optimization
Paper and Code
Dec 19, 2022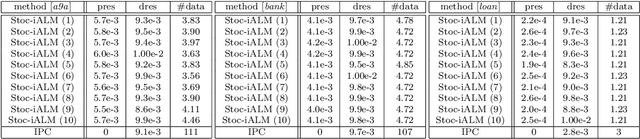
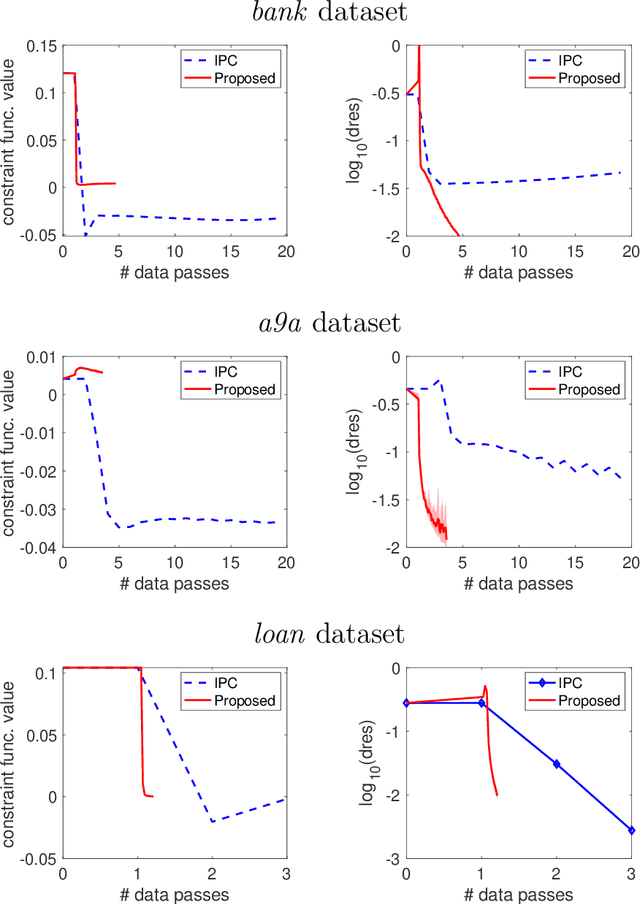
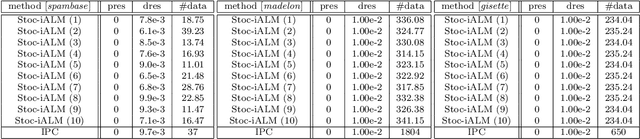
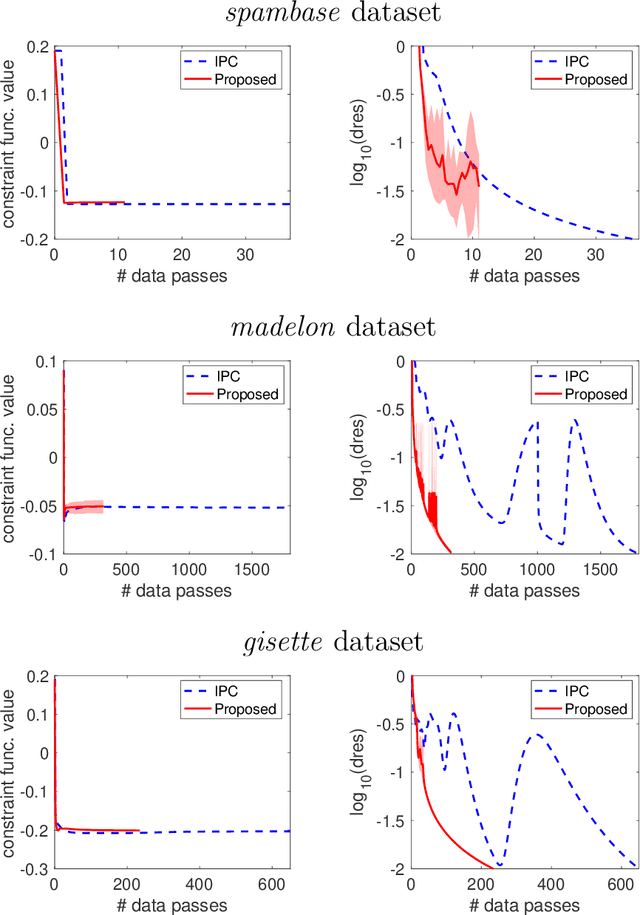
Many real-world problems not only have complicated nonconvex functional constraints but also use a large number of data points. This motivates the design of efficient stochastic methods on finite-sum or expectation constrained problems. In this paper, we design and analyze stochastic inexact augmented Lagrangian methods (Stoc-iALM) to solve problems involving a nonconvex composite (i.e. smooth+nonsmooth) objective and nonconvex smooth functional constraints. We adopt the standard iALM framework and design a subroutine by using the momentum-based variance-reduced proximal stochastic gradient method (PStorm) and a postprocessing step. Under certain regularity conditions (assumed also in existing works), to reach an $\varepsilon$-KKT point in expectation, we establish an oracle complexity result of $O(\varepsilon^{-5})$, which is better than the best-known $O(\varepsilon^{-6})$ result. Numerical experiments on the fairness constrained problem and the Neyman-Pearson classification problem with real data demonstrate that our proposed method outperforms an existing method with the previously best-known complexity result.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge