Score Matching-based Pseudolikelihood Estimation of Neural Marked Spatio-Temporal Point Process with Uncertainty Quantification

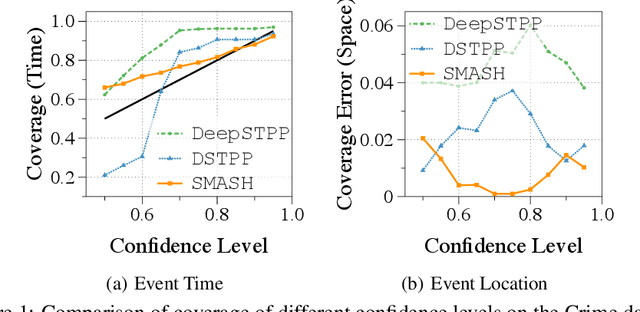
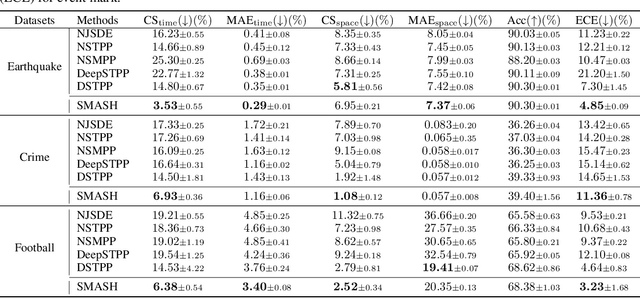
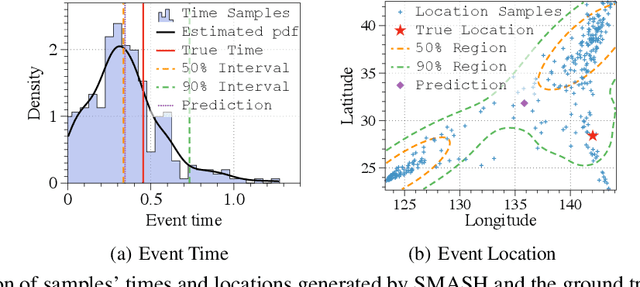
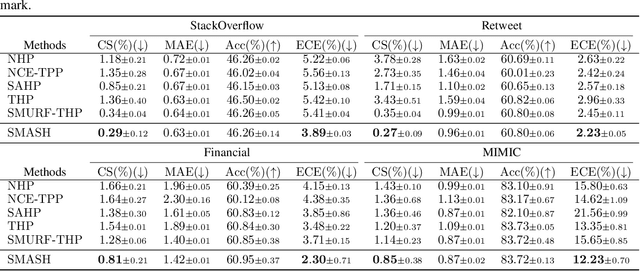
Spatio-temporal point processes (STPPs) are potent mathematical tools for modeling and predicting events with both temporal and spatial features. Despite their versatility, most existing methods for learning STPPs either assume a restricted form of the spatio-temporal distribution, or suffer from inaccurate approximations of the intractable integral in the likelihood training objective. These issues typically arise from the normalization term of the probability density function. Moreover, current techniques fail to provide uncertainty quantification for model predictions, such as confidence intervals for the predicted event's arrival time and confidence regions for the event's location, which is crucial given the considerable randomness of the data. To tackle these challenges, we introduce SMASH: a Score MAtching-based pSeudolikeliHood estimator for learning marked STPPs with uncertainty quantification. Specifically, our framework adopts a normalization-free objective by estimating the pseudolikelihood of marked STPPs through score-matching and offers uncertainty quantification for the predicted event time, location and mark by computing confidence regions over the generated samples. The superior performance of our proposed framework is demonstrated through extensive experiments in both event prediction and uncertainty quantification.

Pivotal Estimation of Linear Discriminant Analysis in High Dimensions

We consider the linear discriminant analysis problem in the high-dimensional settings. In this work, we propose PANDA(PivotAl liNear Discriminant Analysis), a tuning-insensitive method in the sense that it requires very little effort to tune the parameters. Moreover, we prove that PANDA achieves the optimal convergence rate in terms of both the estimation error and misclassification rate. Our theoretical results are backed up by thorough numerical studies using both simulated and real datasets. In comparison with the existing methods, we observe that our proposed PANDA yields equal or better performance, and requires substantially less effort in parameter tuning.

Covariance Estimators for the ROOT-SGD Algorithm in Online Learning

Online learning naturally arises in many statistical and machine learning problems. The most widely used methods in online learning are stochastic first-order algorithms. Among this family of algorithms, there is a recently developed algorithm, Recursive One-Over-T SGD (ROOT-SGD). ROOT-SGD is advantageous in that it converges at a non-asymptotically fast rate, and its estimator further converges to a normal distribution. However, this normal distribution has unknown asymptotic covariance; thus cannot be directly applied to measure the uncertainty. To fill this gap, we develop two estimators for the asymptotic covariance of ROOT-SGD. Our covariance estimators are useful for statistical inference in ROOT-SGD. Our first estimator adopts the idea of plug-in. For each unknown component in the formula of the asymptotic covariance, we substitute it with its empirical counterpart. The plug-in estimator converges at the rate $\mathcal{O}(1/\sqrt{t})$, where $t$ is the sample size. Despite its quick convergence, the plug-in estimator has the limitation that it relies on the Hessian of the loss function, which might be unavailable in some cases. Our second estimator is a Hessian-free estimator that overcomes the aforementioned limitation. The Hessian-free estimator uses the random-scaling technique, and we show that it is an asymptotically consistent estimator of the true covariance.

Adaptive Partially-Observed Sequential Change Detection and Isolation

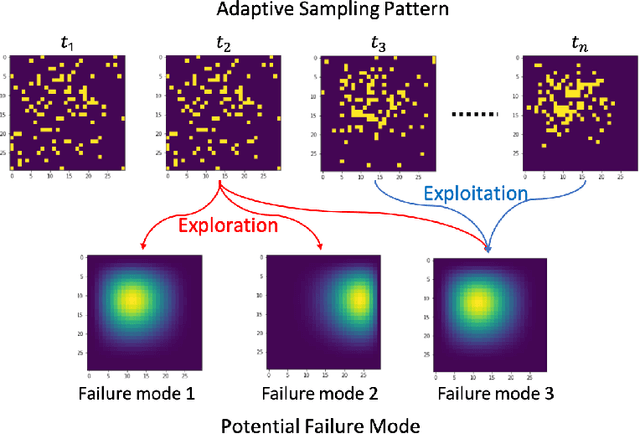
High-dimensional data has become popular due to the easy accessibility of sensors in modern industrial applications. However, one specific challenge is that it is often not easy to obtain complete measurements due to limited sensing powers and resource constraints. Furthermore, distinct failure patterns may exist in the systems, and it is necessary to identify the true failure pattern. This work focuses on the online adaptive monitoring of high-dimensional data in resource-constrained environments with multiple potential failure modes. To achieve this, we propose to apply the Shiryaev-Roberts procedure on the failure mode level and utilize the multi-arm bandit to balance the exploration and exploitation. We further discuss the theoretical property of the proposed algorithm to show that the proposed method can correctly isolate the failure mode. Finally, extensive simulations and two case studies demonstrate that the change point detection performance and the failure mode isolation accuracy can be greatly improved.

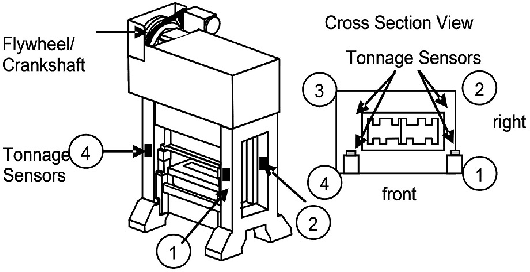
Adaptive Resources Allocation CUSUM for Binomial Count Data Monitoring with Application to COVID-19 Hotspot Detection

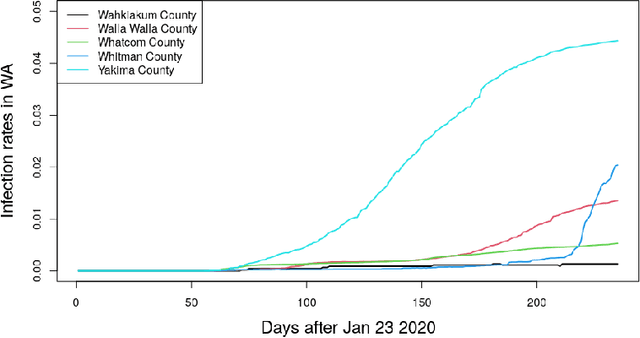
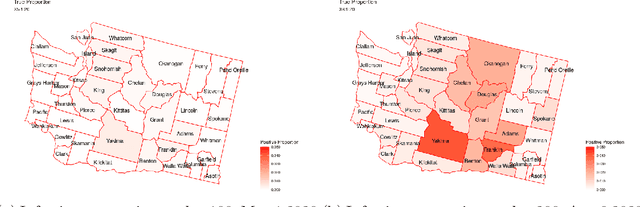
In this paper, we present an efficient statistical method (denoted as "Adaptive Resources Allocation CUSUM") to robustly and efficiently detect the hotspot with limited sampling resources. Our main idea is to combine the multi-arm bandit (MAB) and change-point detection methods to balance the exploration and exploitation of resource allocation for hotspot detection. Further, a Bayesian weighted update is used to update the posterior distribution of the infection rate. Then, the upper confidence bound (UCB) is used for resource allocation and planning. Finally, CUSUM monitoring statistics to detect the change point as well as the change location. For performance evaluation, we compare the performance of the proposed method with several benchmark methods in the literature and showed the proposed algorithm is able to achieve a lower detection delay and higher detection precision. Finally, this method is applied to hotspot detection in a real case study of county-level daily positive COVID-19 cases in Washington State WA) and demonstrates the effectiveness with very limited distributed samples.

The Directional Bias Helps Stochastic Gradient Descent to Generalize in Kernel Regression Models

We study the Stochastic Gradient Descent (SGD) algorithm in nonparametric statistics: kernel regression in particular. The directional bias property of SGD, which is known in the linear regression setting, is generalized to the kernel regression. More specifically, we prove that SGD with moderate and annealing step-size converges along the direction of the eigenvector that corresponds to the largest eigenvalue of the Gram matrix. In addition, the Gradient Descent (GD) with a moderate or small step-size converges along the direction that corresponds to the smallest eigenvalue. These facts are referred to as the directional bias properties; they may interpret how an SGD-computed estimator has a potentially smaller generalization error than a GD-computed estimator. The application of our theory is demonstrated by simulation studies and a case study that is based on the FashionMNIST dataset.

Implicit Regularization Properties of Variance Reduced Stochastic Mirror Descent

In machine learning and statistical data analysis, we often run into objective function that is a summation: the number of terms in the summation possibly is equal to the sample size, which can be enormous. In such a setting, the stochastic mirror descent (SMD) algorithm is a numerically efficient method -- each iteration involving a very small subset of the data. The variance reduction version of SMD (VRSMD) can further improve SMD by inducing faster convergence. On the other hand, algorithms such as gradient descent and stochastic gradient descent have the implicit regularization property that leads to better performance in terms of the generalization errors. Little is known on whether such a property holds for VRSMD. We prove here that the discrete VRSMD estimator sequence converges to the minimum mirror interpolant in the linear regression. This establishes the implicit regularization property for VRSMD. As an application of the above result, we derive a model estimation accuracy result in the setting when the true model is sparse. We use numerical examples to illustrate the empirical power of VRSMD.

Private Sequential Hypothesis Testing for Statisticians: Privacy, Error Rates, and Sample Size

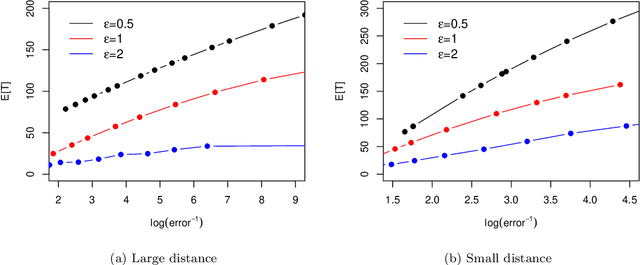
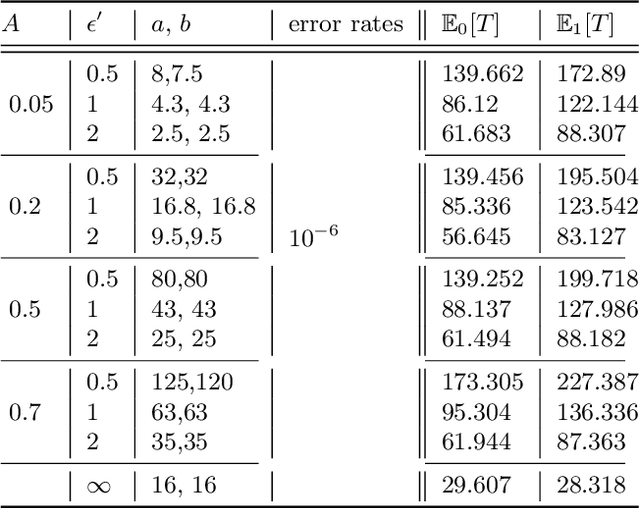
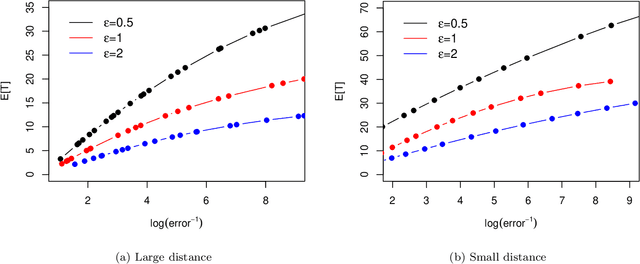
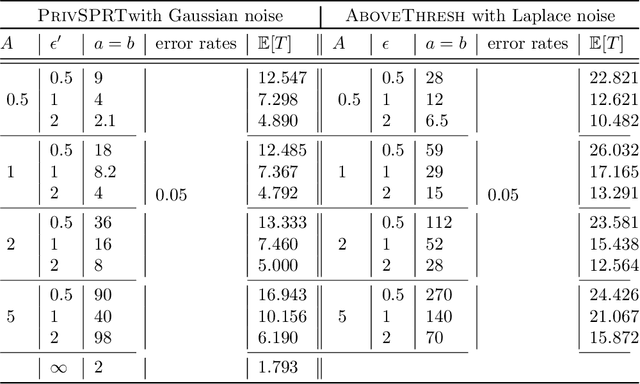
The sequential hypothesis testing problem is a class of statistical analyses where the sample size is not fixed in advance. Instead, the decision-process takes in new observations sequentially to make real-time decisions for testing an alternative hypothesis against a null hypothesis until some stopping criterion is satisfied. In many common applications of sequential hypothesis testing, the data can be highly sensitive and may require privacy protection; for example, sequential hypothesis testing is used in clinical trials, where doctors sequentially collect data from patients and must determine when to stop recruiting patients and whether the treatment is effective. The field of differential privacy has been developed to offer data analysis tools with strong privacy guarantees, and has been commonly applied to machine learning and statistical tasks. In this work, we study the sequential hypothesis testing problem under a slight variant of differential privacy, known as Renyi differential privacy. We present a new private algorithm based on Wald's Sequential Probability Ratio Test (SPRT) that also gives strong theoretical privacy guarantees. We provide theoretical analysis on statistical performance measured by Type I and Type II error as well as the expected sample size. We also empirically validate our theoretical results on several synthetic databases, showing that our algorithms also perform well in practice. Unlike previous work in private hypothesis testing that focused only on the classical fixed sample setting, our results in the sequential setting allow a conclusion to be reached much earlier, and thus saving the cost of collecting additional samples.

Active Learning-Based Multistage Sequential Decision-Making Model with Application on Common Bile Duct Stone Evaluation

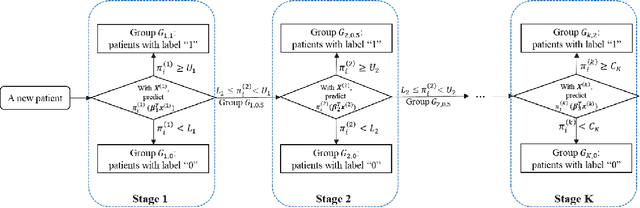
Multistage sequential decision-making scenarios are commonly seen in the healthcare diagnosis process. In this paper, an active learning-based method is developed to actively collect only the necessary patient data in a sequential manner. There are two novelties in the proposed method. First, unlike the existing ordinal logistic regression model which only models a single stage, we estimate the parameters for all stages together. Second, it is assumed that the coefficients for common features in different stages are kept consistent. The effectiveness of the proposed method is validated in both a simulation study and a real case study. Compared with the baseline method where the data is modeled individually and independently, the proposed method improves the estimation efficiency by 62\%-1838\%. For both simulation and testing cohorts, the proposed method is more effective, stable, interpretable, and computationally efficient on parameter estimation. The proposed method can be easily extended to a variety of scenarios where decision-making can be done sequentially with only necessary information.

Asymptotic Theory of $\ell_1$-Regularized PDE Identification from a Single Noisy Trajectory

We prove the support recovery for a general class of linear and nonlinear evolutionary partial differential equation (PDE) identification from a single noisy trajectory using $\ell_1$ regularized Pseudo-Least Squares model~($\ell_1$-PsLS). In any associative $\mathbb{R}$-algebra generated by finitely many differentiation operators that contain the unknown PDE operator, applying $\ell_1$-PsLS to a given data set yields a family of candidate models with coefficients $\mathbf{c}(\lambda)$ parameterized by the regularization weight $\lambda\geq 0$. The trace of $\{\mathbf{c}(\lambda)\}_{\lambda\geq 0}$ suffers from high variance due to data noises and finite difference approximation errors. We provide a set of sufficient conditions which guarantee that, from a single trajectory data denoised by a Local-Polynomial filter, the support of $\mathbf{c}(\lambda)$ asymptotically converges to the true signed-support associated with the underlying PDE for sufficiently many data and a certain range of $\lambda$. We also show various numerical experiments to validate our theory.