Active Learning-Based Multistage Sequential Decision-Making Model with Application on Common Bile Duct Stone Evaluation

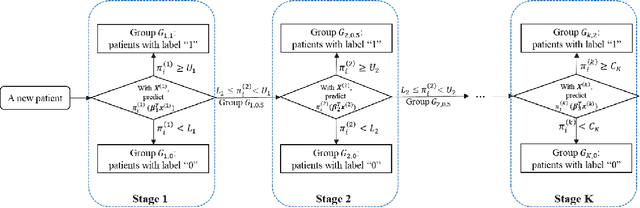
Multistage sequential decision-making scenarios are commonly seen in the healthcare diagnosis process. In this paper, an active learning-based method is developed to actively collect only the necessary patient data in a sequential manner. There are two novelties in the proposed method. First, unlike the existing ordinal logistic regression model which only models a single stage, we estimate the parameters for all stages together. Second, it is assumed that the coefficients for common features in different stages are kept consistent. The effectiveness of the proposed method is validated in both a simulation study and a real case study. Compared with the baseline method where the data is modeled individually and independently, the proposed method improves the estimation efficiency by 62\%-1838\%. For both simulation and testing cohorts, the proposed method is more effective, stable, interpretable, and computationally efficient on parameter estimation. The proposed method can be easily extended to a variety of scenarios where decision-making can be done sequentially with only necessary information.

APIK: Active Physics-Informed Kriging Model with Partial Differential Equations

Kriging (or Gaussian process regression) is a popular machine learning method for its flexibility and closed-form prediction expressions. However, one of the key challenges in applying kriging to engineering systems is that the available measurement data is scarce due to the measurement limitations and high sensing costs. On the other hand, physical knowledge of the engineering system is often available and represented in the form of partial differential equations (PDEs). We present in this work a PDE Informed Kriging model (PIK), which introduces PDE information via a set of PDE points and conducts posterior prediction similar to the standard kriging method. The proposed PIK model can incorporate physical knowledge from both linear and nonlinear PDEs. To further improve learning performance, we propose an Active PIK framework (APIK) that designs PDE points to leverage the PDE information based on the PIK model and measurement data. The selected PDE points not only explore the whole input space but also exploit the locations where the PDE information is critical in reducing predictive uncertainty. Finally, an expectation-maximization algorithm is developed for parameter estimation. We demonstrate the effectiveness of APIK in two synthetic examples, a shock wave case study, and a laser heating case study.

Additive Tensor Decomposition Considering Structural Data Information

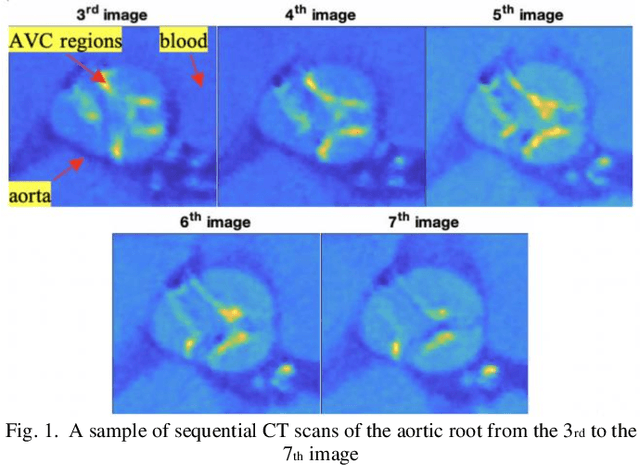
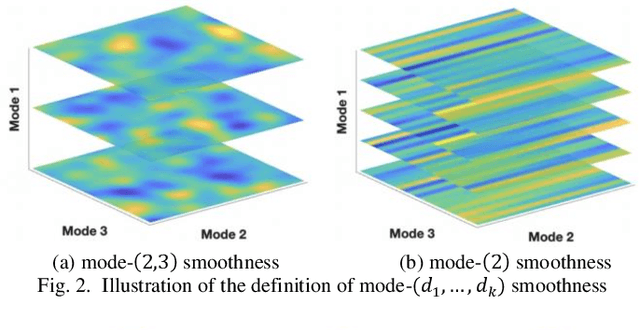
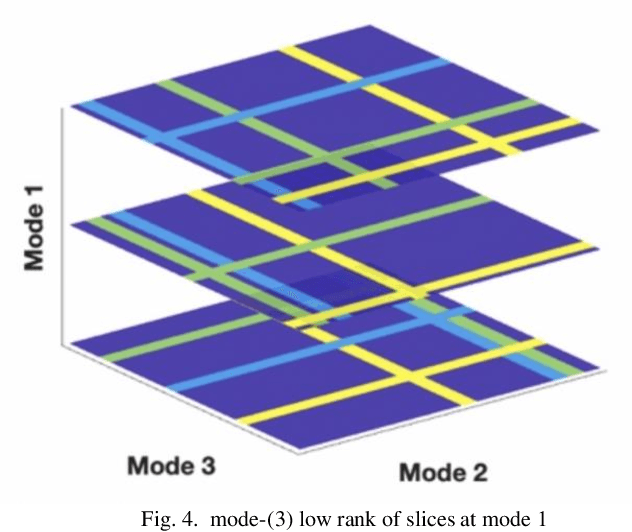
Tensor data with rich structural information becomes increasingly important in process modeling, monitoring, and diagnosis. Here structural information is referred to structural properties such as sparsity, smoothness, low-rank, and piecewise constancy. To reveal useful information from tensor data, we propose to decompose the tensor into the summation of multiple components based on different structural information of them. In this paper, we provide a new definition of structural information in tensor data. Based on it, we propose an additive tensor decomposition (ATD) framework to extract useful information from tensor data. This framework specifies a high dimensional optimization problem to obtain the components with distinct structural information. An alternating direction method of multipliers (ADMM) algorithm is proposed to solve it, which is highly parallelable and thus suitable for the proposed optimization problem. Two simulation examples and a real case study in medical image analysis illustrate the versatility and effectiveness of the ATD framework.

AVP: Physics-informed Data Generation for Small-data Learning

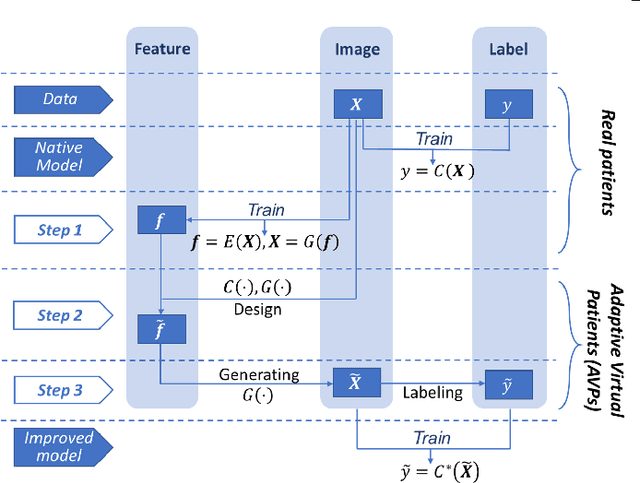
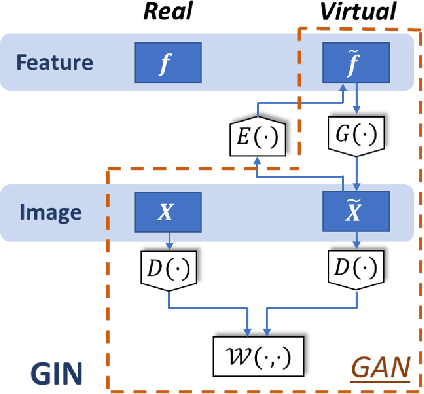
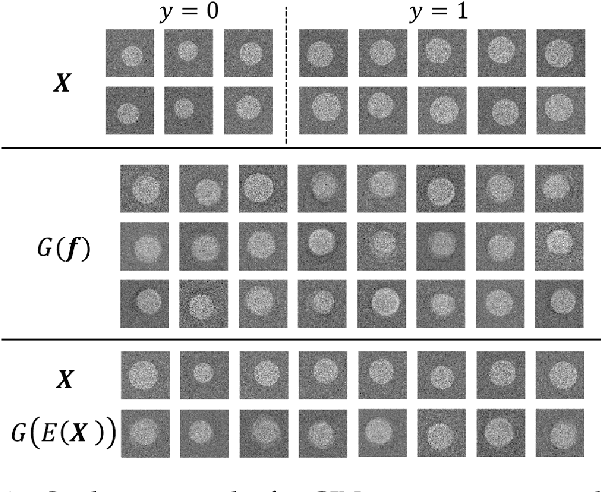
Deep neural networks have achieved great success in multiple learning problems, and attracted increasing attention from the medicine community. In reality, however, the limited availability and high costs of medical data is a major challenge of applying deep neural networks to computer-aided diagnosis and treatment planning. We address this challenge with adaptive virtual patients (AVPs) and the associated physics-informed learning framework. Specifically, the original training dataset is fused with an additional dataset of AVPs, which are generated by a data-driven model and the associated supervision (e.g., labels) is obtained by a physics-based approach. A key novelty in the proposed framework is the bidirectional and uncoupled generative invertible networks (GIN), which can extract pathophysiological features from the training medical image and generate pathophysiologically meaningful virtual patients. In order to mitigate the possibly high labeling cost of physical experiments, a $\mu$-measure design is conducted: this allows the AVPs to not only further explore the uncertain regions, but also balance the label distribution. We then discuss the pathophysiological interpretability of GIN both theoretically and experimentally, and demonstrate the effectiveness of AVPs using a real medical image dataset, in which the proposed AVPs lower the labeling cost by 90% while achieving a 15% improvement in prediction accuracy.

Generative Invertible Networks (GIN): Pathophysiology-Interpretable Feature Mapping and Virtual Patient Generation

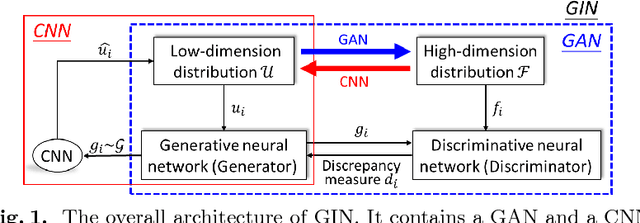
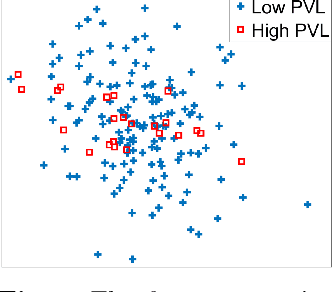
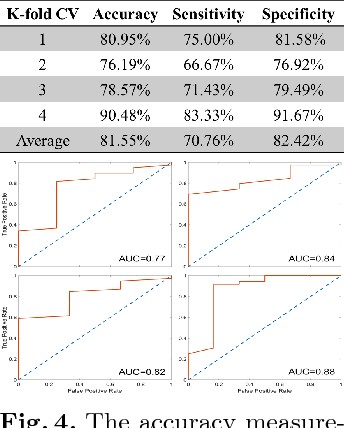
Machine learning methods play increasingly important roles in pre-procedural planning for complex surgeries and interventions. Very often, however, researchers find the historical records of emerging surgical techniques, such as the transcatheter aortic valve replacement (TAVR), are highly scarce in quantity. In this paper, we address this challenge by proposing novel generative invertible networks (GIN) to select features and generate high-quality virtual patients that may potentially serve as an additional data source for machine learning. Combining a convolutional neural network (CNN) and generative adversarial networks (GAN), GIN discovers the pathophysiologic meaning of the feature space. Moreover, a test of predicting the surgical outcome directly using the selected features results in a high accuracy of 81.55%, which suggests little pathophysiologic information has been lost while conducting the feature selection. This demonstrates GIN can generate virtual patients not only visually authentic but also pathophysiologically interpretable.