Solving Sparse \& High-Dimensional-Output Regression via Compression

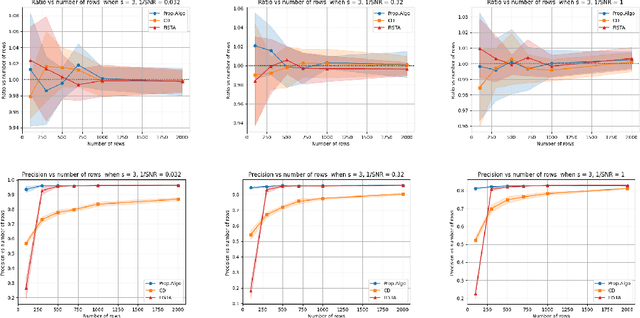
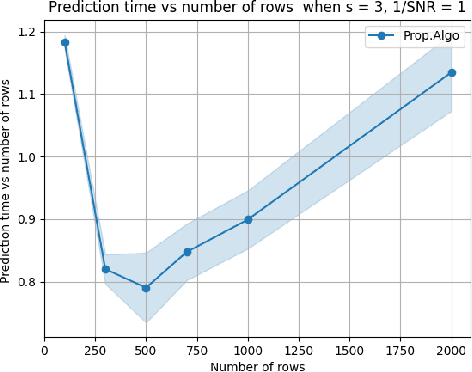
Multi-Output Regression (MOR) has been widely used in scientific data analysis for decision-making. Unlike traditional regression models, MOR aims to simultaneously predict multiple real-valued outputs given an input. However, the increasing dimensionality of the outputs poses significant challenges regarding interpretability and computational scalability for modern MOR applications. As a first step to address these challenges, this paper proposes a Sparse \& High-dimensional-Output REgression (SHORE) model by incorporating additional sparsity requirements to resolve the output interpretability, and then designs a computationally efficient two-stage optimization framework capable of solving SHORE with provable accuracy via compression on outputs. Theoretically, we show that the proposed framework is computationally scalable while maintaining the same order of training loss and prediction loss before-and-after compression under arbitrary or relatively weak sample set conditions. Empirically, numerical results further validate the theoretical findings, showcasing the efficiency and accuracy of the proposed framework.

Boosting Imperceptibility of Stable Diffusion-based Adversarial Examples Generation with Momentum

We propose a novel framework, Stable Diffusion-based Momentum Integrated Adversarial Examples (SD-MIAE), for generating adversarial examples that can effectively mislead neural network classifiers while maintaining visual imperceptibility and preserving the semantic similarity to the original class label. Our method leverages the text-to-image generation capabilities of the Stable Diffusion model by manipulating token embeddings corresponding to the specified class in its latent space. These token embeddings guide the generation of adversarial images that maintain high visual fidelity. The SD-MIAE framework consists of two phases: (1) an initial adversarial optimization phase that modifies token embeddings to produce misclassified yet natural-looking images and (2) a momentum-based optimization phase that refines the adversarial perturbations. By introducing momentum, our approach stabilizes the optimization of perturbations across iterations, enhancing both the misclassification rate and visual fidelity of the generated adversarial examples. Experimental results demonstrate that SD-MIAE achieves a high misclassification rate of 79%, improving by 35% over the state-of-the-art method while preserving the imperceptibility of adversarial perturbations and the semantic similarity to the original class label, making it a practical method for robust adversarial evaluation.

Robust Multi-Agent Reinforcement Learning via Adversarial Regularization: Theoretical Foundation and Stable Algorithms

Multi-Agent Reinforcement Learning (MARL) has shown promising results across several domains. Despite this promise, MARL policies often lack robustness and are therefore sensitive to small changes in their environment. This presents a serious concern for the real world deployment of MARL algorithms, where the testing environment may slightly differ from the training environment. In this work we show that we can gain robustness by controlling a policy's Lipschitz constant, and under mild conditions, establish the existence of a Lipschitz and close-to-optimal policy. Based on these insights, we propose a new robust MARL framework, ERNIE, that promotes the Lipschitz continuity of the policies with respect to the state observations and actions by adversarial regularization. The ERNIE framework provides robustness against noisy observations, changing transition dynamics, and malicious actions of agents. However, ERNIE's adversarial regularization may introduce some training instability. To reduce this instability, we reformulate adversarial regularization as a Stackelberg game. We demonstrate the effectiveness of the proposed framework with extensive experiments in traffic light control and particle environments. In addition, we extend ERNIE to mean-field MARL with a formulation based on distributionally robust optimization that outperforms its non-robust counterpart and is of independent interest. Our code is available at https://github.com/abukharin3/ERNIE.

Invisible Watermarking for Audio Generation Diffusion Models

Diffusion models have gained prominence in the image domain for their capabilities in data generation and transformation, achieving state-of-the-art performance in various tasks in both image and audio domains. In the rapidly evolving field of audio-based machine learning, safeguarding model integrity and establishing data copyright are of paramount importance. This paper presents the first watermarking technique applied to audio diffusion models trained on mel-spectrograms. This offers a novel approach to the aforementioned challenges. Our model excels not only in benign audio generation, but also incorporates an invisible watermarking trigger mechanism for model verification. This watermark trigger serves as a protective layer, enabling the identification of model ownership and ensuring its integrity. Through extensive experiments, we demonstrate that invisible watermark triggers can effectively protect against unauthorized modifications while maintaining high utility in benign audio generation tasks.

APIK: Active Physics-Informed Kriging Model with Partial Differential Equations

Kriging (or Gaussian process regression) is a popular machine learning method for its flexibility and closed-form prediction expressions. However, one of the key challenges in applying kriging to engineering systems is that the available measurement data is scarce due to the measurement limitations and high sensing costs. On the other hand, physical knowledge of the engineering system is often available and represented in the form of partial differential equations (PDEs). We present in this work a PDE Informed Kriging model (PIK), which introduces PDE information via a set of PDE points and conducts posterior prediction similar to the standard kriging method. The proposed PIK model can incorporate physical knowledge from both linear and nonlinear PDEs. To further improve learning performance, we propose an Active PIK framework (APIK) that designs PDE points to leverage the PDE information based on the PIK model and measurement data. The selected PDE points not only explore the whole input space but also exploit the locations where the PDE information is critical in reducing predictive uncertainty. Finally, an expectation-maximization algorithm is developed for parameter estimation. We demonstrate the effectiveness of APIK in two synthetic examples, a shock wave case study, and a laser heating case study.

On Computation and Generalization of GANs with Spectrum Control

Generative Adversarial Networks (GANs), though powerful, is hard to train. Several recent works (brock2016neural,miyato2018spectral) suggest that controlling the spectra of weight matrices in the discriminator can significantly improve the training of GANs. Motivated by their discovery, we propose a new framework for training GANs, which allows more flexible spectrum control (e.g., making the weight matrices of the discriminator have slow singular value decays). Specifically, we propose a new reparameterization approach for the weight matrices of the discriminator in GANs, which allows us to directly manipulate the spectra of the weight matrices through various regularizers and constraints, without intensively computing singular value decompositions. Theoretically, we further show that the spectrum control improves the generalization ability of GANs. Our experiments on CIFAR-10, STL-10, and ImageNet datasets confirm that compared to other methods, our proposed method is capable of generating images with competitive quality by utilizing spectral normalization and encouraging the slow singular value decay.

Learning to Defense by Learning to Attack

Adversarial training provides a principled approach for training robust neural networks. From an optimization perspective, the adversarial training is essentially solving a minmax robust optimization problem. The outer minimization is trying to learn a robust classifier, while the inner maximization is trying to generate adversarial samples. Unfortunately, such a minmax problem is very difficult to solve due to the lack of convex-concave structure. This work proposes a new adversarial training method based on a general learning-to-learn framework. Specifically, instead of applying the existing hand-design algorithms for the inner problem, we learn an optimizer, which is parametrized as a convolutional neural network. At the same time, a robust classifier is learned to defense the adversarial attack generated by the learned optimizer. Our experiments demonstrate that our proposed method significantly outperforms existing adversarial training methods on CIFAR-10 and CIFAR-100 datasets.

On Landscape of Lagrangian Functions and Stochastic Search for Constrained Nonconvex Optimization

We study constrained nonconvex optimization problems in machine learning, signal processing, and stochastic control. It is well-known that these problems can be rewritten to a minimax problem in a Lagrangian form. However, due to the lack of convexity, their landscape is not well understood and how to find the stable equilibria of the Lagrangian function is still unknown. To bridge the gap, we study the landscape of the Lagrangian function. Further, we define a special class of Lagrangian functions. They enjoy two properties: 1.Equilibria are either stable or unstable (Formal definition in Section 2); 2.Stable equilibria correspond to the global optima of the original problem. We show that a generalized eigenvalue (GEV) problem, including canonical correlation analysis and other problems, belongs to the class. Specifically, we characterize its stable and unstable equilibria by leveraging an invariant group and symmetric property (more details in Section 3). Motivated by these neat geometric structures, we propose a simple, efficient, and stochastic primal-dual algorithm solving the online GEV problem. Theoretically, we provide sufficient conditions, based on which we establish an asymptotic convergence rate and obtain the first sample complexity result for the online GEV problem by diffusion approximations, which are widely used in applied probability and stochastic control. Numerical results are provided to support our theory.

Toward Deeper Understanding of Nonconvex Stochastic Optimization with Momentum using Diffusion Approximations

Momentum Stochastic Gradient Descent (MSGD) algorithm has been widely applied to many nonconvex optimization problems in machine learning. Popular examples include training deep neural networks, dimensionality reduction, and etc. Due to the lack of convexity and the extra momentum term, the optimization theory of MSGD is still largely unknown. In this paper, we study this fundamental optimization algorithm based on the so-called "strict saddle problem." By diffusion approximation type analysis, our study shows that the momentum helps escape from saddle points, but hurts the convergence within the neighborhood of optima (if without the step size annealing). Our theoretical discovery partially corroborates the empirical success of MSGD in training deep neural networks. Moreover, our analysis applies the martingale method and "Fixed-State-Chain" method from the stochastic approximation literature, which are of independent interest.

Dropping Convexity for More Efficient and Scalable Online Multiview Learning

Multiview representation learning is very popular for latent factor analysis. It naturally arises in many data analysis, machine learning, and information retrieval applications to model dependent structures among multiple data sources. For computational convenience, existing approaches usually formulate the multiview representation learning as convex optimization problems, where global optima can be obtained by certain algorithms in polynomial time. However, many pieces of evidence have corroborated that heuristic nonconvex approaches also have good empirical computational performance and convergence to the global optima, although there is a lack of theoretical justification. Such a gap between theory and practice motivates us to study a nonconvex formulation for multiview representation learning, which can be efficiently solved by a simple stochastic gradient descent (SGD) algorithm. We first illustrate the geometry of the nonconvex formulation; Then, we establish asymptotic global rates of convergence to the global optima by diffusion approximations. Numerical experiments are provided to support our theory.