Additive Tensor Decomposition Considering Structural Data Information
Paper and Code
Jul 27, 2020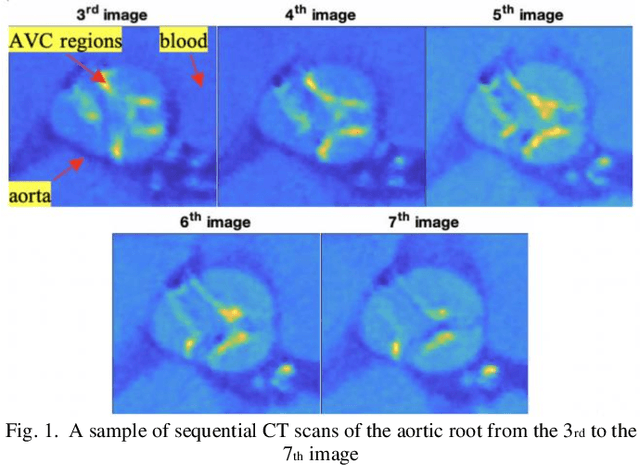
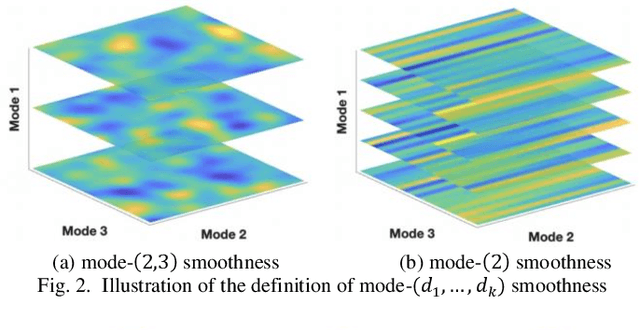

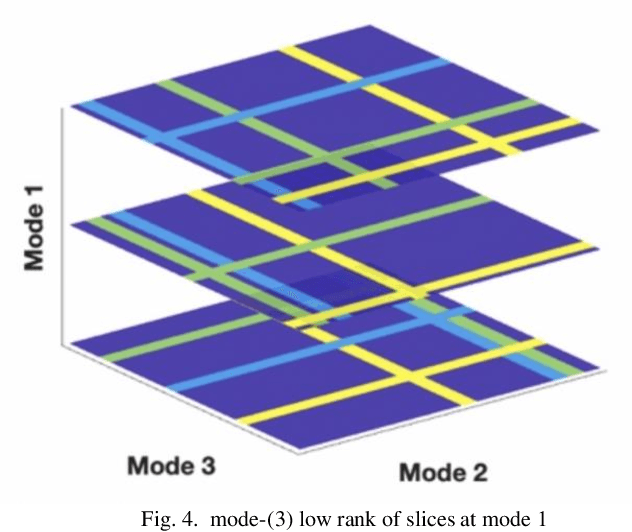
Tensor data with rich structural information becomes increasingly important in process modeling, monitoring, and diagnosis. Here structural information is referred to structural properties such as sparsity, smoothness, low-rank, and piecewise constancy. To reveal useful information from tensor data, we propose to decompose the tensor into the summation of multiple components based on different structural information of them. In this paper, we provide a new definition of structural information in tensor data. Based on it, we propose an additive tensor decomposition (ATD) framework to extract useful information from tensor data. This framework specifies a high dimensional optimization problem to obtain the components with distinct structural information. An alternating direction method of multipliers (ADMM) algorithm is proposed to solve it, which is highly parallelable and thus suitable for the proposed optimization problem. Two simulation examples and a real case study in medical image analysis illustrate the versatility and effectiveness of the ATD framework.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge