Differential Privacy Under Class Imbalance: Methods and Empirical Insights

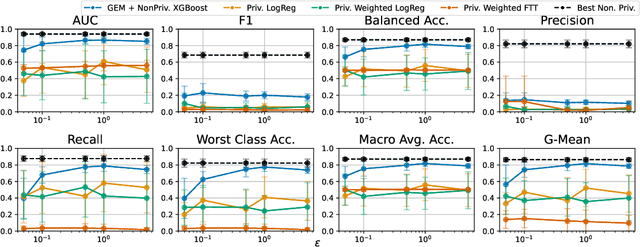
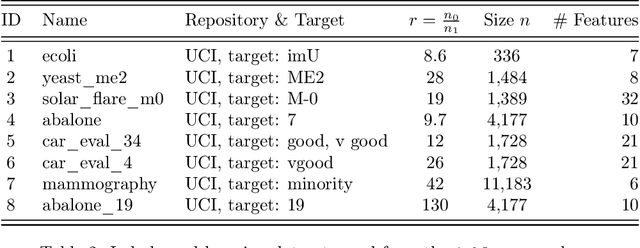
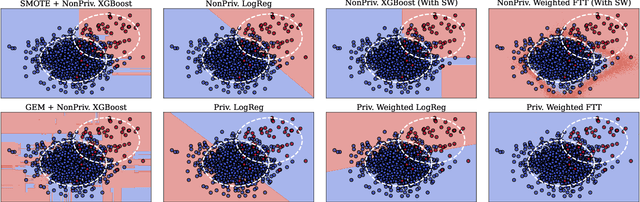
Imbalanced learning occurs in classification settings where the distribution of class-labels is highly skewed in the training data, such as when predicting rare diseases or in fraud detection. This class imbalance presents a significant algorithmic challenge, which can be further exacerbated when privacy-preserving techniques such as differential privacy are applied to protect sensitive training data. Our work formalizes these challenges and provides a number of algorithmic solutions. We consider DP variants of pre-processing methods that privately augment the original dataset to reduce the class imbalance; these include oversampling, SMOTE, and private synthetic data generation. We also consider DP variants of in-processing techniques, which adjust the learning algorithm to account for the imbalance; these include model bagging, class-weighted empirical risk minimization and class-weighted deep learning. For each method, we either adapt an existing imbalanced learning technique to the private setting or demonstrate its incompatibility with differential privacy. Finally, we empirically evaluate these privacy-preserving imbalanced learning methods under various data and distributional settings. We find that private synthetic data methods perform well as a data pre-processing step, while class-weighted ERMs are an alternative in higher-dimensional settings where private synthetic data suffers from the curse of dimensionality.

Thompson Sampling Itself is Differentially Private

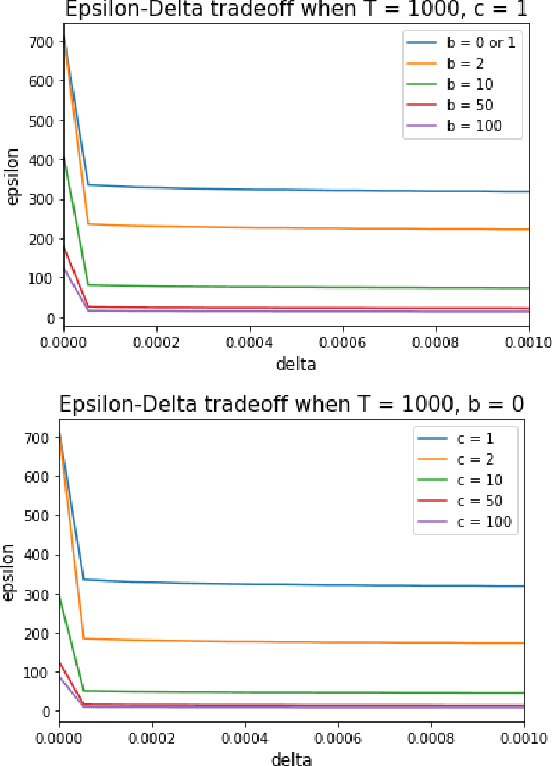
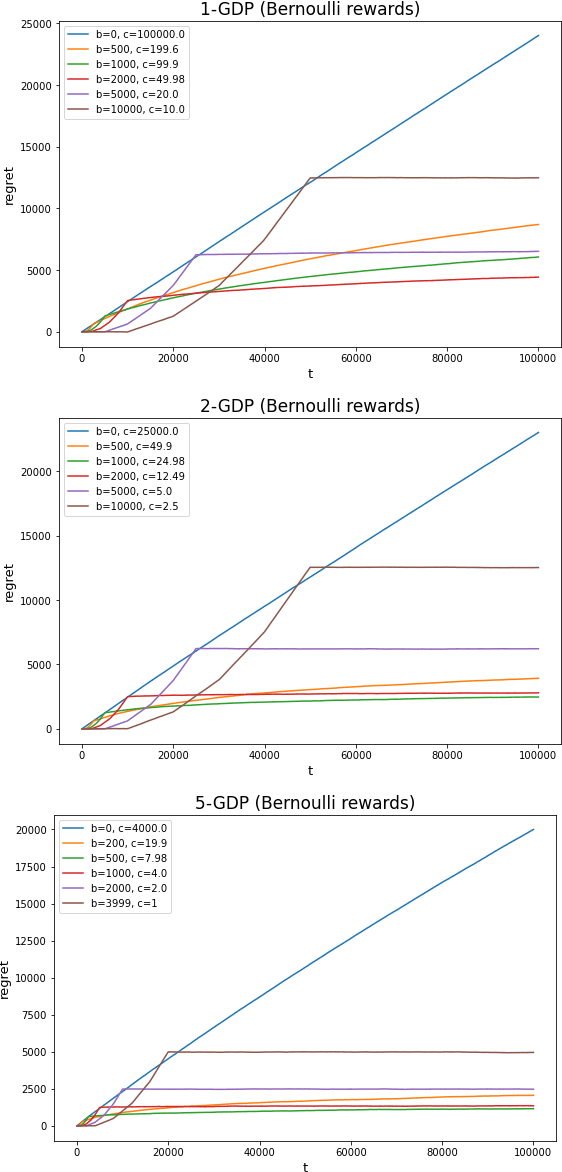
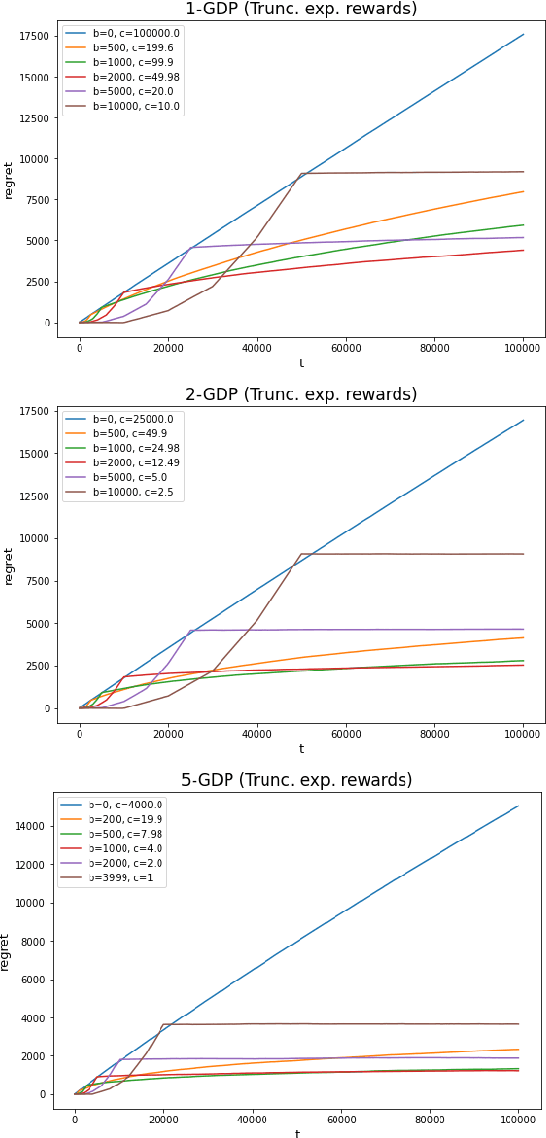
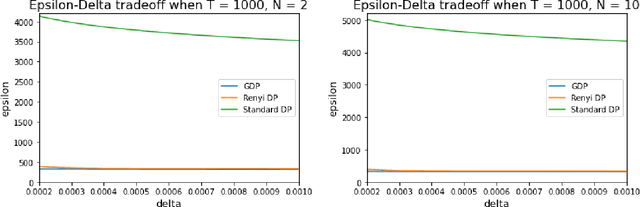
In this work we first show that the classical Thompson sampling algorithm for multi-arm bandits is differentially private as-is, without any modification. We provide per-round privacy guarantees as a function of problem parameters and show composition over $T$ rounds; since the algorithm is unchanged, existing $O(\sqrt{NT\log N})$ regret bounds still hold and there is no loss in performance due to privacy. We then show that simple modifications -- such as pre-pulling all arms a fixed number of times, increasing the sampling variance -- can provide tighter privacy guarantees. We again provide privacy guarantees that now depend on the new parameters introduced in the modification, which allows the analyst to tune the privacy guarantee as desired. We also provide a novel regret analysis for this new algorithm, and show how the new parameters also impact expected regret. Finally, we empirically validate and illustrate our theoretical findings in two parameter regimes and demonstrate that tuning the new parameters substantially improve the privacy-regret tradeoff.

Mean Estimation with User-level Privacy under Data Heterogeneity

A key challenge in many modern data analysis tasks is that user data are heterogeneous. Different users may possess vastly different numbers of data points. More importantly, it cannot be assumed that all users sample from the same underlying distribution. This is true, for example in language data, where different speech styles result in data heterogeneity. In this work we propose a simple model of heterogeneous user data that allows user data to differ in both distribution and quantity of data, and provide a method for estimating the population-level mean while preserving user-level differential privacy. We demonstrate asymptotic optimality of our estimator and also prove general lower bounds on the error achievable in the setting we introduce.

Differentially Private Synthetic Control

Synthetic control is a causal inference tool used to estimate the treatment effects of an intervention by creating synthetic counterfactual data. This approach combines measurements from other similar observations (i.e., donor pool ) to predict a counterfactual time series of interest (i.e., target unit) by analyzing the relationship between the target and the donor pool before the intervention. As synthetic control tools are increasingly applied to sensitive or proprietary data, formal privacy protections are often required. In this work, we provide the first algorithms for differentially private synthetic control with explicit error bounds. Our approach builds upon tools from non-private synthetic control and differentially private empirical risk minimization. We provide upper and lower bounds on the sensitivity of the synthetic control query and provide explicit error bounds on the accuracy of our private synthetic control algorithms. We show that our algorithms produce accurate predictions for the target unit, and that the cost of privacy is small. Finally, we empirically evaluate the performance of our algorithm, and show favorable performance in a variety of parameter regimes, as well as providing guidance to practitioners for hyperparameter tuning.

Robust Estimation under the Wasserstein Distance

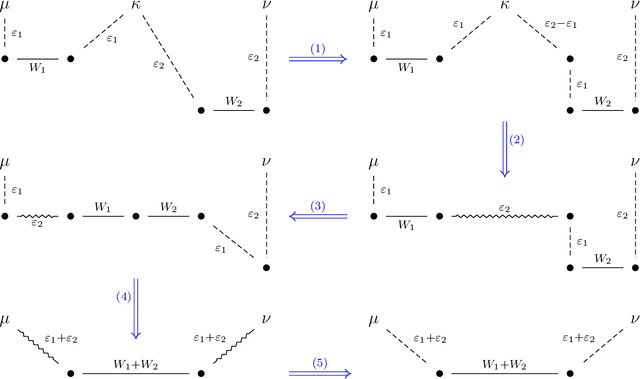
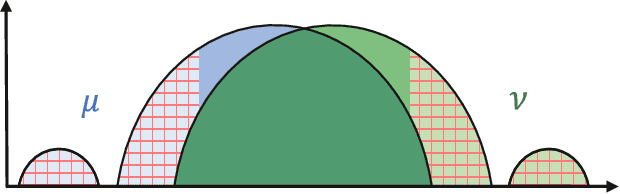
We study the problem of robust distribution estimation under the Wasserstein metric, a popular discrepancy measure between probability distributions rooted in optimal transport (OT) theory. We introduce a new outlier-robust Wasserstein distance $\mathsf{W}_p^\varepsilon$ which allows for $\varepsilon$ outlier mass to be removed from its input distributions, and show that minimum distance estimation under $\mathsf{W}_p^\varepsilon$ achieves minimax optimal robust estimation risk. Our analysis is rooted in several new results for partial OT, including an approximate triangle inequality, which may be of independent interest. To address computational tractability, we derive a dual formulation for $\mathsf{W}_p^\varepsilon$ that adds a simple penalty term to the classic Kantorovich dual objective. As such, $\mathsf{W}_p^\varepsilon$ can be implemented via an elementary modification to standard, duality-based OT solvers. Our results are extended to sliced OT, where distributions are projected onto low-dimensional subspaces, and applications to homogeneity and independence testing are explored. We illustrate the virtues of our framework via applications to generative modeling with contaminated datasets.

Private Sequential Hypothesis Testing for Statisticians: Privacy, Error Rates, and Sample Size

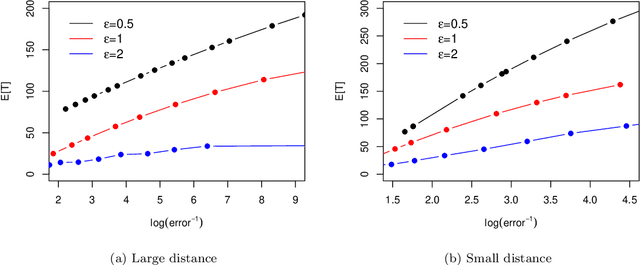
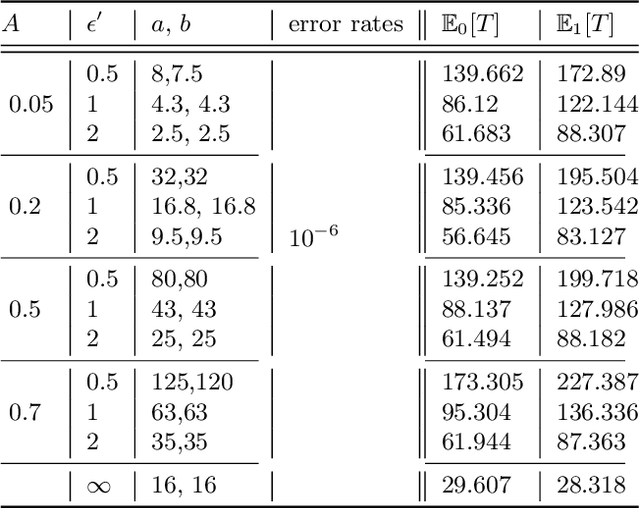
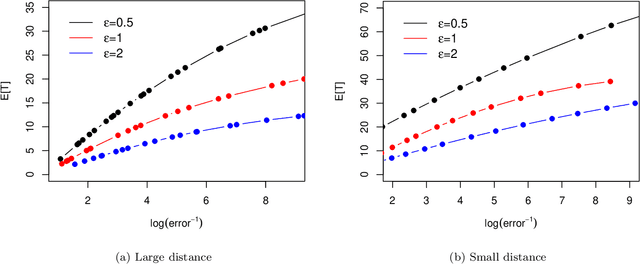
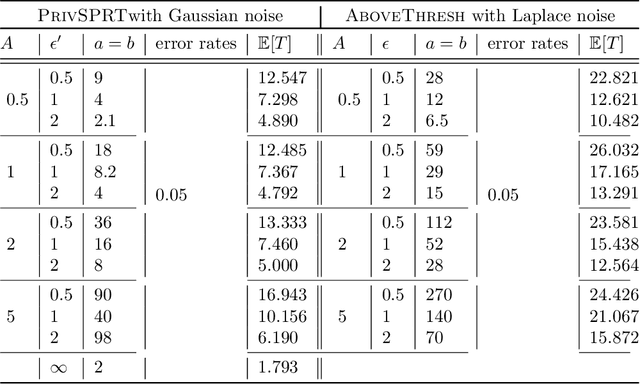
The sequential hypothesis testing problem is a class of statistical analyses where the sample size is not fixed in advance. Instead, the decision-process takes in new observations sequentially to make real-time decisions for testing an alternative hypothesis against a null hypothesis until some stopping criterion is satisfied. In many common applications of sequential hypothesis testing, the data can be highly sensitive and may require privacy protection; for example, sequential hypothesis testing is used in clinical trials, where doctors sequentially collect data from patients and must determine when to stop recruiting patients and whether the treatment is effective. The field of differential privacy has been developed to offer data analysis tools with strong privacy guarantees, and has been commonly applied to machine learning and statistical tasks. In this work, we study the sequential hypothesis testing problem under a slight variant of differential privacy, known as Renyi differential privacy. We present a new private algorithm based on Wald's Sequential Probability Ratio Test (SPRT) that also gives strong theoretical privacy guarantees. We provide theoretical analysis on statistical performance measured by Type I and Type II error as well as the expected sample size. We also empirically validate our theoretical results on several synthetic databases, showing that our algorithms also perform well in practice. Unlike previous work in private hypothesis testing that focused only on the classical fixed sample setting, our results in the sequential setting allow a conclusion to be reached much earlier, and thus saving the cost of collecting additional samples.

Outlier-Robust Optimal Transport: Duality, Structure, and Statistical Analysis

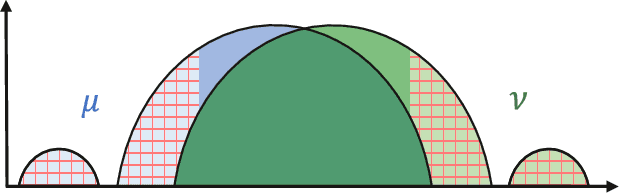
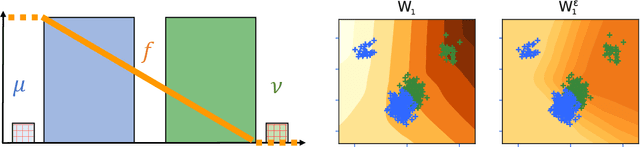
The Wasserstein distance, rooted in optimal transport (OT) theory, is a popular discrepancy measure between probability distributions with various applications to statistics and machine learning. Despite their rich structure and demonstrated utility, Wasserstein distances are sensitive to outliers in the considered distributions, which hinders applicability in practice. Inspired by the Huber contamination model, we propose a new outlier-robust Wasserstein distance $\mathsf{W}_p^\varepsilon$ which allows for $\varepsilon$ outlier mass to be removed from each contaminated distribution. Our formulation amounts to a highly regular optimization problem that lends itself better for analysis compared to previously considered frameworks. Leveraging this, we conduct a thorough theoretical study of $\mathsf{W}_p^\varepsilon$, encompassing characterization of optimal perturbations, regularity, duality, and statistical estimation and robustness results. In particular, by decoupling the optimization variables, we arrive at a simple dual form for $\mathsf{W}_p^\varepsilon$ that can be implemented via an elementary modification to standard, duality-based OT solvers. We illustrate the benefits of our framework via applications to generative modeling with contaminated datasets.

Differentially Private Normalizing Flows for Privacy-Preserving Density Estimation

Normalizing flow models have risen as a popular solution to the problem of density estimation, enabling high-quality synthetic data generation as well as exact probability density evaluation. However, in contexts where individuals are directly associated with the training data, releasing such a model raises privacy concerns. In this work, we propose the use of normalizing flow models that provide explicit differential privacy guarantees as a novel approach to the problem of privacy-preserving density estimation. We evaluate the efficacy of our approach empirically using benchmark datasets, and we demonstrate that our method substantially outperforms previous state-of-the-art approaches. We additionally show how our algorithm can be applied to the task of differentially private anomaly detection.

Differentially Private Online Submodular Maximization

In this work we consider the problem of online submodular maximization under a cardinality constraint with differential privacy (DP). A stream of $T$ submodular functions over a common finite ground set $U$ arrives online, and at each time-step the decision maker must choose at most $k$ elements of $U$ before observing the function. The decision maker obtains a payoff equal to the function evaluated on the chosen set, and aims to learn a sequence of sets that achieves low expected regret. In the full-information setting, we develop an $(\varepsilon,\delta)$-DP algorithm with expected $(1-1/e)$-regret bound of $\mathcal{O}\left( \frac{k^2\log |U|\sqrt{T \log k/\delta}}{\varepsilon} \right)$. This algorithm contains $k$ ordered experts that learn the best marginal increments for each item over the whole time horizon while maintaining privacy of the functions. In the bandit setting, we provide an $(\varepsilon,\delta+ O(e^{-T^{1/3}}))$-DP algorithm with expected $(1-1/e)$-regret bound of $\mathcal{O}\left( \frac{\sqrt{\log k/\delta}}{\varepsilon} (k (|U| \log |U|)^{1/3})^2 T^{2/3} \right)$. Our algorithms contains $k$ ordered experts that learn the best marginal item to select given the items chosen her predecessors, while maintaining privacy of the functions. One challenge for privacy in this setting is that the payoff and feedback of expert $i$ depends on the actions taken by her $i-1$ predecessors. This particular type of information leakage is not covered by post-processing, and new analysis is required. Our techniques for maintaining privacy with feedforward may be of independent interest.

Attribute Privacy: Framework and Mechanisms

Ensuring the privacy of training data is a growing concern since many machine learning models are trained on confidential and potentially sensitive data. Much attention has been devoted to methods for protecting individual privacy during analyses of large datasets. However in many settings, global properties of the dataset may also be sensitive (e.g., mortality rate in a hospital rather than presence of a particular patient in the dataset). In this work, we depart from individual privacy to initiate the study of attribute privacy, where a data owner is concerned about revealing sensitive properties of a whole dataset during analysis. We propose definitions to capture \emph{attribute privacy} in two relevant cases where global attributes may need to be protected: (1) properties of a specific dataset and (2) parameters of the underlying distribution from which dataset is sampled. We also provide two efficient mechanisms and one inefficient mechanism that satisfy attribute privacy for these settings. We base our results on a novel use of the Pufferfish framework to account for correlations across attributes in the data, thus addressing "the challenging problem of developing Pufferfish instantiations and algorithms for general aggregate secrets" that was left open by \cite{kifer2014pufferfish}.