Tingting Ou
Fine-Tuning Diffusion Generative Models via Rich Preference Optimization
Mar 13, 2025
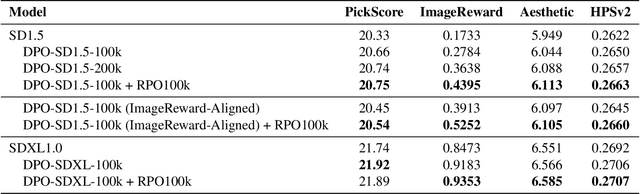
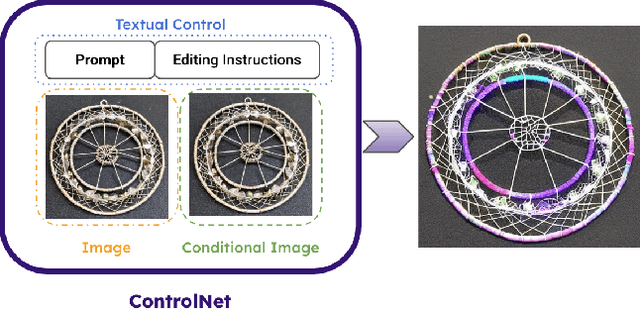
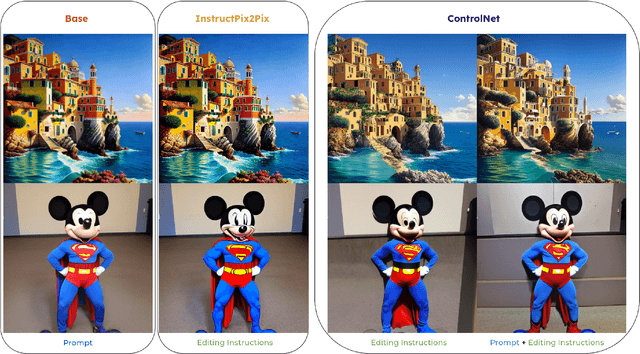
Abstract:We introduce Rich Preference Optimization (RPO), a novel pipeline that leverages rich feedback signals to improve the curation of preference pairs for fine-tuning text-to-image diffusion models. Traditional methods, like Diffusion-DPO, often rely solely on reward model labeling, which can be opaque, offer limited insights into the rationale behind preferences, and are prone to issues such as reward hacking or overfitting. In contrast, our approach begins with generating detailed critiques of synthesized images to extract reliable and actionable image editing instructions. By implementing these instructions, we create refined images, resulting in synthetic, informative preference pairs that serve as enhanced tuning datasets. We demonstrate the effectiveness of our pipeline and the resulting datasets in fine-tuning state-of-the-art diffusion models.
Thompson Sampling Itself is Differentially Private
Jul 20, 2024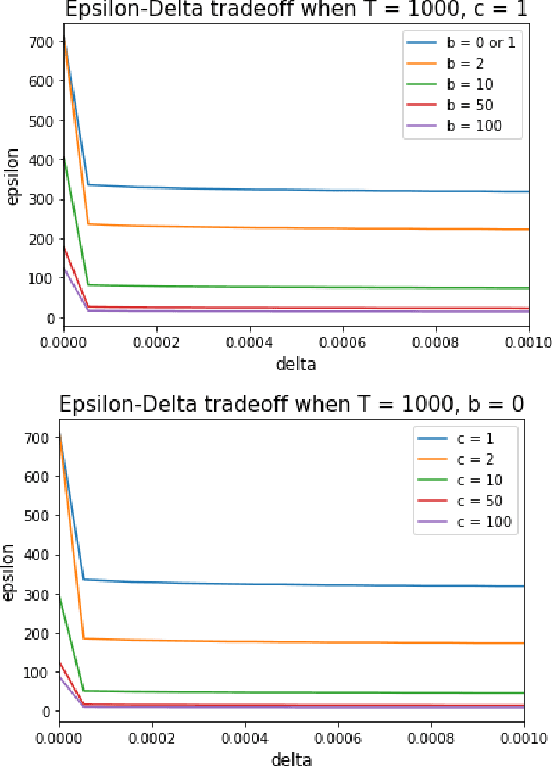
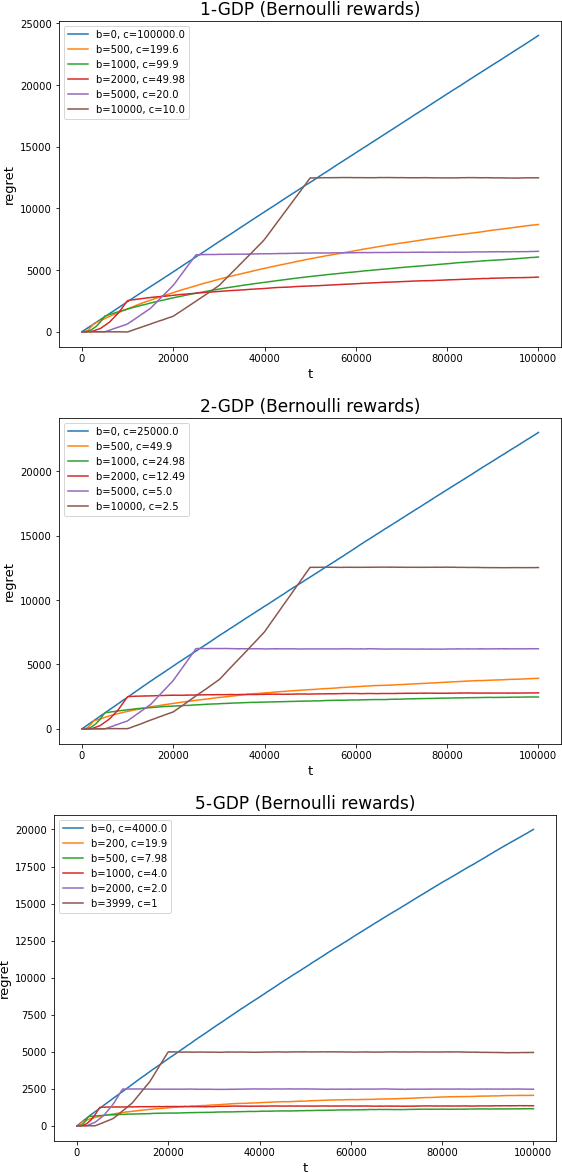
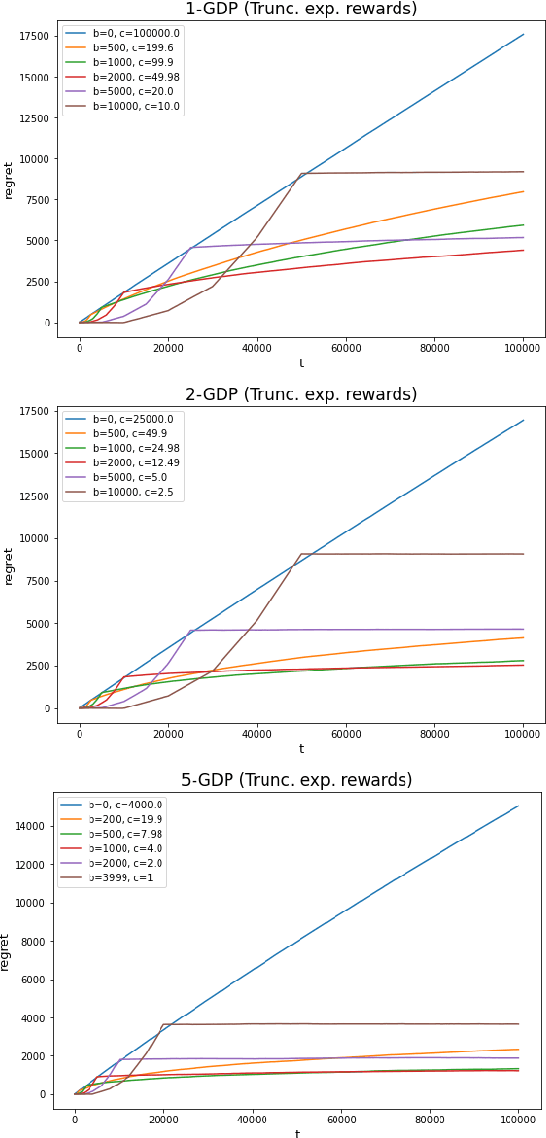
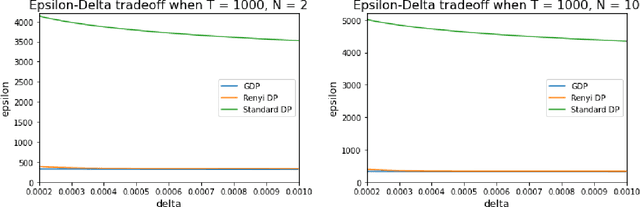
Abstract:In this work we first show that the classical Thompson sampling algorithm for multi-arm bandits is differentially private as-is, without any modification. We provide per-round privacy guarantees as a function of problem parameters and show composition over $T$ rounds; since the algorithm is unchanged, existing $O(\sqrt{NT\log N})$ regret bounds still hold and there is no loss in performance due to privacy. We then show that simple modifications -- such as pre-pulling all arms a fixed number of times, increasing the sampling variance -- can provide tighter privacy guarantees. We again provide privacy guarantees that now depend on the new parameters introduced in the modification, which allows the analyst to tune the privacy guarantee as desired. We also provide a novel regret analysis for this new algorithm, and show how the new parameters also impact expected regret. Finally, we empirically validate and illustrate our theoretical findings in two parameter regimes and demonstrate that tuning the new parameters substantially improve the privacy-regret tradeoff.
Scheduling with Speed Predictions
May 02, 2022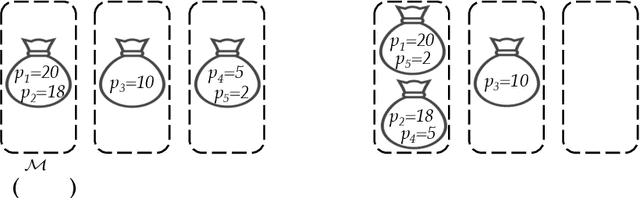
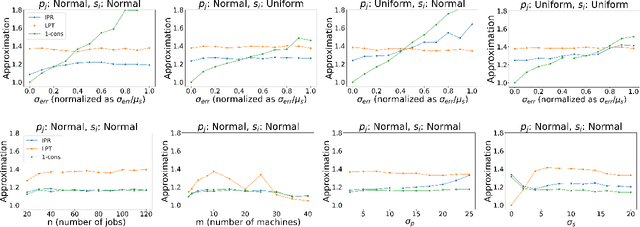
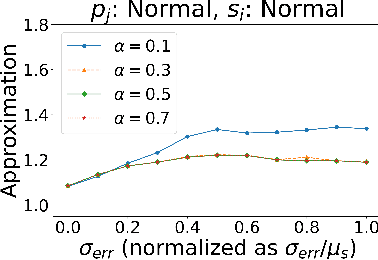
Abstract:Algorithms with predictions is a recent framework that has been used to overcome pessimistic worst-case bounds in incomplete information settings. In the context of scheduling, very recent work has leveraged machine-learned predictions to design algorithms that achieve improved approximation ratios in settings where the processing times of the jobs are initially unknown. In this paper, we study the speed-robust scheduling problem where the speeds of the machines, instead of the processing times of the jobs, are unknown and augment this problem with predictions. Our main result is an algorithm that achieves a $\min\{\eta^2(1+\epsilon)^2(1+\alpha), (1+\epsilon)(2 + 2/\alpha)\}$ approximation, for any constants $\alpha, \epsilon \in (0,1)$, where $\eta \geq 1$ is the prediction error. When the predictions are accurate, this approximation improves over the previously best known approximation of $2-1/m$ for speed-robust scheduling, where $m$ is the number of machines, while simultaneously maintaining a worst-case approximation of $(1+\epsilon)(2 + 2/\alpha)$ even when the predictions are wrong. In addition, we obtain improved approximations for the special cases of equal and infinitesimal job sizes, and we complement our algorithmic results with lower bounds. Finally, we empirically evaluate our algorithm against existing algorithms for speed-robust scheduling.
Automating Artifact Detection in Video Games
Nov 30, 2020


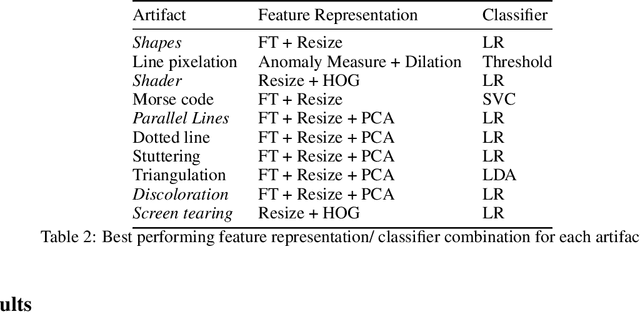
Abstract:In spite of advances in gaming hardware and software, gameplay is often tainted with graphics errors, glitches, and screen artifacts. This proof of concept study presents a machine learning approach for automated detection of graphics corruptions in video games. Based on a sample of representative screen corruption examples, the model was able to identify 10 of the most commonly occurring screen artifacts with reasonable accuracy. Feature representation of the data included discrete Fourier transforms, histograms of oriented gradients, and graph Laplacians. Various combinations of these features were used to train machine learning models that identify individual classes of graphics corruptions and that later were assembled into a single mixed experts "ensemble" classifier. The ensemble classifier was tested on heldout test sets, and produced an accuracy of 84% on the games it had seen before, and 69% on games it had never seen before.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge