An Estimator for the Sensitivity to Perturbations of Deep Neural Networks

For Deep Neural Networks (DNNs) to become useful in safety-critical applications, such as self-driving cars and disease diagnosis, they must be stable to perturbations in input and model parameters. Characterizing the sensitivity of a DNN to perturbations is necessary to determine minimal bit-width precision that may be used to safely represent the network. However, no general result exists that is capable of predicting the sensitivity of a given DNN to round-off error, noise, or other perturbations in input. This paper derives an estimator that can predict such quantities. The estimator is derived via inequalities and matrix norms, and the resulting quantity is roughly analogous to a condition number for the entire neural network. An approximation of the estimator is tested on two Convolutional Neural Networks, AlexNet and VGG-19, using the ImageNet dataset. For each of these networks, the tightness of the estimator is explored via random perturbations and adversarial attacks.

NUNet: Deep Learning for Non-Uniform Super-Resolution of Turbulent Flows

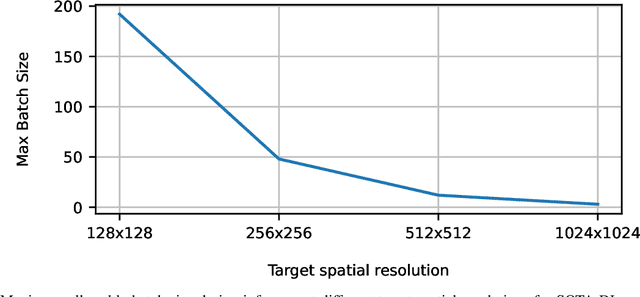
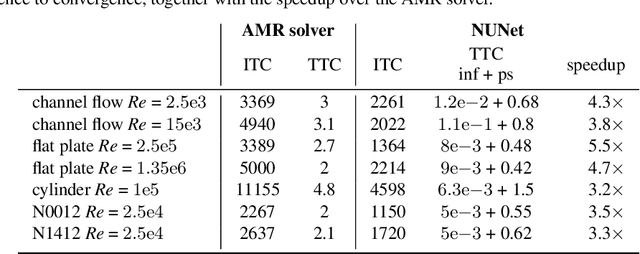
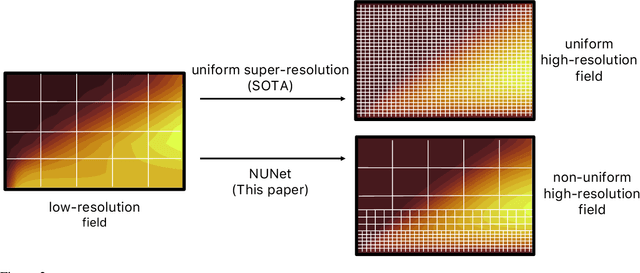
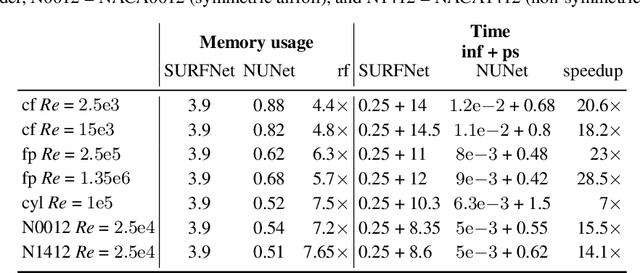
Deep Learning (DL) algorithms are becoming increasingly popular for the reconstruction of high-resolution turbulent flows (aka super-resolution). However, current DL approaches perform spatially uniform super-resolution - a key performance limiter for scalability of DL-based surrogates for Computational Fluid Dynamics (CFD). To address the above challenge, we introduce NUNet, a deep learning-based adaptive mesh refinement (AMR) framework for non-uniform super-resolution of turbulent flows. NUNet divides the input low-resolution flow field into patches, scores each patch, and predicts their target resolution. As a result, it outputs a spatially non-uniform flow field, adaptively refining regions of the fluid domain to achieve the target accuracy. We train NUNet with Reynolds-Averaged Navier-Stokes (RANS) solutions from three different canonical flows, namely turbulent channel flow, flat plate, and flow around ellipses. NUNet shows remarkable discerning properties, refining areas with complex flow features, such as near-wall domains and the wake region in flow around solid bodies, while leaving areas with smooth variations (such as the freestream) in the low-precision range. Hence, NUNet demonstrates an excellent qualitative and quantitative alignment with the traditional OpenFOAM AMR solver. Moreover, it reaches the same convergence guarantees as the AMR solver while accelerating it by 3.2-5.5x, including unseen-during-training geometries and boundary conditions, demonstrating its generalization capacities. Due to NUNet's ability to super-resolve only regions of interest, it predicts the same target 1024x1024 spatial resolution 7-28.5x faster than state-of-the-art DL methods and reduces the memory usage by 4.4-7.65x, showcasing improved scalability.

SURFNet: Super-resolution of Turbulent Flows with Transfer Learning using Small Datasets

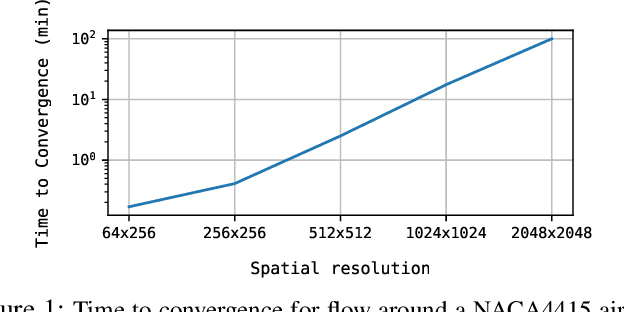
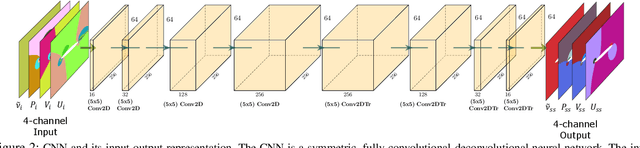
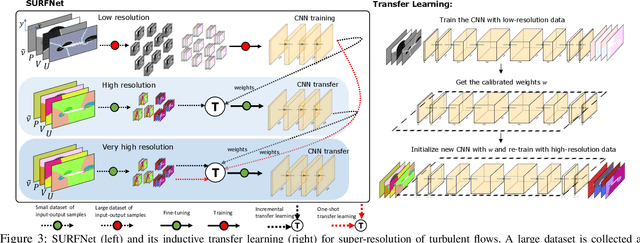
Deep Learning (DL) algorithms are emerging as a key alternative to computationally expensive CFD simulations. However, state-of-the-art DL approaches require large and high-resolution training data to learn accurate models. The size and availability of such datasets are a major limitation for the development of next-generation data-driven surrogate models for turbulent flows. This paper introduces SURFNet, a transfer learning-based super-resolution flow network. SURFNet primarily trains the DL model on low-resolution datasets and transfer learns the model on a handful of high-resolution flow problems - accelerating the traditional numerical solver independent of the input size. We propose two approaches to transfer learning for the task of super-resolution, namely one-shot and incremental learning. Both approaches entail transfer learning on only one geometry to account for fine-grid flow fields requiring 15x less training data on high-resolution inputs compared to the tiny resolution (64x256) of the coarse model, significantly reducing the time for both data collection and training. We empirically evaluate SURFNet's performance by solving the Navier-Stokes equations in the turbulent regime on input resolutions up to 256x larger than the coarse model. On four test geometries and eight flow configurations unseen during training, we observe a consistent 2-2.1x speedup over the OpenFOAM physics solver independent of the test geometry and the resolution size (up to 2048x2048), demonstrating both resolution-invariance and generalization capabilities. Our approach addresses the challenge of reconstructing high-resolution solutions from coarse grid models trained using low-resolution inputs (super-resolution) without loss of accuracy and requiring limited computational resources.

Automating Artifact Detection in Video Games

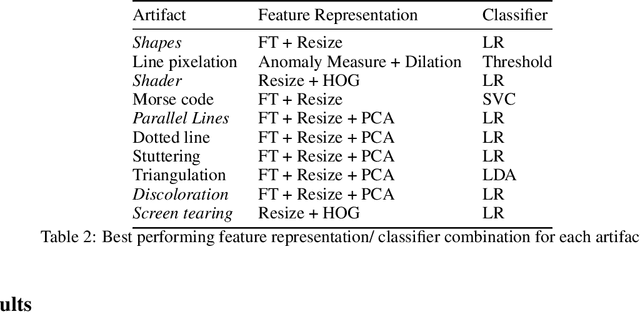
In spite of advances in gaming hardware and software, gameplay is often tainted with graphics errors, glitches, and screen artifacts. This proof of concept study presents a machine learning approach for automated detection of graphics corruptions in video games. Based on a sample of representative screen corruption examples, the model was able to identify 10 of the most commonly occurring screen artifacts with reasonable accuracy. Feature representation of the data included discrete Fourier transforms, histograms of oriented gradients, and graph Laplacians. Various combinations of these features were used to train machine learning models that identify individual classes of graphics corruptions and that later were assembled into a single mixed experts "ensemble" classifier. The ensemble classifier was tested on heldout test sets, and produced an accuracy of 84% on the games it had seen before, and 69% on games it had never seen before.

CFDNet: a deep learning-based accelerator for fluid simulations

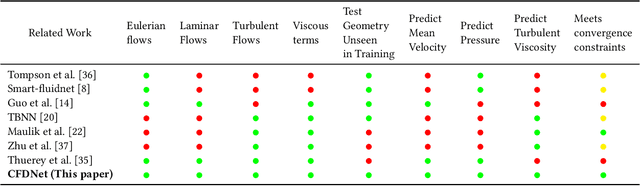
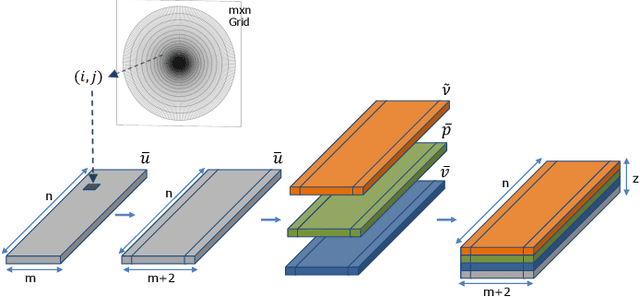
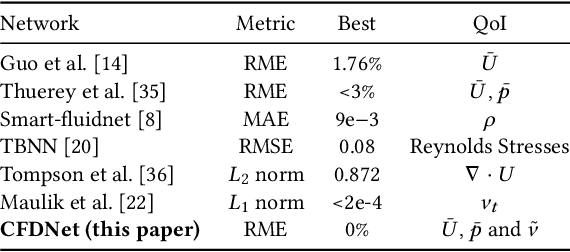
CFD is widely used in physical system design and optimization, where it is used to predict engineering quantities of interest, such as the lift on a plane wing or the drag on a motor vehicle. However, many systems of interest are prohibitively expensive for design optimization, due to the expense of evaluating CFD simulations. To render the computation tractable, reduced-order or surrogate models are used to accelerate simulations while respecting the convergence constraints provided by the higher-fidelity solution. This paper introduces CFDNet -- a physical simulation and deep learning coupled framework, for accelerating the convergence of Reynolds Averaged Navier-Stokes simulations. CFDNet is designed to predict the primary physical properties of the fluid including velocity, pressure, and eddy viscosity using a single convolutional neural network at its core. We evaluate CFDNet on a variety of use-cases, both extrapolative and interpolative, where test geometries are observed/not-observed during training. Our results show that CFDNet meets the convergence constraints of the domain-specific physics solver while outperforming it by 1.9 - 7.4x on both steady laminar and turbulent flows. Moreover, we demonstrate the generalization capacity of CFDNet by testing its prediction on new geometries unseen during training. In this case, the approach meets the CFD convergence criterion while still providing significant speedups over traditional domain-only models.