An Estimator for the Sensitivity to Perturbations of Deep Neural Networks

For Deep Neural Networks (DNNs) to become useful in safety-critical applications, such as self-driving cars and disease diagnosis, they must be stable to perturbations in input and model parameters. Characterizing the sensitivity of a DNN to perturbations is necessary to determine minimal bit-width precision that may be used to safely represent the network. However, no general result exists that is capable of predicting the sensitivity of a given DNN to round-off error, noise, or other perturbations in input. This paper derives an estimator that can predict such quantities. The estimator is derived via inequalities and matrix norms, and the resulting quantity is roughly analogous to a condition number for the entire neural network. An approximation of the estimator is tested on two Convolutional Neural Networks, AlexNet and VGG-19, using the ImageNet dataset. For each of these networks, the tightness of the estimator is explored via random perturbations and adversarial attacks.

Dynamic Temporal Reconciliation by Reinforcement learning

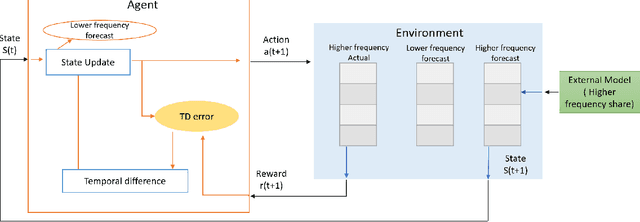
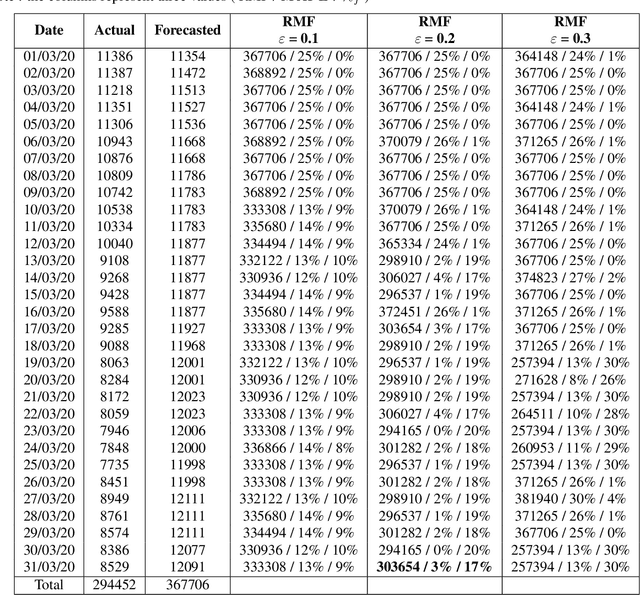
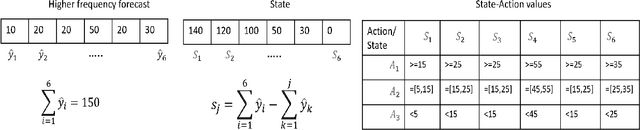
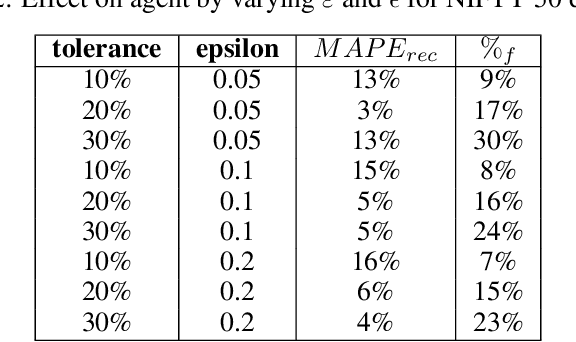
Planning based on long and short term time series forecasts is a common practice across many industries. In this context, temporal aggregation and reconciliation techniques have been useful in improving forecasts, reducing model uncertainty, and providing a coherent forecast across different time horizons. However, an underlying assumption spanning all these techniques is the complete availability of data across all levels of the temporal hierarchy, while this offers mathematical convenience but most of the time low frequency data is partially completed and it is not available while forecasting. On the other hand, high frequency data can significantly change in a scenario like the COVID pandemic and this change can be used to improve forecasts that will otherwise significantly diverge from long term actuals. We propose a dynamic reconciliation method whereby we formulate the problem of informing low frequency forecasts based on high frequency actuals as a Markov Decision Process (MDP) allowing for the fact that we do not have complete information about the dynamics of the process. This allows us to have the best long term estimates based on the most recent data available even if the low frequency cycles have only been partially completed. The MDP has been solved using a Time Differenced Reinforcement learning (TDRL) approach with customizable actions and improves the long terms forecasts dramatically as compared to relying solely on historical low frequency data. The result also underscores the fact that while low frequency forecasts can improve the high frequency forecasts as mentioned in the temporal reconciliation literature (based on the assumption that low frequency forecasts have lower noise to signal ratio) the high frequency forecasts can also be used to inform the low frequency forecasts.

Optimal Latent Space Forecasting for Large Collections of Short Time Series Using Temporal Matrix Factorization

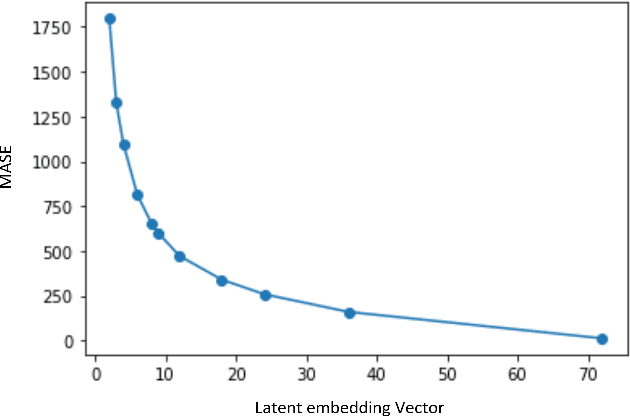
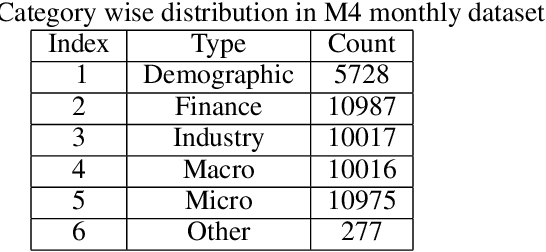
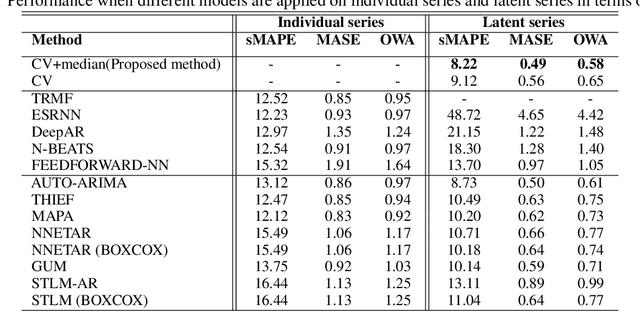
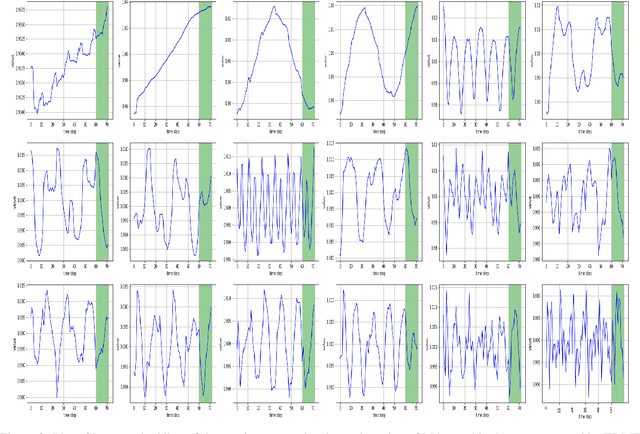
In the context of time series forecasting, it is a common practice to evaluate multiple methods and choose one of these methods or an ensemble for producing the best forecasts. However, choosing among different ensembles over multiple methods remains a challenging task that undergoes a combinatorial explosion as the number of methods increases. In the context of demand forecasting or revenue forecasting, this challenge is further exacerbated by a large number of time series as well as limited historical data points available due to changing business context. Although deep learning forecasting methods aim to simultaneously forecast large collections of time series, they become challenging to apply in such scenarios due to the limited history available and might not yield desirable results. We propose a framework for forecasting short high-dimensional time series data by combining low-rank temporal matrix factorization and optimal model selection on latent time series using cross-validation. We demonstrate that forecasting the latent factors leads to significant performance gains as compared to directly applying different uni-variate models on time series. Performance has been validated on a truncated version of the M4 monthly dataset which contains time series data from multiple domains showing the general applicability of the method. Moreover, it is amenable to incorporating the analyst view of the future owing to the low number of latent factors which is usually impractical when applying forecasting methods directly to high dimensional datasets.