Predictive Inference in Multi-environment Scenarios

We address the challenge of constructing valid confidence intervals and sets in problems of prediction across multiple environments. We investigate two types of coverage suitable for these problems, extending the jackknife and split-conformal methods to show how to obtain distribution-free coverage in such non-traditional, hierarchical data-generating scenarios. Our contributions also include extensions for settings with non-real-valued responses and a theory of consistency for predictive inference in these general problems. We demonstrate a novel resizing method to adapt to problem difficulty, which applies both to existing approaches for predictive inference with hierarchical data and the methods we develop; this reduces prediction set sizes using limited information from the test environment, a key to the methods' practical performance, which we evaluate through neurochemical sensing and species classification datasets.

A New Central Limit Theorem for the Augmented IPW Estimator: Variance Inflation, Cross-Fit Covariance and Beyond

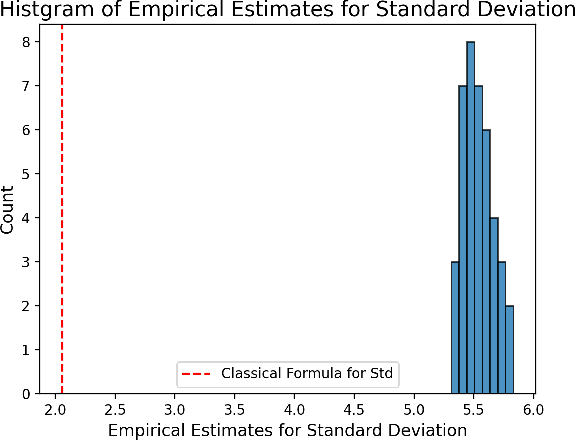
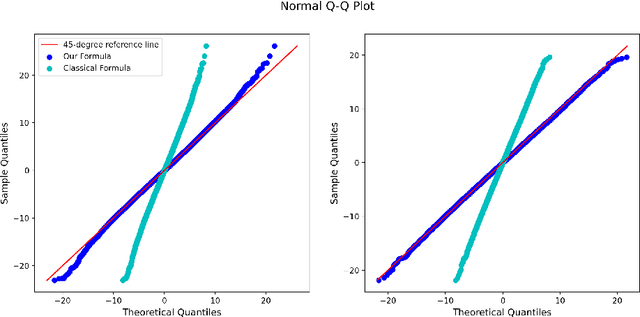
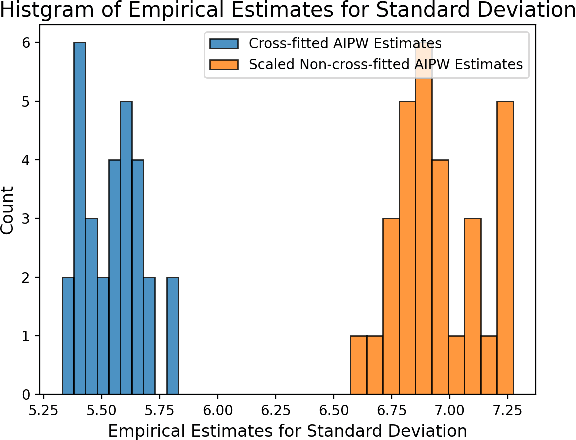
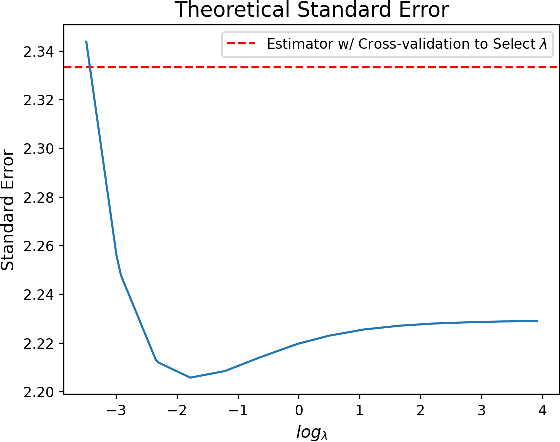
Estimation of the average treatment effect (ATE) is a central problem in causal inference. In recent times, inference for the ATE in the presence of high-dimensional covariates has been extensively studied. Among the diverse approaches that have been proposed, augmented inverse probability weighting (AIPW) with cross-fitting has emerged as a popular choice in practice. In this work, we study this cross-fit AIPW estimator under well-specified outcome regression and propensity score models in a high-dimensional regime where the number of features and samples are both large and comparable. Under assumptions on the covariate distribution, we establish a new CLT for the suitably scaled cross-fit AIPW that applies without any sparsity assumptions on the underlying high-dimensional parameters. Our CLT uncovers two crucial phenomena among others: (i) the AIPW exhibits a substantial variance inflation that can be precisely quantified in terms of the signal-to-noise ratio and other problem parameters, (ii) the asymptotic covariance between the pre-cross-fit estimates is non-negligible even on the root-n scale. In fact, these cross-covariances turn out to be negative in our setting. These findings are strikingly different from their classical counterparts. On the technical front, our work utilizes a novel interplay between three distinct tools--approximate message passing theory, the theory of deterministic equivalents, and the leave-one-out approach. We believe our proof techniques should be useful for analyzing other two-stage estimators in this high-dimensional regime. Finally, we complement our theoretical results with simulations that demonstrate both the finite sample efficacy of our CLT and its robustness to our assumptions.

Automating Artifact Detection in Video Games

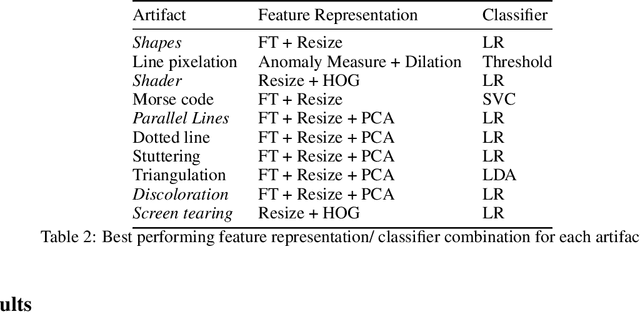
In spite of advances in gaming hardware and software, gameplay is often tainted with graphics errors, glitches, and screen artifacts. This proof of concept study presents a machine learning approach for automated detection of graphics corruptions in video games. Based on a sample of representative screen corruption examples, the model was able to identify 10 of the most commonly occurring screen artifacts with reasonable accuracy. Feature representation of the data included discrete Fourier transforms, histograms of oriented gradients, and graph Laplacians. Various combinations of these features were used to train machine learning models that identify individual classes of graphics corruptions and that later were assembled into a single mixed experts "ensemble" classifier. The ensemble classifier was tested on heldout test sets, and produced an accuracy of 84% on the games it had seen before, and 69% on games it had never seen before.